(A new question of the week)
A couple recent questions centered around how to interpret probability problems, whose wording can often be subtle, and whose solutions require care.
A dice problem about the maximum
Around the start of December, Drey sent us two questions. The first was about dice:
Hello. I have this problem:
Two dices are rolled simultaneously. Calculate the probability that the maximum is greater than or equal to 3.
Solution: 8/9
So I found that the total of outcomes is given by 6*6 since there are two dices.
Now what confuses me is the number of favorable outcomes that the exercise asks for, I tried with all of the combinations of dices greater and equal to 3 but it isn’t the solution. Can you help me please.
(Incidentally, we often see students, native English speakers or not, confusing the word “dice”. That word is a plural, not a singular, and should be thought of as if it were “dies”. The singular is “die”. So you roll one die, or two dice. For the rest of this post, I will quietly correct such minor errors, as it was never brought out in the discussion, but it is worth pointing out once.)
Problems about dice often involve the sums of the numbers showing; this is about the maximum, which has a very different feel. Drey is calculating the probability as $$\frac{\text{number of equally likely favorable outcomes}}{\text{total number of equally likely outcomes}}$$ where “favorable” means that the maximum of the number on the dice is at least 3. He correctly found the denominator, as there are 6 possibilities for the first die, and 6 for the second, so a total of \(6\times 6=36\). But what should the numerator be? It isn’t quite clear what Drey used, so we have to ask.
Doctor Fenton answered:
Hi Drey,
You haven’t said what answer you got when you tried to solve the problem, other than you did not get 8/9, so I can’t tell what you are doing incorrectly. If you want to give your answer and your reasoning, I can try to figure out why you are not getting the answer. Did you write out the possibilities and just count, or did you figure out the number of favorable outcomes by just reasoning?
Listing outcomes
The more you tell us, the more quickly we can diagnose your difficulty. In this case, it would not be hard to list the 36 possible outcomes in a table and literally count those that are favorable, which can be very helpful in understanding a problem; reasoning is more useful when you need to be able to extend it to larger problems (such as more dice). Let’s make that table:
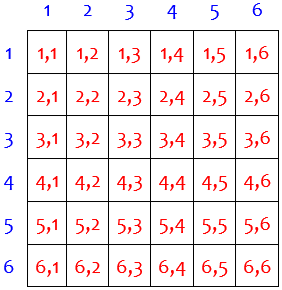
The event we are interested in is that the maximum of the two dice is at least 3. How many of these 36 possible outcomes fit that description? It’s easy, except that we have to correctly interpret the word “maximum”; we’ll do that below.
Using the complement
But how about the reasoning we would need if we don’t make the table? One counting trick that is often helpful (especially when numbers get large) is to use the complement. Doctor Fenton had more to add:
I will point that if an event has two possible outcomes which are exhaustive (that is, one of the two other outcomes must occur) and exclusive (both outcomes cannot occur at the same time), then the sum of the two probabilities must be 1. If A is the event that the maximum number on one of the dice is 3 or more, what is the complementary event that A does not happen? That is, if the maximum of the two numbers showing on the dice is not 3 or more, what can you say about the numbers showing on that roll?
Complements can be hard to think clearly about, especially if you focus too much on the words and not enough on the meaning. But once you are over that hurdle, the thinking can become easier. To help with that, Doctor Fenton offered a different problem (the more common question about sums, but with three dice so it is considerably harder to make a table) to illustrate:
It is often easier to find the probability that an event does not occur than to find the probability that the event occurs directly. For example, if you roll three dice, what is the probability that the sum of the numbers showing will be 5 or more? Now there are 63 = 216 outcomes, and most of them will be favorable. If you write out all the possibilities, that will be a lot to count. But if this event (sum ≥ 5) does not occur, then the sum must be 4 or less. The smallest possible sum is 3, with each die showing a 1, and if one die shows a 3 or higher, or if two dice show 2, then the sum must be at least 5. The only outcomes for which the sum is less than 5 are outcomes for which the sum is 3 or 4. That happens if all three dice show 1, or two dice show 1 and the third die shows 2. That is 4 possibilities, so the probability P(sum<5) is 4/216=1/54. Therefore, the probability P(sum≥5) must be 1-(1/54) = 53/54. Do you see how it can be much easier to count the complementary event than to count the event directly?
In this example, the complementary event can be easily listed: \({(1,1,1), (1,1,2), (1,2,1), (2,1,1)}\), so we know there are 4 outcomes, and therefore \(216-4=212\) outcomes in the event we are interested in.
Drey responded,
Hello Doctor Fenton.
I apologise for not showing my answer to the problem.
I followed your advice and tried to use the complementary event formula in which P(A)+P(B)=1.
Since we have the 2 dice, then the total number of outcomes will be 6^2=36.
Now for the favorable number of events, since we are looking that the event doesn’t occur (where the dice need to be less than 3 (P(B)<3)) I managed to count only one event where each die is showing 1: {1,1}. Now using the formula of the complementary event we have that P(A) + 1/36 = 1 ==> P(A) = 1 – 1/36 ==> P(A) = 35/36.
That is the result I got. Please correct me where is needed.
I anxiously await your response.
Drey’s notation “P(B)<3” is confusing; taken literally, it means that the probability of the complementary event is less than 3. He may mean the probability that the sum of the numbers on the dice is less than 3, as that is a way to describe the complementary set he is counting:
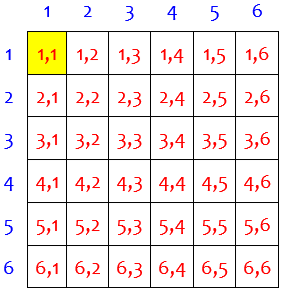
So the probability he found is for this event, which could be described as “sum < 3”, or as “both < 2”:
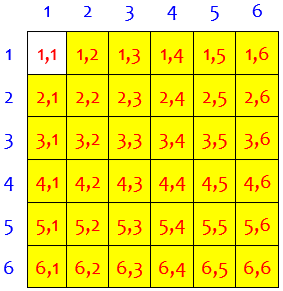
Doctor Fenton replied, trying to clarify what the event and its complement are:
That’s a good start, but you haven’t correctly identified the complementary event. The original event was that the maximum number showing is 3 or more. There is more than one event, (1,1), where the maximum showing is not at least 3. What is the maximum number which can occur in the roll, and how many outcomes does that describe?
The missing piece is to identify the event correctly; the language is difficult. If the maximum of the two numbers is not at least 3, then it is less than 3; in which outcomes is the maximum less than 3?
Understanding the problem
Drey said,
Doctor Fenton, I apologise but I require some further explanation. You are correct I am having trouble identifying the complementary event.
If the problem says that the maximum number of the 2 dice rolled is 3 or greater, shouldn’t the complement be the results that are not 3 or greater (< 3)? and since if one die is 2 and the other is 1 then the result is not part of the complement since it shouldn’t be equal to 3.
It’s true that the complement of “3 or greater” is “less than 3”. But the key word is “maximum”, which Drey doesn’t use here. My guess is that Drey has let that word get tangled up in the “greater than” and lost it, changing the event from “the maximum is greater than or equal to 3” to something like “it is greater than or equal to 3”, and taking it to be about the sum. (Another easy misreading would be something like “the numbers are both greater than or equal to 3”.)
Eight minutes later, Doctor Rick joined in, having been following the discussion:
Hi, Drey. I know Doctor Fenton could answer, but I’d like to respond to you quickly.
I believe you have been misreading the problem. It is easy to do: the first time I read the problem, I assumed that it meant to say that the sum is greater than or equal to 3, because that is a common type of problem with dice. But it means what it says: The maximum of the numbers on the two dice is greater than or equal to 3. If one die shows a 1 and the other shows a 2, then the maximum of those two numbers is 2, which is less than 3!
Does this change your answer?
All he has done here is to point out the word “maximum”, and expand it to “The maximum of the numbers on the two dice” to make it stand out. And giving a simple example is often a good way to make the meaning of a complicated statement clear.
Getting it right
Drey replied,
Hello Doctor Rick.
I managed to understand what the question is asking for, thank you.
So I managed to get 4 possible outcomes if I am following your explanation correctly: {1,1; 1,2; 2,1; 2,2}. Using the complementary event formula I got that: p(a)=1 – 4/36 ==> 32/36 ==> 8/9
Doctor Fenton.
Thank you very much. I managed to solve the exercise but also for the insight on how to solve it using the complementary event formula.
To which Doctor Fenton replied,
You’re welcome! Glad we could help.
Here is the complementary event, in which the largest of the two numbers is less than 3:
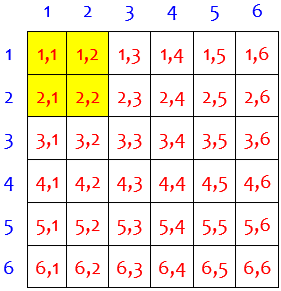
Without listing, that could be counted by seeing it as “both numbers are less than 3″, so that there are 2 choices for the first and 2 for the second, making a total of \(2\times 2=4\). So the probability of the complement is \(\frac{4}{36}=\frac{1}{9}\). The probability of the event itself is \(1-\frac{1}{9}=\frac{8}{9}\). Or, without simplifying first, seeing it as Drey did, the event consists of \(36-4=32\) outcomes:
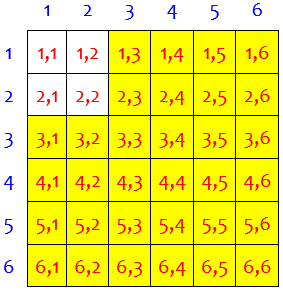
This could have been counted directly as “first die is at least 3, or second die is at least 3″; but every way to do that with formulas is considerably longer. One way is to use the formula $$P(A\text{ or }B)=P(A)+P(B)-P(A\text{ and }B)$$ applied to$$P((\text{first }\ge 3)\text{ or }(\text{second }\ge 3))=\frac{4}{6}+\frac{4}{6}-\frac{4}{6}\cdot\frac{4}{6}\\ =\frac{24}{36}+\frac{24}{36}-\frac{16}{36}=\frac{32}{36}=\frac{8}{9}$$ This formula amounts to adding the red- and green-bordered regions, then subtracting their overlap:
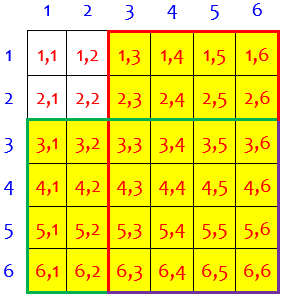
Another is to use $$P((\text{first }\ge 3\text)\text{ or }(\text{first }< 3\text{ and second }\ge 3))\\ =\frac{4}{6}+\frac{2}{6}\cdot\frac{4}{6}\\ =\frac{24}{36}+\frac{8}{36}=\frac{32}{36}=\frac{8}{9}$$
This amounts to adding the green and the yellow regions here:
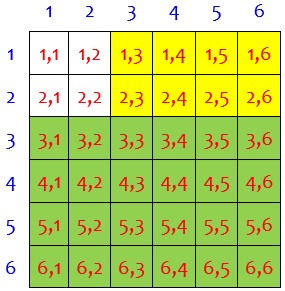
A ball-and-urn problem
Besides dice and cards, the most standard sort of probability problem involves colored or numbered balls in an “urn”. (Probably most of us never encounter urns any more except in such problems!) The following day, Drey asked about one of those:
Greeting, I have this exercise of probability that is a little confusing to me.
Here’s the exercise: One urn contains 4 white balls, 4 black balls and 4 red balls. 6 balls are removed from that urn. Determine the probability of 2 balls of each color being drawn.
(A) Assuming extraction with replacement
Solution = 1/8
(B) Assuming extraction without replacement
Solution = 2/77
What I tried to do: (A) as this line says that 2 balls are removed with replacement, so there is no need to apply simple combination. Total number of outcomes = 12, number of events are two balls of each color, and since each draw is an independent event, I can multiply the probability to draw a red ball on the first serve, a red ball on the second serve, a black ball on the third serve, a black ball on the fourth serve withdraw; a white ball in the fifth and a white ball in the sixth. That is: p = 4/12 * 4/12 * 4/12 * 4/12 * 4/12 * 4/12 = 4096/2985984 = 1/729 which is wrong.
For line (B) I have to apply simple combination because there is no replacement where number of events C6.2 = 360 and C12.6 for the total number of events we have that p = 360/924 = 30/77 Could You please help me? Your time is appreciated, I await your response. Thank you.
This is a model of the way we like to see questions asked: stating the entire problem, including the provided solutions (which lets us check whether the student is confused only because their book gave a wrong answer!), and a careful explanation of his own thinking.
With and without replacement
In the case of selection with replacement (putting a ball back after it’s been looked at), each selection is independent, and the probabilities are the same each time. Drey therefore multiplied the probability of each ball having the appropriate color in order, two reds, two blacks, two whites, each probability being the same because there are 4 of the given color out of 12 at each selection. There’s only a small error there.
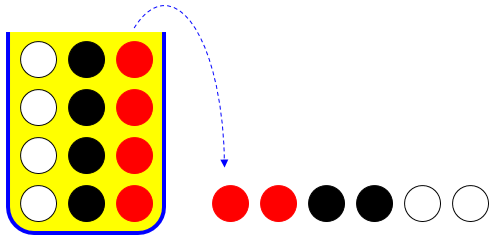
In selection without replacement (so that after each draw there is one less ball, and the probabilities change), Drey (wisely) chose to use combinations. His notation “C6.2” means what is more commonly written as “\({6\choose 2}\)” or “\(_6C_2\)” or “\(C(6,2)\)”. He found the total number of ways to choose 2 of the 6 balls, and divided by the total number of ways to choose 6 of the 10 balls. This, too has an error.
Identifying the errors
I answered:
Hi, Drey.
Your work for the first part would be good if you were only asked for the probability of drawing balls in the order RRBBWW. What more needs to be done because the order doesn’t matter? (I would also simplify before multiplying, making the arithmetic a lot easier!)
The error here is simple: “Two of each color” does not require selection in any particular order; and the multiplication he did gives only the probability that the first two are red, the second two are red, the third two are black, and so on. The fix will be easy.
For the second part, the numerator will not be C(6, 2); you are not just choosing 2 of 6. Can you explain your thinking there more fully? You may just need a small change in your approach.
My best explanation of Drey’s thinking is that he pictured the results sitting in a row of 6, and wanted those results to include two reds, so he counted ways to choose 2 of the 6 places to be red. He just forgot the other colors.
There are typically many ways to solve a combinatoric problem like this, though, so I didn’t want to presume that he was necessarily thinking that way.
I have to say that I don’t get answers of 1/8 and 2/77 as you appear to be saying you were told. I get something very close to the first, and considerably more for the second. (I have held off on answering you while I keep returning to the problem to look for an error in my own work; if another of us does get those answers, they may join me in helping!)
I had to take the time to convince myself that my thinking was right even though it led to different answers than the book, before deciding to try to help!
Getting it right
Drey replied,
Hello Doctor Peterson.
Well since the order doesn’t matter we have to pick the number of ways that these 6 colours can be rearranged, coincidentally that is a permutation with repetition where C6,2,2,2 = 6!/2!*2!*2 = 90 so since this is part of the event I multiplied it by 1/729 meaning: 1/729*90 = 90/729 = 10/81
This is what was needed to correct the undercount. He previously counted the probability of choosing RRBBWW in that order as \(\frac{4^6}{12^6} = \frac{1}{729}\); he multiplied that by the number of ways to rearrange these to obtain all possible “successful” selections, namely the number of ways to arrange the letters RRBBWW. This is \(\frac{6!}{2!2!2!} = 90\). The product, \(\frac{10}{81}\), is very close to the supplied answer of \(\frac{1}{8}\), but not quite.
For the second part(B) I managed to find the same problem in a few websites and most of them suggest that the answer is wrong, They did this:
C12,6 = 12!/6!*6! = 924 (total number of outcomes)
Total of combinations for 2 white balls
C4,2 = 4/2!*2! = 6
Total of combinations for 2 black balls
C4,2 = 4/2!*2! = 6
Total of combinations for 2 red balls
C4,2 = 4/2!*2! = 6
P = (C4,2*C4,2*C4,2)/C12,6 = 6^3/924 = 18/77
The denominator will be the number of ways to choose 6 of 12 balls, $${{12}\choose{6}} = \frac{12!}{6!6!} = \frac{12\cdot11\cdot10\cdot9\cdot8\cdot7}{6\cdot5\cdot4\cdot3\cdot2\cdot1}=924$$
The numerator has to be the number of ways to choose 2 of the 4 white, 2 of the 4 black, and 2 of the 4 red, for a total of \({{4}\choose{2}}\cdot{{4}\choose{2}}\cdot{{4}\choose{2}}=6\cdot6\cdot 6 = 216\), so the probability is \(\frac{216}{924} = \frac{18}{77}\). This is 9 times as much as the book’s answer of \(\frac{2}{77}\); I can’t imagine how they got this wrong.
Now what I don’t get is the thought process behind the multiplication at the last part.
Could you maybe help explain?
Thank You for Your help.
After agreeing with the two answers, I responded to the question at the end:
The numerator has to be the number of ways to choose 2 red, 2 black, and 2 white. So we have to choose 2 of the 4 red, AND 2 of the 4 black, AND 2 of the 4 white. This is the product of the three separate combinations.
Case closed.
