(A new question of the week)
We’ve looked at domain and range problems before, but some have more interesting details than others. Here is a superficially basic radical function (and the answer is extremely easy when you just use a graphing tool), which raised some interesting issues while solving it algebraically.
Domain and range: basic approaches
This question came from repeat “patient” Mubashshir in mid-January:
What is the domain and range of the function?
f(x) = 2x/√(4x-x²)
The function, written out nicely, is $$f(x) = \frac{2x}{\sqrt{4x-x^2}}$$
A bare question like this, with no indication of what particular help is needed, calls for some questioning before we can decide what most needs to be said. We need to know what tools the student has in his tool kit, and what difficulties he’s faced in using (or just choosing) them. Doctor Rick answered, mixing that request for information with a variety of suggestions:
Hi, Mubashshir.
As we have said before, we want you to show whatever work you have done, and tell us what you have been learning, so that we can see where you need help and what methods are available to you.
Finding the domain of a function is generally a straight-forward task: you just look for values of x for which the function cannot be evaluated. There are two particularly common reasons that an algebraic expression cannot be evaluated: either the denominator is zero, or there is a negative number under a square root. If you have been able to do this part of the problem, I’d like to see your answer; if you haven’t, please show me your work, so I can see how far you got and where you had difficulty.
For discussions of domain (and other issues we’ll be dealing with here), see this post:
Domain, Range, and Quadratic Inequalities
Finding the range of a function is often much harder, and a variety of methods might be needed, depending on the function.
One common technique is to find the inverse of the function; the range of a function is the domain of its inverse, and as I said, finding the domain is relatively easy. However, finding the inverse in this case is a bit more difficult, because it involves squaring both sides of an equation, and this can introduce extraneous solutions.
For more on range (including a radical function somewhat like ours here), see
Finding the Range of a Function
For examples of extraneous solutions and what to do about them, see
Extraneous Solutions: Causes and Cures
If you know calculus, you could try finding the derivative of the function. This can then be used to find relative minima and maxima of the function; and that’s a big help in finding the range. But again, there is one complication in this case (I won’t even get into that if you don’t know calculus yet).
Please show me your work, using these suggestions if they help, and tell me something about what you have learned. Then we can have further discussion about how to solve this challenging problem.
We’ll take a look at calculus when we look at the graph, and we’ll see what complicates it a little.
Looking for the inverse
Mubashshir replied, choosing the inverse function route:
I don’t know calculus.
y = f(x) = 2x/√(4x–x²)
→ 4x²+x²y² = 4xy²
I can’t do more.
Doctor Rick answered,
I didn’t think it too likely that you knew calculus, though one of your past questions was on a topic somewhat related to calculus (sums of series). So we will put that tool aside.
You didn’t say how you did on finding the domain, but you showed some initial work on my first suggestion for finding the range. As a first step to inverting the function, you wrote
y = 2x/√(4x–x2)
4x2 + x2y2 = 4xy2
Presumably what he has done here is to multiply both sides by the denominator, and square both sides:
$$y=\frac{2x}{\sqrt{4x-x^2}}\\ y\sqrt{4x-x^2}=2x\\ (y\sqrt{4x-x^2})^2=(2x)^2\\ y^2(4x-x^2)=4x^2\\ 4xy^2-x^2y^2=4x^2\\4xy^2=x^2y^2+4x^2$$
That’s good so far. Our goal here is to solve for x in terms of y, which will be (almost) the inverse function, x = f –1(y). So we’d like next to isolate x on one side — but we can’t really do that, because there are terms in both x and x2. One thing we could do is to think of the equation above as a quadratic equation in x, treating y (for now) as just a number.
If we did that, we’d write it as $$(y^2+4)x^2-4xy^2=0$$ and factor it: $$x((y^2+4)x-4y^2)=0$$ so that either \(x=0\) or \((y^2+4)x-4y^2=0\) which leads to $$x=\frac{4y^2}{y^2+4}$$
Or … we could notice that all the terms have a factor of x, so we can divide the equation through by x. The only problem with this is that we have to remember x can’t be 0 when we divide by it. So we consider the case x = 0 first, and we see that when x = 0, y = f(x) cannot be evaluated (so 0 is not part of the domain of f).
When x ≠ 0, we do the division and get
4x + xy2 = 4y2
which is easy to solve for x. When you have done that, the domain of this (inverse) function will be the set of values of y for which the function f –1(y) can be evaluated.
Again, we find that $$x=\frac{4y^2}{y^2+4}$$
Incidentally, you may be confused by the fact that he didn’t interchange x and y as is often taught, at least in American schools, as the first step in inverting a function. For a discussion of this, see
How to Find an Inverse Function: Conflicting Approaches
We generally defer to the method a student is using, to avoid confusing them; but in this case, as I state there, this is my preferred approach.
Now we have an inverse function (x as a function of y); what is its domain (possible values of y)?
I mentioned before that there is an issue yet to be resolved, because you obtained your equation by squaring, and this means that our new function is not exactly the inverse of f. But I’ll leave it here for now, to see what you can do with it, since I’m not even sure whether you want to continue working on the problem at all. If you do, please show me all the work you can do (even if you think it’s wrong — that would still show me important things).
Since the denominator is always positive, the domain of the inverse as we see it so far would be all real numbers.
Finding the domain
We’ll be coming back to that soon; but for the moment, Mubashshir answered by showing work for the domain of the given function:
f(x) ∈ R, 4x – x² > 0
x² – 4x < 0
Domain = (0,4)
Here he is looking at the radicand in the denominator of our function \(f(x) = \frac{2x}{\sqrt{4x-x^2}}\), which has to be non-negative in order to take the root (as a real number), and non-zero in order to divide by it. Such a polynomial inequality can be solved in several ways (which are discussed in one of the blog posts mentioned above). One way is just to sketch the graph of \(4x-x^2\):
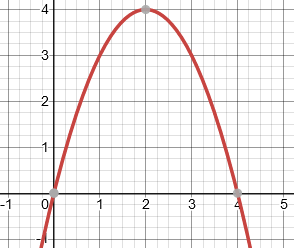
This is positive between 0 and 4.
Finding the range
Next, he returned to the range, deriving the inverse again and looking at its domain:
y = 2x/√(4x–x²)
4x + xy² = 4y²
x = 4y²/(4 + y²)
x ∈ R, 4 + y² ≠ 0
It’s not possible.
Range = {x ∈ R: x > 0}. [f(x) is always larger than 0]
If I’m not right, please tell me.
What is “not possible” is for the denominator to be zero, so that the inverse is defined for all values of y … so then, what is that next line saying?
Doctor Rick answered,
You correctly found the domain to be (0, 4). The quantity under the square root, 4x – x2, must be non-negative, yielding 0 ≤ x ≤ 4; but also the denominator, which is the square root of that quantity, cannot be zero, removing 0 and 4 from the domain. Good work on that part!
Then,
On the range, you did correctly what I suggested, and you found no values of y that could not be in the domain of x = 4y²/(4+y²). But you didn’t stop there and assert that the range is all real numbers! You stated that f(x) is always greater than 0, so the range is y > 0.
That is correct, but I am left wondering how you drew that conclusion. Could you explain your reasoning? This is the tricky part of the problem, so I don’t want to miss the opportunity for us to learn something from it.
Some subtleties of the range
After a brief side discussion, Doctor Rick repeated:
I asked you why you said that
Range = {x ∈ R: x >0}. [f(x) is always larger than 0]
Even if you can’t explain very clearly, you must have had some reason for thinking that. I can think of some possibilities, but I want to hear it from you! Whatever you can say about this will be a basis for further discussion.
Mubashshir replied,
x = 4y²/(4 + y²)
x ∈ R, iff 4 + y² ≠ 0
So, y² ≠ –4, it’s not possible. For this reason the range would be all real numbers. But we will not get any negative numbers or 0 for the values which are included as domain. The set of the values of y are range. So, the range can’t be less than 0. So, I said the range is (0,∞).
Now Doctor Rick could say more:
Thanks, Mubashshir. That is what I was looking for — and it is pretty much what I would have guessed.
We had seen that the domain of the function x = 4y²/(4 + y²) (which would be the range of f(x) if this function were truly f -1(y) ) is all real numbers. However, I suppose you noticed that with
f(x) = 2x/√(4x – x2)
when x is in (0, 4), the numerator is positive and the denominator is also positive, so f(x) must be positive. Thus the range of f must be the positive numbers or some subset of the positive numbers.
This is what Mubashshir had explicitly said. But that is not quite enough:
The only thing we haven’t established for certain is that all positive numbers are in the range. There are things we can say that are more or less in the realm of calculus, but that should at least make sense without a study of calculus. For instance, f(x) is continuous for x in (0, 4): that is, there is no sharp break in the graph of f(x). That’s because the numerator 2x is continuous (its graph is a straight line), and the denominator √(4x–x2) is also continuous (its graph is a semicircle), and the denominator is not zero between x = 0 and x = 4 (though it is zero at both those end points). We can also consider the limits of f(x) as x gets very close to 0 on the one hand, or very close to 4 on the other. It’s easy to see that for x very close to 4, the numerator is close to 8 while the denominator is a small positive number – getting even smaller as x gets closer to 4. And a fraction whose denominator is very close to zero has a very large value. As x approaches zero, though, it’s harder to be sure without formal calculus concepts.
Here is what the denominator, \(\sqrt{4x-x^2}\), looks like (the semicircle):
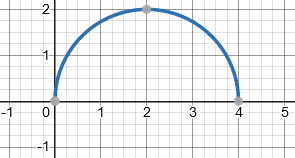
As x approaches 4, the fraction \(\frac{2x}{\sqrt{4x-x^2}}\) approaches “8/0”, that is, it becomes infinitely large; so we know that there is no upper bound. But as x approaches 0, the fraction approaches “0/0”, which is indeterminate: We can’t determine what it does without more advanced methods. In particular (keep your eyes closed if you don’t want any calculus), we find that $$\lim_{x\to 0}\frac{2x}{\sqrt{4x-x^2}}\\ = \lim_{x\to 0}\frac{2x}{\sqrt{x}\sqrt{4-x}}\\ = \lim_{x\to 0}\frac{2\sqrt{x}}{\sqrt{4-x}}\\ = \frac{0}{4} = 0$$
Another approach, probably more fruitful for you, is to consider what went wrong as we tried to find the inverse of f. As I mentioned, the problem was that we squared both sides. The work, again, was
[1] y = 2x/√(4x – x2), 0 < x < 4
[2] y2 = 4x2/(4x – x2) (squaring both sides)
[3] 4x2 + x2y2 = 4xy2
[4] 4x + xy2 = 4y2 (dividing by x, which cannot be 0)
[5] x = 4y2/(4 + y2)
From step 2 on, negative values for y are allowed. In fact, for any positive value of y, its negative will also work. Thus, x as a function of y is an “even” function – its graph is symmetric in the x axis – because replacing y by –y does not change the function.
This, again, is not the actual inverse.
Going backward now, I conclude that for any pair (x, y) that satisfies [5], the pair (x, -y) also satisfies [5], but we only want to keep the pair with positive y. Therefore I conclude that the range of [1] is (0, ∞). (One other thing I forgot to say: since we know x cannot be 0, y also cannot be 0; without this, I would have concluded that the range of [1] is [0, ∞).)
You can graph [1] and [5] to see more clearly what’s going on.
So what do the graphs say?
That was the end of the discussion. Let’s take a look at the graph of our function (equation [1]:
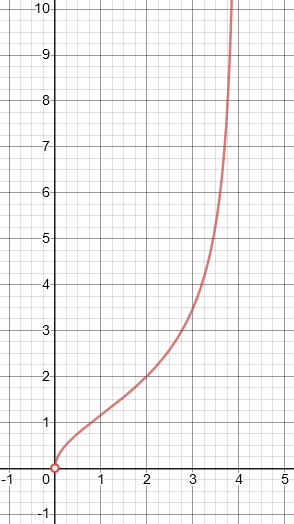
As we’ve seen, the domain is \((0,4)\), and the range is \((0,\infty)\).
And here is the graph of the equation \(4x^2 + x^2y^2 = 4xy^2\) (equation 3), or \(\displaystyle x = \frac{4y^2}{4+y^2}\) (equation [5]):
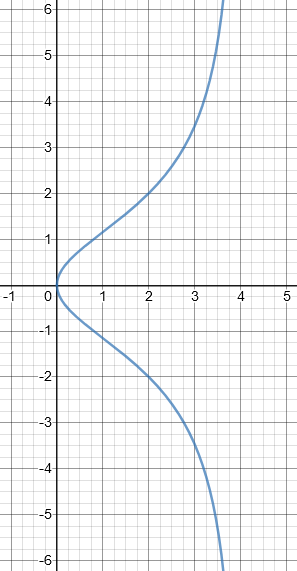
Observe that this equation includes the origin (because we are no longer dividing), and is symmetrical (because we don’t take the square root); and that here y is not a function of x.
Now, what would happen if we used calculus to find the domain? We’d first look for local maxima or minima by finding the derivative: $$f(x) = \frac{2x}{(4x-x^2)^{1/2}}\\ f'(x) = \frac{2(4x-x^2)^{1/2}-2x(4-2x)\frac{1}{2}(4x-x^2)^{-1/2}}{4x-x^2}\\ =\frac{2(4x-x^2)-x(4-2x)}{(4x-x^2)^{3/2}}\\ =\frac{8x-2x^2-4x+2x^2}{(4x-x^2)^{3/2}}\\ =\frac{4x}{(4x-x^2)^{3/2}}$$ At first glance, this will be zero only at \(x=0\); but it is actually indeterminate there. If we use the same trick we used above to find the limit, we find $$\lim_{x\to 0}\frac{4x}{(4x-x^2)^{3/2}}\\ = \lim_{x\to 0}\frac{4x}{x^{3/2}(4-x)^{3/2}}\\ = \lim_{x\to 0}\frac{4}{x^{1/2}(4-x)^{3/2}}\\ = \infty$$
The same, more simply, is true of the limit of the derivative at 4. Also, we can observe that the derivative is always positive, so the function is monotonically increasing. This agrees with our graph, and indicates that there is no minimum, and that the limits of the function determine the range.
