(A new question of the week)
We had a long discussion last August about domain and range of functions involving either quadratic functions or restricted domains (or both). Two Math Doctors got involved, offering different ways to approach the same problem. I’ve edited the discussion to avoid some intermingling of topics.
A quadratic inequality
Here is the question, from Mooija:
Hi, I tried this, but just can’t get to the right answer.
I watched a few videos to try and understand better, but it did not help.
The answer to the question is x ≥ 4 and x ≤ 3.
Please help me to find out what I’m doing wrong.
I need to find the largest possible domain of the function.
Take the time to identify any errors you see here.
Doctor Fenton replied:
You are looking at the right information, but not analyzing it correctly. You factored the quadratic correctly, and you are looking at the sign of each factor, finding the interval where each factor is non-negative.
What you are overlooking is that the sign of the quadratic is not determined by the sign of a single factor, but by the signs of all the factors.
One way to solve the problem is to note that the factor (x – 3) is positive when x > 3 and the factor (x – 4) is positive when x > 4. You can use these two points to cut the number line into three intervals: x < 3; 3 < x < 4; and x > 4. Then look at the sign of the quadratic in each interval.
x-4 < 0 x-4 < 0 x-4 > 0 x-3 < 0 x-3 > 0 x-3 > 0 --------------+------------------+------------- 3 4The product of two numbers is positive when both numbers have the same sign, and is negative when the numbers have opposite signs.
Using this fact, can you now determine the intervals where (x – 3)(x – 4) is positive? Since you want the intervals where the product is non-negative, you should include the endpoints of each interval where the quadratic is positive in your answer.
Another way to view the problem is geometric or graphical. The graph of y = (x – 3)(x – 4) is a parabola, a U-shaped curve. You are looking for the intervals where the curve is on or above the x-axis. The factorization shows that the curve crosses the x-axis at x = 3 and at x = 4. Being U-shaped (and opening upward) it descends on the left interval, crosses at x = 3 and goes below the x-axis and stays below until x = 4, and finally rises to the right of x = 4.
The solution therefore is x ≥ 4 or x ≤ 3. (Mooija had said “x ≥ 4 and x ≤ 3″, presumably meaning the union of those two sets. From what we’ll see below, this appears to be what was taught, though I consider it incorrect.)
Mooija’s specific error was to divide by a factor; we’ll see that again below.
For a similar correction of a similar error, see:
An Odd Inequality Reversal
Mooija had a further question:
Thank you that helped lots. I get it now 😀
I got another problem that is basically a continuation of this but with another question.
Can you help me with that too please?
You see what you explained for me was the domain; now I need to find the range with a given domain and I don’t know how to do that.
Doctor Fenton answered,
I mentioned that the graph of this quadratic is a parabola, which is somewhat U-shaped, so there will be a lowest point on the graph. Graphically, the range of a function is the set of all points on the y-axis which can be reached by going horizontally from a point on the graph. Once you know a point (x0, y0) on the graph, that number y0 will belong to the range, and any y-value larger than y0 will also be in the range.
In particular, if you know the y-coordinate y0 of the lowest point on the graph, the set of all y ≥ y0 will be in the range.
What do you know about finding the lowest point on a parabola y = ax2 + bx + c?
The range of \(x^2 – 7x + 12\), which can be rewritten as \(\left(x – \frac{7}{2}\right)^2 – \frac{1}{4}\), is \(x \ge -\frac{1}{4}\). This turns out not to be needed …
The context: domain of a radical function
Doctor Rick jumped in, having seen a missing aspect of the problem:
Hi, Mooija, I’d like to add something to what Dr. Fenton has said, because I’m not sure we have really answered the question. I’d like to see exactly what the question asked!
You gave an inequality,
x2 – 7x + 12 ≥ 0
You showed the “answer to the question” as “x ≥ 4 and x ≤ 3”, which tells me that the “question” is to solve the inequality. But then you added, “I also need to find the largest possible domain of the function.” Can you tell us what function that is talking about?
If it’s the function
f(x) = x2 – 7x + 12
then the largest possible domain of f is not what you discussed with Dr. Fenton, but rather the set of all real numbers. This question has nothing to do with whether f(x) is positive or negative, only with whether f(x) can be evaluated.
Now, if the problem was dealing with the function
g(x) = √ f(x)
= √(x2 – 7x + 12)
then you’ve done the right thing in determining the interval(s) on which f(x) ≥ 0. I just can’t be sure that this is what you’re doing, because you haven’t told us. That’s why I hope that you will clarify what the problem actually says.
Mooija replied:
Okay now to clarify I asked for help with question 7g. This is straight out of my textbook now:
Solutions:
Doctor Rick had made the right guess! He responded,
Thanks, Mooija, that answers my question! You were finding the greatest possible domain of the function
f(x) = √(x2 – 7x + 12)
so you did exactly the right thing when you solved the inequality asserting that the quantity under the radical is non-negative.
I see that you are not asked to find the range of the function above, which is uninteresting – it is the set of all non-negative numbers. There is no need to find the minimum of the quadratic function, as that minimum does not occur within the domain of f. If this isn’t clear, we can certainly discuss any questions you have about it.
If you have problems of the sort you described (finding the range of a function with a restricted domain), feel free to show us such a problem with your work, and we can discuss that. The process of finding the range can depend strongly on the details of the particular function. The parts of problem 8 that I can see, however, are all linear functions, so if that’s what you are asking about, it will be relatively easy. Pick one problem and give it a try, and I or Dr. Fenton can take it from there.
Another quadratic inequality
Mooija later showed work on problem 7e; I’ll insert that discussion here, and we’ll move on to 8 after this.
I am really sorry but I still don’t get how to solve the domain of a function.
In the attachment I tried two different methods; the first was wrong.
In the second method I think a) is right but the book says that b) is right, which means I am completely wrong, so please tell me what I’m doing wrong.
The error here is the same as before. Doctor Fenton answered with a different perspective:
You divided the inequality x(x – 4) ≥ 0 by x in the left half of the second line, getting x ≥ 0 on the left side of the third line, and then divided x(x – 4) ≥ 0 by (x – 4) on the right half of the second line, getting x ≥ 0 on the right side of the third line.
This method of simplifying the inequality doesn’t work in the same way it does for equations. The problem is that if you divide an inequality by a negative number, the resulting inequality is not true. For example, 4 < 6 is a true inequality, and if we divide the inequality by a positive number, 2, the resulting inequality is 2 < 3, which is also true. But if we divide 4 < 6 by a negative number -2, the resulting inequality is -2 < -3, which is false. When you divide x(x – 4) ≥ 0 by x, the resulting inequality x – 4 ≥ 0 is only true if x > 0.
While this process can be made to work by considering cases where x > 0 and where x < 0, it becomes messy. A simpler approach is to look at each factor in the problem separately, and find the values of x that make each inequality true: in this case, you find where x ≥ 0 and where x – 4 ≥ 0. The first inequality is already solved: x ≥ 0; and the second becomes x ≥ 4.
We can graph these solutions on the number line:
x ≥ 0 •-------------------------------------------------> x-4 ≥ 0 •-----------------------------> +----+----+----+----+----+----+----+----+----+----+----+----+----+ ... -2 -1 0 1 2 3 4 5 6 7 8 ...The top line shows the solution of x ≥ 0, in the sense that all points on the number line below the top line are solutions of x ≥ 0. Similarly, all the points under the bottom line are solutions of x ≥ 4 (or x – 4 ≥ 0). The product x(x – 4) ≥ 0 will be true if both factors have the same sign: both are positive or both are negative (or if one factor is 0). The points on the number line where that is true are the point under both lines, or not under either line. The points under both lines are the points where x ≥ 4 (we include 4 because the factor x – 4 = 0 there. The points not under either line are the points where x < 0, and we include x = 0 because we are only requiring that x(x – 4) = 0, which is true at x = 0. (If the inequality were x(x – 4) > 0, then we would not include either x = 0 or x = 4.)
Does this make sense to you?
Now we can move on to the range question.
Range with a restricted domain (linear)
Mooija had this to say about problem 8 and range:
To tell you the truth I am stuck with number 8, because I don’t know how to find the range with a domain of all real values.
If the domain is all real values it means the domain is basically infinite and so is the range.
Mooija has misstated problem 8, which specified the domain as “all positive real numbers”. This was to cause some misunderstandings.
Doctor Rick looked at problem 8(a):
You want to understand how to find the range of a function when the domain is restricted – when it is less than all real numbers. In problem 8, the domain is restricted to all positive real numbers; thus the answer you found does not help us – it’s talking about a different kind of problem.
Now let’s look at one of the parts of problem 8. If we define
f(x) = 2x + 7 with domain {all positive numbers}
then we’re asking, if x > 0, what inequality applies to 2x + 7? Watch as I start with x > 0 to get the result we want:
x > 0
2x > 2(0) (multiplied both sides by 2, which is positive)
2x > 0 (since 2(0) = 0)
2x + 7 > 0 + 7 (added 7 to both sides)
2x + 7 > 7
Thus I’ve found that 2x + 7, that is, f(x), must be greater than 7. That’s the range of f. All I did was to “build up” the function f(x) = 2x + 7 step by step, starting with x, and work with the inequality as I went to obtain an inequality equivalent to x > 0.
There are other ways one might approach the problem of finding the domain of a restricted linear function. We might think graphically, for instance — that may give you a better feel for what is going on. But this is a starting point for discussion, at least.
The “building up” approach works nicely here, but we’ll see the trouble Mooija gets into trying to use it naively in a quadratic case below.
Range with a restricted domain (quadratic)
Mooija showed us the rest of problem 8, which is about quadratic functions (and therefore takes us back to the original question about range):
There are other parts to number 8.
I have been able to solve them all except for one, the last one of number 8.
Doctor Fenton asked to see Mooija’s work, suspecting that the method might be wrong on all three even if the answers were right:
For problem 8(f), you say you had no trouble with the earlier parts of problem 8. However, the last three parts of problem 8 are very similar. Can you show me how you found the range in problem 8(d) or 8(e)?
Mooija answered, showing an incorrect attempt at the “building up” approach, which happened to work for (d) and (e), but was not robust enough for (f):
I did (d) and (e) but could not get (f) right, even though I used the same method I used in (e).
Doctor Fenton pursued this for a bit, having forgotten that the domain in problem 8 is restricted to positive numbers, so that merely finding the vertex is not enough. Doctor Rick rejoined with two ways to handle that:
Hi, Mooija, it’s Dr. Rick again. It’s probably getting confusing with all the back-and-forth, but I think another eye is needed. Let me take another look at problem 8(e).
You need to find the range of the function
f(x) = (x + 2)2 – 1; domain: x > 0
Here’s what I would do – similar to what I did with the linear function earlier. I start with the inequality defining the range, and change it step by step, doing valid things (things that produce equivalent inequalities):
[1] x > 0
[2] x + 2 > 0 + 2 = 2
[3] (x + 2)2 > 22 = 4
[4] (x + 2)2 – 1 > 4 – 1 = 3
Thus I’ve shown that f(x) > 3 for all x in the domain x > 0. That’s the answer the book gave.
We have to be careful when working with quadratics — the squaring step above, step [3], is only valid because we already know that the quantity being squared, (x + 2), is positive. If the domain were x < 0 instead of x > 0, the same set of steps (seeming to give the result f(x) < 3) would be wrong – the correct range would in fact be x > -1 (the range of the unrestricted quadratic).
The graph of the function may help you to see what’s going on, as I suggested with the linear functions. The red graph in the attached image is f(x) = (x + 2)2 – 1 subject to the domain restriction x > 0; you’ll see that the lowest value of y on that curve is y = 3. The dashed curve is the rest of the quadratic, whose minimum y value is y = -1.
Similar, but different
Now Mooija tried 8(f):
Okay I did 8(f) using both your methods:
With Dr. Rick’s method I think I did something wrong.
With Dr. Fenton I missed a few steps.
The thing is even if those mistakes are corrected it will still be wrong because f uses the inequality ≥ where the rest does not, can you tell me why?
Doctor Fenton’s method referred to here did not take the restricted domain into account, and just used the vertex. He explained:
Your error in Dr. Rick’s method is where you squared (x – 1) > -1 to get (x – 1)2 > 1. If a < b, then you can only conclude that a2 < b2 if both a and b are positive. For example, -1 < 0, but it is not true that (-1)2 < 02 : that would say that 1 < 0.
You conclude that (x – 1)2 > 1 for all x > 0, but that is not true. If x = 1, then x – 1 = 0. so (x – 1)2 = 0 and (x – 1)2 +2 ≥ 2. (If you know what increasing functions are, then you are treating (x – 1)2 +2 as if it were increasing on the interval x > 0, but it actually decreases for 0 < x < 1, and then increases for x > 1.)
When you try to use “my” method, you go from x > 0 directly to (x – 1)2+2 > 2. That suggests that you think that because x > 0, that (x – 1)2 > 0, but when x = 1, (x – 1)2 = 0, so (x – 1)2 + 2 ≥ 2.
This goes back to what I said above, that if a < b, then we can only conclude that a2 < b2 if a and b are both positive. In problem 8(e), you wanted the range of (x + 2)2 – 1 for x > 0. If x > 0, then x + 2 > 2, so you can conclude that (x + 2)2 > 4, since both (x + 2) and 2 are positive. In problem 8(f), the quadratic is (x – 1)2, so when 0 < x < 1, (x – 1) < 0, and so (x – 1) > -1. But since it is not true that both x – 1 and -1 are positive, you cannot conclude that (x – 1)2 > (-1)2.
Then Doctor Rick added:
You will recall that after I showed my method for problem 8(e), I pointed out that it won’t always work — only when both quantities to be squared are known to be positive. As Dr. Fenton said, problem 8(f) is one of the problems for which that caveat applies. So you’ll need another method …
I don’t know what methods you are being taught for solving these problems. Personally I would sketch a graph of the parabola and make decisions based on that. If you have learned to sketch parabolas, then you know that the graph of the function
f(x) = (x – 1)2 + 2
is a parabola with vertex at a certain point, and that it opens upward. This tells us that, regardless of domain restrictions, the value of f(x) cannot be less than the y coordinate of the vertex. If the vertex is to the right of the y axis (and hence in the domain of the function), then f(x) can in fact have that minimum value. And in that case, since the entire right half of the parabola is in the domain, there is no upper limit to f(x).
If you don’t have the background to do the work I just outlined, I’d like to see some information on what you have learned, particularly how any similar problems were solved in your textbook or class.
Here is the graph of this function:
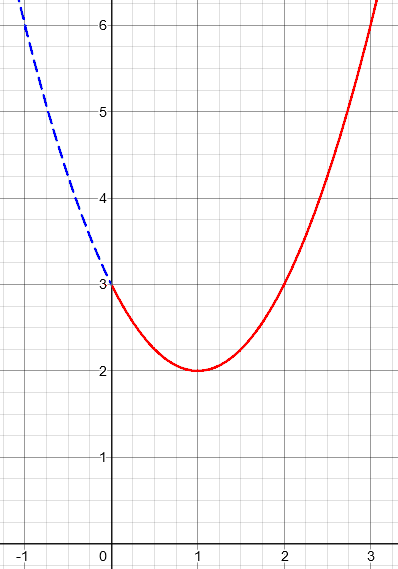
We can see that the minimum value is not at x = 0 as before, but at the vertex of the parabola.
These problems can be quite subtle. I would recommend at least checking your answer with a sketch of the graph, even if you carefully use a strictly algebraic method!

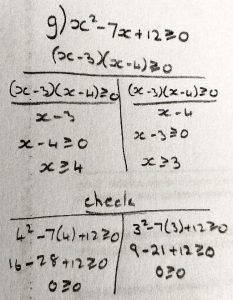

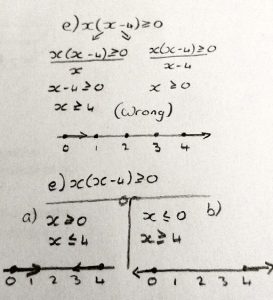
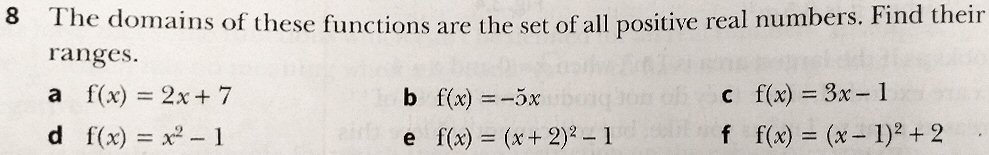

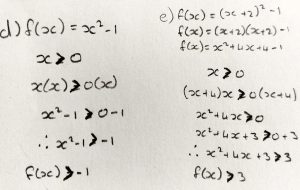
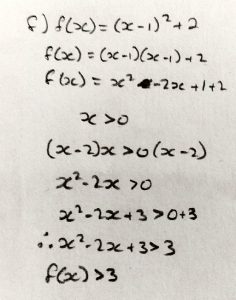
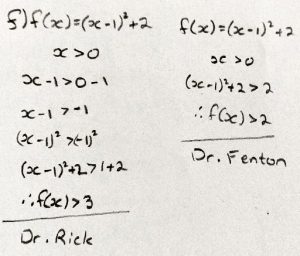
Pingback: Domain and Range of a Radical Function – The Math Doctors