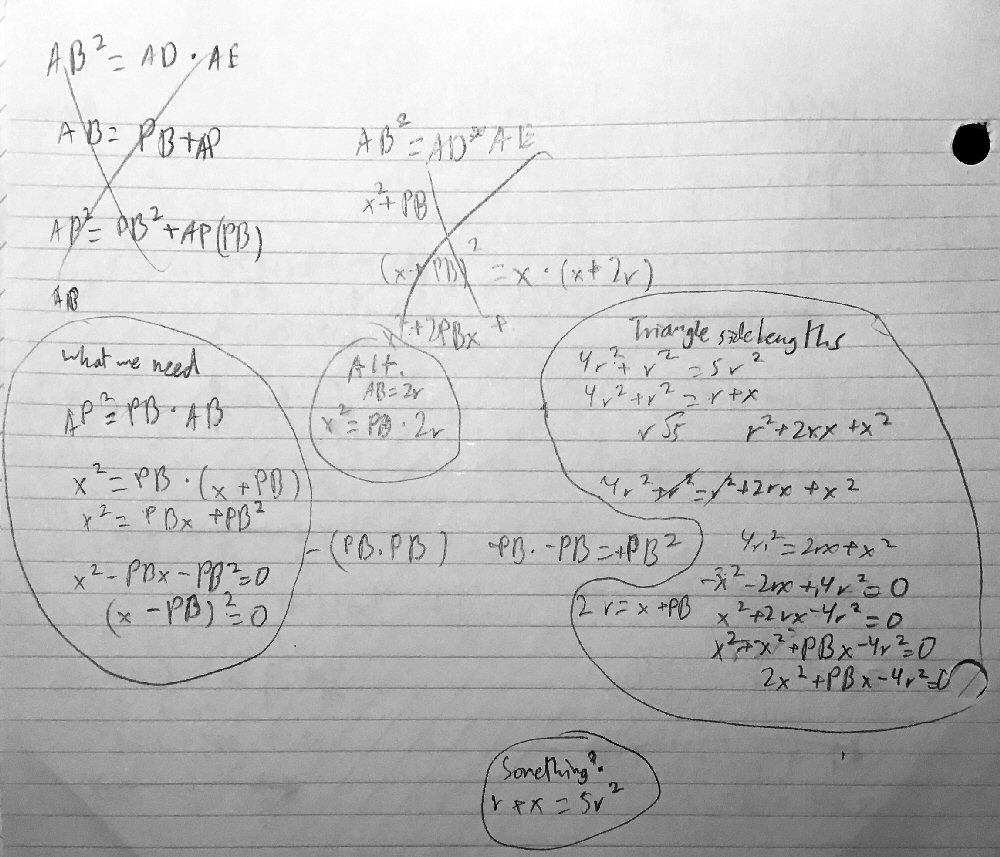One thing we enjoy doing is guiding a student through the process of problem-solving. Here is a problem from August that illustrates how to think through a complicated geometrical proof. In particular, this uses some circle theorems involving chords, secants, and tangents, together with a bit of algebra.
The problem
Here is the problem (I’ve replaced the original image of the problem with my own, which is cleaner):
Hi Doc!
I am having a difficult time trying to solve one problem with my homework, and I’d really appreciate some help with it.
The question goes as follows:
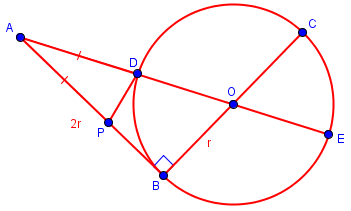
“Point O is the center of the circle, AB is perpendicular to BC, AP = AD, and AB has length twice the radius of the circle. Prove that AP^2 = PB*AB”
I’ve attached the graph as well:
This problem is from a geometry class I’m taking, and the teacher said this one was particularly difficult, and it definitely seems to be. We’ve learned the interior chord theorem, if that’s what it’s called, where if there were 2 chords, AB and CD that met up at P, AP*BP = CP*DP. Also, we’ve learned an exterior “chord” property? I’m not sure what to call it, but it’s when 2 chords AB and CD don’t intersect inside the circle but outside the circle by extending the chords outwards to meet at point P. If that is the case, then PA*PB = PC*PD. Also, if there is a line segment tangent to the circle PF, then PF^2 = PA*PB, or PF^2 = PC*PD.
We’ve learned a lot more than this, of course, but this is all the new things we’ve learned this week that is for the homework, and maybe a little bit of what we’ve learned before.
This is a very well-presented question! It illustrates well most of the recommendations I made in How to Ask a Good Question. When we pick up the question again below, we’ll see him show his work.
Background: Circle theorems
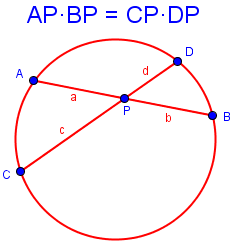
Before continuing with his question, let’s look at the theorems he has listed (which is an excellent thing to do, to give us context!). A good compact source I like to give students who don’t know these theorems is MathBitsNotebooks’s Rules for Chords, Secants, and Tangents in Circles. Eric’s “Interior Chord Theorem” is the Intersecting Chords Theorem:
Eric’s “Exterior Chord Property” is the Secant-Secant Theorem:
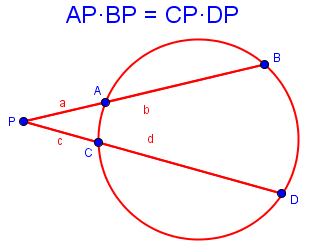
In both, the equation is \(ab = cd\), where b and d in the second theorem cover the entire segment shown.
Eric’s tangent property is the Tangent-Secant Theorem:
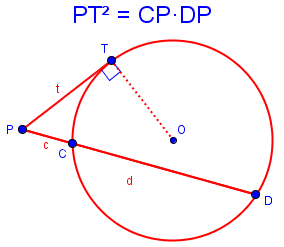
This is really the same fact, but a and b have joined to become a single segment t.
Together, these three theorems constitute Steiner’s Power-of-a-Point Theorem.
First attempt
Now Eric tells us what he has tried (again, an excellent example of how to ask us for help!):
I’ve been trying to figure out just what the problem wants me to find out since the question is asking something very obscure and unconventional, almost like it’s just coincidence that AP^2 = PB*AB. So, I decided variables are the way to go for this problem, and just use algebra to prove it.
I thought of maybe using x as a placeholder for AD and AP, but didn’t really do anything with it, or maybe using r for radius as a variable too. I do know that AB is 2r, so I tried substituting that into equation AB = AD*AE to get AD = -(AD^2/2r), and I’m not sure what to do with that strange value. I also attempted to make a triangle out of the graph, by connecting A and C, yielding AC = 2r sqrt(2), but I’m not sure how that would help. Aside from these few thoughts, I’ve also just drawn lines and relationships all over the graph, to try and see if one line or angle equality would solve it all, but to no avail.
Could you try and guide me in the right direction, please? I’m very confused …
Best Wishes,
Eric
The use of algebra is indeed appropriate, though the algebra is clearly wrong. The introduction of a right isosceles triangle in an interesting observation, though it probably won’t help:
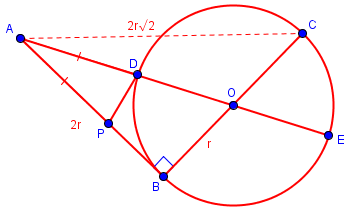
First corrections
I replied:
Hi, Eric.
I think you made a good start, and just tripped over a little mistake.
I myself took r as a constant, and let x = |AD|, as you suggested, then tried to solve for x, using triangle ABO.
On the other hand, what you started would lead to something equivalent, if you did it right. You said,
I tried substituting that into equation AB = AD*AE to get AD = -(AD^2/2r).
I presume you meant AB^2 = AD*AE; in any case, I don’t see how you got that result, which clearly makes no sense. I get a quadratic equation in x. Perhaps you should show me your work there.
But once you have the right equation, you may not need to actually solve for x. The first thing I had done was to write what we want to prove in terms of r and x. (General principle: write down what you are given, and what you want to prove, before you do anything else, so you’ll recognize the latter when you run across it.) In fact, I simplified that desired result a bit, in effect working backward from the goal. That helped a lot.
See what you discover!
(By the way, when a chord is extended to a line, that line is called a secant.)
Here I hinted at a place to start, using triangle ABO; I also encouraged Eric to continue with his method, and below I’ll be showing how both approaches work. I also gave some important general advice for solving complicated problems, including proofs. We’ll see it in action as we proceed.
I realize now, on looking at the image Eric had sent showing the problem (which I omitted above because it had been written on), that he had shown his work there: $$AB = AD\cdot AE\\2r=AD(AD+2r)\\2r=AD^2+2rAD$$ From there, he made some silly mistakes by misreading the equation; but since this started with an error, it wouldn’t have been right anyway. The correct equation would have been $$AB^2 = AD\cdot AE\\(2r)^2=AD(AD+2r)\\4r^2=AD^2+2rAD\\AD^2+2rAD-4r^2 = 0$$ which could be solved by the quadratic formula. (He also didn’t identify AD as x, as we are now doing.)
Second attempt
Eric responded:
Hey Doctor Peterson,
I tried doing what you said, by using the triangle to solve for x, and wrote what we needed to prove, but I’m not sure what to do next? I mean I think I tried to come across the answer… Did I just simply make a calculation mistake?
On the left, he has written the goal, \(AP^2=PB\cdot AB\), and expressed it in terms of the variable x, then expanded it, with the only mistake being in the last line. In the middle, he did that again, but using the given fact that \(AB = 2r\). On the right, he played with the right triangle ABO that I had mentioned, which leads to something useful, then went astray.
Second corrections
I answered:
Here are a few comments:
- In the lower left, you have (x – PB)^2 = 0. This is wrong; what do you get when you expand that?
- I would express PB as 2r – x; you want to express everything in terms of r and x.
- On the right you get x^2 + 2rx – 4r^2 = 0. This is correct. Stop there; you don’t want to go back to using PB.
- You got that using my right triangle ABO; you could also get it from the secant-tangent theorem you used before. (In your crossed-off work at top center, you did this but didn’t use the fact that x + PB = 2r.)
You’re getting close.
Here is the figure again, emphasizing triangle ABO and the variables:
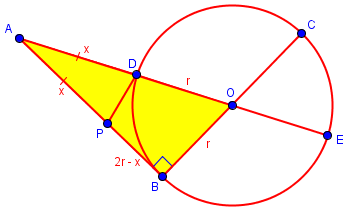
The Pythagorean Theorem applied to ABO yields $$r^2 + (2r)^2 = (x + r)^2\\r^2 + 4r^2 = x^2 + 2rx + r^2\\x^2 + 2rx – 4r^2 = 0$$ which he had on the right; equivalently, at the top he had used the tangent-secant theorem to write what could have become $$AB^2 = AD\cdot AE\\(2r)^2 = x(x + 2r)\\4r^2 = x^2 + 2rx\\x^2+2rx-4r^2 = 0$$
Meanwhile, on the left, he had found (without using the value for PB) that the goal is $$AP^2 = PB\cdot AB\\x^2 = PB(x +PB)\\x^2-PBx-PB^2 = 0$$ which, after substitution with \(2r-x\) yields $$x^2 – (2r-x)x – (2r-x)^2 = 0\\x^2-2rx+x^2-4r^2+4rx-x^2 = 0\\x^2+2rx-4r^2=0$$ We could have made the substitution from the start: $$AP^2 = PB\cdot AB\\x^2 = (2r-x)(2r)\\x^2 = 4r^2-2rx\\x^2+2rx-4r^2 = 0$$ Either way, we have shown that the given facts are equivalent to the goal. This is not yet in the form of a proper proof (working from the givens to the goal), but we have a complete connection.
Success!
He replied:
Oh! I didn’t realize (for some reason…) that PB could be written as 2r – x. After rewriting the equation I ended up with x^2 + 2rx – 4r^2, which lined up with one of the equations for the triangle side lengths! Thanks for helping me through proving this question!
I answered:
Yes, it was important in my own work to label AB as 2r very early, so the fact that AP + PB = 2r was visible. And it was also important to have studied the goal or target thoroughly so I’d notice it. The other main feature was to write both the givens and the goal in terms of the same variables, so they would look alike. Making details visible is key.
This is a good example of the technique of working from both ends toward the middle, which is discussed here:
Let’s write it up now as a proof, by rearranging what we did above, reversing the path to the conclusion:
Given: Point O is the center of the circle, AB is perpendicular to BC, AP = AD, and AB has length twice the radius of the circle.
To prove: \(AP^2=PB\cdot AB\)
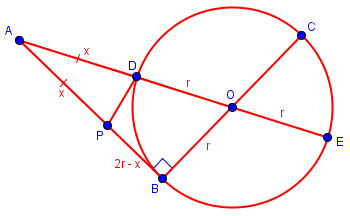
Let \(AP = AD = x\), and \(OB = OD = OE = r\).
We are told that \(AB = 2r\); and since \(AB = AP + PB\), \(PB = AB – AP = 2r – x\).
By the tangent-secant theorem, $$AB^2 = AD\cdot AE\\(2r)^2 = x(x + 2r)\\4r^2 = x^2 + 2rx\\x^2 = 4r^2 – 2rx\\x^2 = 2r(2r – x)\\AP^2 = AB\cdot PB$$
Q.E.D.
(Incidentally, this way of first working from both ends to the middle, and then turning your work “inside-out”, is also demonstrated, for trigonometric identities, in Different Ways to Prove a Trigonometric Identity.
There are probably several very different ways to prove this; let me know if you find one!