Last time we looked at how to use a ruler to measure distances. This time, we’ll consider another common question over the years: how to use a protractor to measure angles. We’ll also consider the relationship between protractors and the compass and straightedge constructions that started this series on geometry tools. And just like last time, I’ll add a bonus: why it has that name.
Drawing or measuring an angle
Although there were several short answers in the Ask Dr. Math archive already, our first extended discussion of reading a basic protractor was this, in 1998:
Using a Protractor I need to know how to find angles and to use a protractor. I made two parallel lines - now I have to intersect those lines making a 65-degree angle. Help!
Michelle had a specific task to perform, but her main need was to learn how to use the protractor; so I used the former as an example for the latter:
Hi, Michelle. Protractors can be a little confusing. Let's take out your protractor and look closely at it. Mine is not very round after passing through e-mail, but you should more or less recognize it:
90 /
_ - -+- - _ /
/ 9|0 \ /D
/ | / \
135 / | / \ 45
/ 45 | / 135 \
/ | / \
/ | / \
/ | / \
/ | / \
/ | / \
| | / |
| |/ |
-180+0-------------------+-----------------180+0---
A /C B
/
I was very new to Ask Dr. Math, and inserting pictures was not easy, so I did it the hard way. Here is a better picture (of a really cheap school protractor!):

What you should see on yours (and on mine if I could draw it better!) are: - a line along the bottom (AB), which you have to line up with the line you want to make a 65 degree angle with; - a cross or dot in the middle of that line (C), which marks the center of the angle you are going to measure (so you should first make a small mark there to show the point your line will go through); - a semicircle around the edge, with little degree marks; - degree labels around the outside, probably going in both directions (clockwise and counterclockwise) from 0 to 180.
Note that the vertex of the triangle does not go on the edge of the protractor (though that might be true for some that are not transparent like mine); the protractor has to be placed over the line you are using, with the vertex directly under the cross, and the line passing under the 0 mark.
Now let’s draw that 65° angle:

To draw a line at a 65-degree angle, facing to the right, look for the numbers that start at 0 on the right (that's the outside set of numbers on mine) and look along them until you come to 60 and 70. Just as on a ruler, there should be some number of divisions between them, and you should be able to identify a mark for 65 degrees halfway between 60 and 70. Make a small mark there (D), and then remove the protractor. Now you can use your ruler to draw a line between the marks (CD), and you're done!
On my protractor, we used the inside numbers. There are 10 marks between 60 and 70, and we chose the large one in the middle, for 5.
Though the question was only about drawing an angle, I added a comment on the opposite task:
If you have to measure an angle you've been given - maybe where the line you just drew meets the other parallel line - then you do the same thing in reverse. You line up the bottom edge with one of the lines that make the angle, with the center mark (C) over the place where the lines meet. Then you find which set of numbers starts at zero on the first line, and follow it until you come to the second line. Then you read the numbers just like a ruler. Have fun drawing and measuring, and let us know if you need more help, or if you discover any great theorems while you explore!
Measuring angles in a triangle
Three years later, someone named Chad asked another question that was added on to this page:
How do you use a protractor to find the three angle measures of a triangle?
Again, the goal is a specific task, but this time it’s not finding and drawing an angle, but measuring one that is already there, as in my extra comment above. There’s a little more to be said about that.
After referring to the answer above (the reason this one was added to the same page), I said,
I'll give you a few additional pointers for measuring a triangle.
First, if the triangle is smaller than your protractor, you will have to extend the edges, like this, so they are long enough to reach the edge of the protractor:
\ /
\ /
+
/ \
/ \
------+--------+------
/ \
/ \
This is not always needed, but it’s a good thing to check before you get started.
Now put the center of the protractor on one of the vertices, and line up the zero on one of the two curved scales with one of the edges coming from that vertex. Follow along that scale (watching the numbers increase from zero) until you come to the other edge (ray) of that angle. The number you find there is the measure of the angle.
My little triangle has a 65° angle:

You may have to count small marks to decide how many degrees each mark indicates. For instance, if the scale looks like
v
--+---+---+---+---+---+---+---+--
| |
70 80
then since there are five spaces between 70 and 80, each is 2 degrees (1/5 of 10 degrees), and the mark I am measuring is at about 77 degrees.
This example has marks every 2 degrees; 1-degree markings like mine are probably most common, but I wanted to show the harder case.
The 2° markings are common on better magnetic compasses (which, by the way, are more like protractors than like drawing compasses):

Cheaper compasses may have markings only every 5°.
Measuring acute, obtuse, and reflex angles
The next year, a student named Rezzi wanted information about various sizes of angles:
Measuring Angles with a Protractor I want to know how to measure acute, reflex and obtuse angles with a protractor.
Doctor Rick first reviewed the basics of protractor use that we have seen:
To measure an acute angle (less than 90 degrees), put the vertex at the center of the straight side of the protractor, lining up one half of that side with one side of the angle, so that the other side is under the protractor. On the curved edge of the protractor are (usually) two sets of numbers; one scale starts with zero on the left edge and increases to the right, while the other starts with zero on the right edge and increases to the left. Choose the scale that starts on the side that you lined up with a side of the angle. Read off the number from this scale at the point where the other side of the angle crosses the protractor.
This is the case we saw above. There’s really nothing different about an obtuse angle:
Measuring obtuse angles (between 90 and 180 degrees) works exactly the same way. It may be that some protractors have only one scale, with zero on both ends and 90 in the middle. If so, then you'll read a number between 0 and 90, and you'll need to subtract it from 180 to get the measure of the obtuse angle. For instance, if you read 45, the angle is really 180 - 45 = 135 degrees
I couldn’t find any examples of such a protractor online, so this is probably an imagined worst case. Normally, it will just look like this (where the 45 is there, but we didn’t have to use it):

Many readers will not be familiar with the term “reflex angle”; that measures from 180° to 360°:
A reflex angle is the "outside" of an acute or obtuse angle. Use the protractor to read the measure of the "inside" of the angle. Then subtract from 360 to get the measure of the reflex angle. If the inside is the same obtuse angle we just measured, then the measure of the outside is 360 - 135 = 225 degrees
Here is that 225° angle, in standard position, going counterclockwise from the right; we would have subtracted 225 from 360 in order to decide to make the mark at 135:
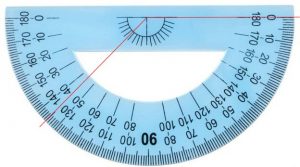
Some protractors are complete circles, so you could measure this angle directly.
Here are two other, shorter discussions of how to use a protractor, focusing on how to choose which scale to read:
Using a Protractor Reading a Protractor
What if it doesn’t start at 0?
In 2003 Gloria asked a specific question about measuring an angle, which was appended to the one above:
I have different pictures of a protractor with arrows pointing to different numbers on it. None of them starts at 0. This protractor is 0-180. If I have arrows pointing to 80-150, do I start at 0? Or would I just say 70 and subtract from 180? I'm confused!
I replied, guessing at the meaning of the problem:

I think you mean that you are supposed to find the angle between the 80 and 150 marks on the protractor. Although you would normally set the protractor so that one leg of the angle lies at zero, you can also use it this way. Remember that a protractor is really just a curved ruler, and can be used in exactly the same ways (apart from having to put the vertex of the angle in the right place). On a ruler, you can measure starting at zero:
0 1 2 3 4 5 6 7 8
+---+---+---+---+---+---+---+---+
=====================
5 inches
or between any two positions:
0 1 2 3 4 5 6 7 8
+---+---+---+---+---+---+---+---+
=====================
7-2=5 inches
You subtract the readings of the two ends to find the distance between them.
So the angle between the 80 and 150 marks is just 150-80 = 70 degrees. What you are really doing is subtracting two angles. If the points at the 0, 80, and 150 degree marks are P, Q, and R, and the center of the protractor is at O, then you are measuring angles QOR as POR - POQ. Draw a picture of that and see if it makes sense.
How can you make an accurate protractor?
Here is an entirely different question. In the past, we have talked about the fact that not every angle can be constructed exactly by compass and straightedge (in the post about trisecting angles); we recently looked more generally at the role of compass and straightedge in geometry. A reader named Ivan put these ideas together in an interesting question:
Precision in Measurement: Perfect Protractor? In the reply to a question regarding constructing an angle of one degree it was stated that an angle of one degree cannot be constructed using just a straight edge and a compass because the sine and cosine of one degree both require cube roots and only square roots can be constructed (http://mathforum.org/dr.math/problems/callanta.5.25.00.html). My understanding is that only construction using "perfectly" reliable instruments will give "perfectly" accurate results. If we have to resort to measuring and calculating then there has to be (as I see it) a certain amount of uncertainty regarding the result. Given that protractors are expected to be accurate to the degree and in some instances the minute or second how are such angles accurately constructed and marked? On the subject of precision, would you please tell me how to "60-sect" a one-degree angle so as to generate the markings for the minutes? Thanks for your help. Unfortunately I just don't have the maths to have even started on this. Once I got past bisection and trisection I referred to this resource and discovered that construction just can't be done (as I read it).
I focused on several different aspects of the question, starting with what compass and straightedge are primarily meant for: thinking about geometry, not making real things.
You are right that it is impossible to construct all the angles you need with compass and straightedge. But that isn't really necessary. First, there are other tools available to do constructions; the restriction to compass and straightedge is just part of the ancient Greek game of geometry, due to their desire to reduce all truth to the fewest possible starting points, or axioms. There are many ways to trisect an angle, starting with Archimedes' construction using a MARKED straightedge. See the Dr. Math FAQ: Impossible Constructions http://mathforum.org/dr.math/faq/faq.impossible.construct.html
That is, even mathematicians have considered other ways to do a theoretically exact construction of 1/3 of an angle, and the same could be done for other angles, in principle. But that’s just theory; practicality is different:
Second, a perfect construction is not necessary, or even useful, in making a protractor. The kind of perfection we talk about here is only a theoretical perfection: if we had a perfect straightedge, a pencil that actually draws LINES (with no width!), and so on, then we could prove that the result would be exact. But often such constructions, done with real tools, are actually LESS accurate than just measuring and estimating. That's because the construction can get very complicated and introduce errors repeatedly whenever we have to draw a line through a non-quite-perfectly defined "point."
Real pencil lines are never exact anyway!
One very reasonable way to mark a protractor would be to make a special tool with a 60:1 gear ratio, so that for every 60 degree turn of the handle, the marker would move one degree. Having marked degrees, if you are making a protractor large enough to show minutes, you could use the same tool to divide each degree into 60 parts. But usually we don't get that kind of precision. The marks on a typical protractor are not much less than a degree wide, so greater precision would be useless!
The protractor in my images is very imprecise, as you may have noticed (unless it’s just the image that’s distorted); this is probably true of many. But a very exact protractor can be made without much difficulty, given that the precision need be no better than the thickness of the lines drawn. If more precise angles are needed, my guess is that you would not use a protractor at all, but a machine much like what I described.
In summary: outside of a mathematician's mind, there are no "perfectly reliable instruments," nor is there a need for (or the possibility of) "perfectly accurate results." There is always uncertainty in the real world. So use whatever kind of measuring or calculating you wish. One reasonable way would be to use basic trigonometry to construct triangles with, say, 1- and 10-degree angles. (The larger one would allow you to construct the major divisions without having to build up large angles from many small ones, accumulating errors as you go.) You might construct 30- and 60-degree angles with a compass, since they are very simple and reliable, then fill in every 10 degrees, and then fill in the degrees between.
Ivan’s question was originally titled, “Marking my own protractor”, so he was asking about practical methods without fancy machines.
Why is it called a protractor?
We can close, as we did on rulers, with a question from 1999 about word origins:
Meaning of the Words Compass and Protractor Why is a compass called a compass when it protracts and retracts, and why is a protractor called a protractor when it is used to measure degrees? I know this is not really a high school math question, but it intrigues me a great deal.
“Protract” means “extend”, and a compass can be moved in and out, so one could call that protracting! And measuring angles doesn’t sound anything like “protraction”. What’s going on?
I replied:
Hi, Heather. This is not exactly a math question, but I like to talk about words too! The word "compass" means "to go around, encircle"; it originally meant "to measure" by pacing (passus). Since a compass "goes around," this makes some sense.
You can envision “encompassing” something as making a circle around it, “pacing off” a circuit. As far as I can tell, the magnetic compass we briefly looked at above is called that mostly because its scale “goes around”.
"Protract" originally meant "to drag out, lengthen." How is that related to what a protractor does? My dictionary gives one definition as "[surveying] To draw to scale by means of a scale and protractor." I suspect that because scale drawings or maps make heavy use of angles (remember the AAA similarity theorem: a scale drawing is similar to the original), the protractor was originally thought of as a tool for protracting in this sense.
The “tract” in “protract” is the same as in “tractor”, meant for pulling things like plows (or spacecraft, if you’re thinking of a “beam”). But the words “drag”, “draw”, and “draft” are also closely related; in drawing or drafting a map, you are dragging a pencil around. To “protract” a map meant to “draw it out”.
Words don't have to make sense to be used, but I think we can see at least a little sense in the history behind these words.

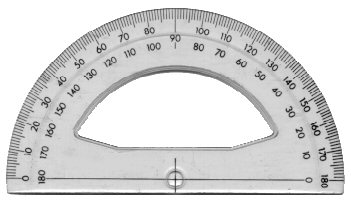
All I wanted to find out was if I read the outside of the protractor or the inside numbers.
Hi, Tansu.
The scales may vary from one protractor to another. As explained in the post, you need to find the 0 on your protractor (which is typically at one end of either scale), and just start reading from there, on that scale.
On both photographic images in the post, if your angle starts at the right side, the 0 is on the inner scale, so you would read where the other side of the angle crosses that inner scale, as in the 65 degree example.