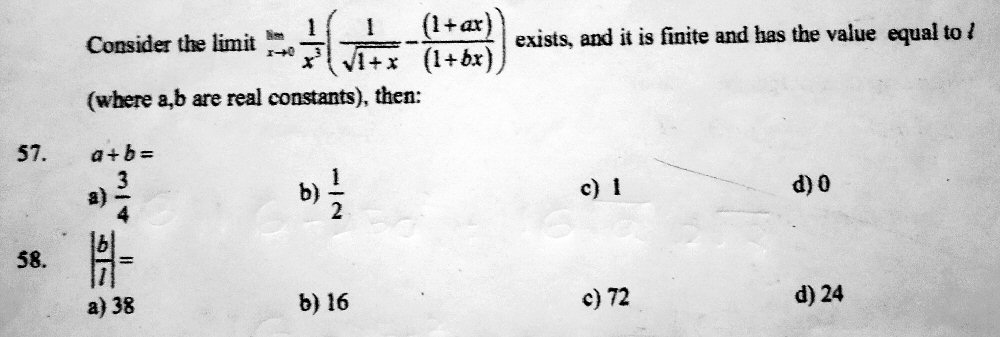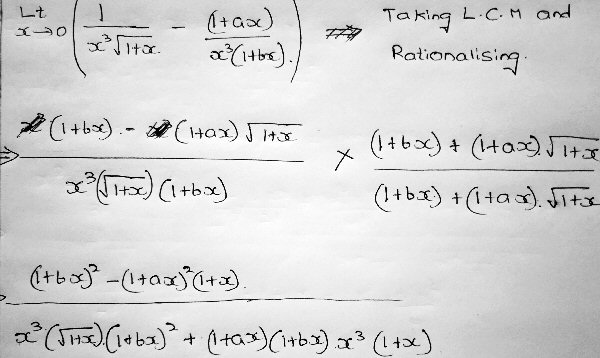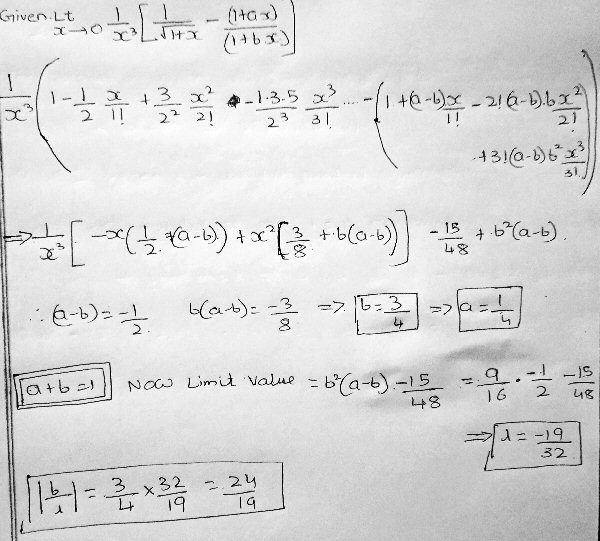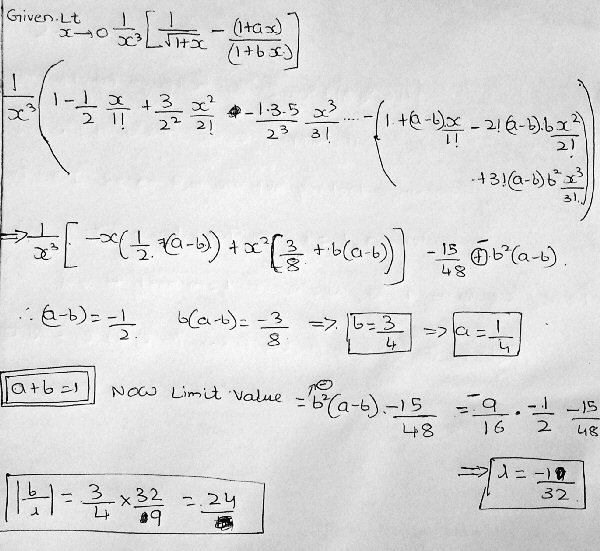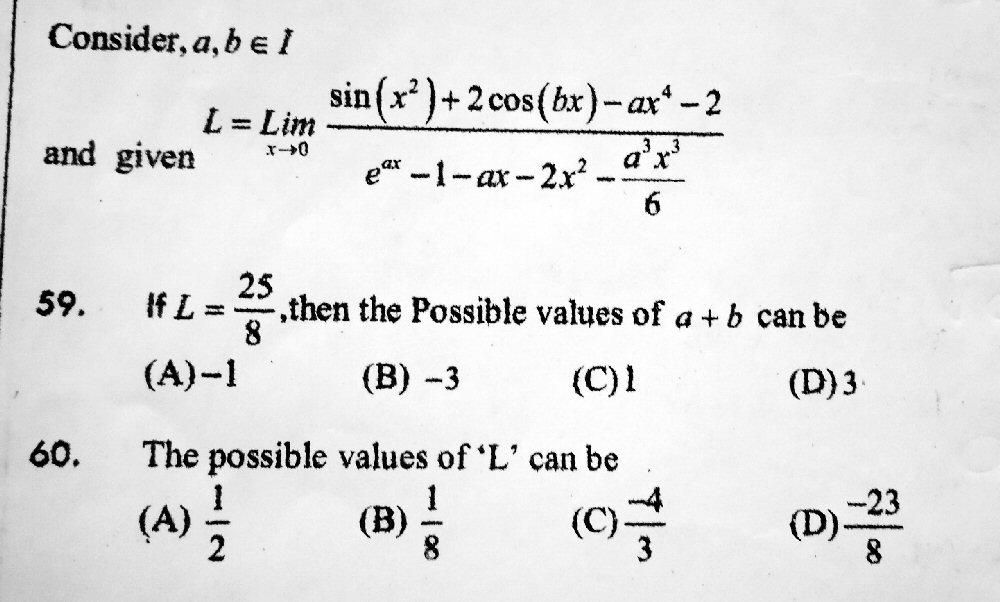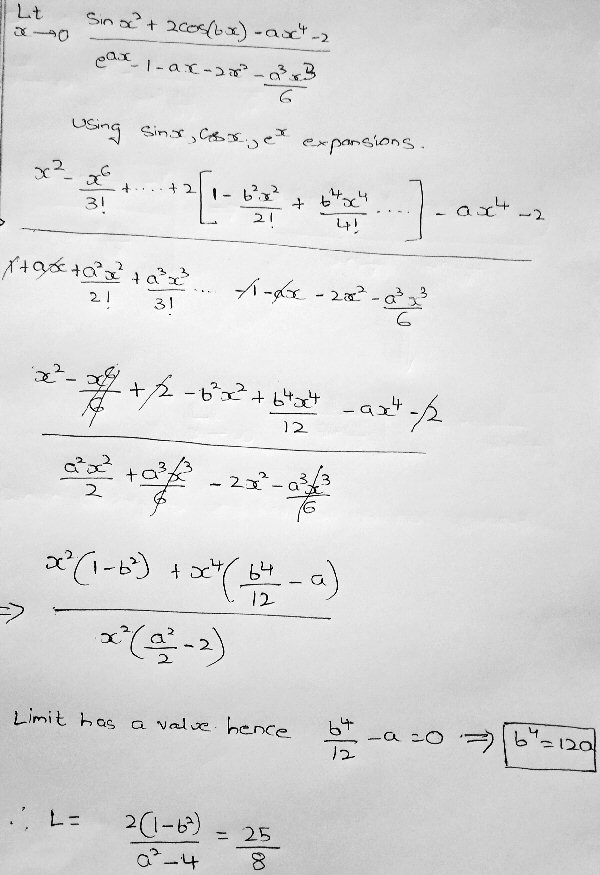(A new question of the week)
Limits can be challenging. They can be even more challenging when they require L’Hôpital’s rule or more advanced methods (Maclaurin series), and then are turned inside-out by asking not for the limit itself, but for parameters that will result in a specified limit, or what values of the limit are possible. Two of us helped with such problems in November.
First problem
Here is the easier of two questions Vignesh sent us 20 minutes apart:
Hello
I have tried to solve the problem but at its first step it has become a complicated equation. Help me to solve it if I am in correct way or else guide me the perfect way to solve it.
NOTE: Multicorrect question.
The simplification is indeed going in an unpleasant direction. (Or is it? Hold that thought.)
Don’t simplify first (for a change!)
Doctor Fenton answered, suggesting the use of Maclaurin series (the approach, as we’ll see, that Vignesh had already used in the other problem), without first combining the fractions:
Hi Vignesh,
I would recommend expanding the two terms in the parentheses into Maclaurin series and combining them into a single series for the difference, which then becomes the numerator of a fraction with denominator x3.
Then the only way that fraction can have a finite limit as x→0 is for the constant term and the coefficients of x and x2 in the series all to be 0. That will give you equations which determine a and b. With values for a and b, you can determine the limit.
Vignesh replied, clearly very familiar with the technique:
Hello Doctor Fenton
With your suggestion I expanded the two terms in the parentheses and got the value of ‘a’ and ‘b’ which made me to complete #57, also I have done #58 but no option matched with it. Once go through the sum, if I had done a mistake please tell me.
Examining the series expansion
Series expansions can be a powerful method for dealing with limits like this. Let’s look carefully at what he is doing.
The first fraction expands using the following Maclaurin series, for which Vignesh is using a formula, while I’ll use it as given in Wikipedia:
$$(1+x)^{-\frac{1}{2}}=1-\frac{1}{2}x+\frac{3}{8}x^2-\frac{5}{16}x^3+\cdots$$
This is a special case of the binomial series. The second fraction can be expanded using the following basic form, which can be found by mere long division (or by working backward from the geometric series):
$$\frac{1}{1-x}=1+x+x^2+x^3+\cdots$$
Applying this to \(\displaystyle\frac{1+ax}{1+bx}=1+(a-b)x\frac{1}{1+bx}\), by replacing \(x\) with \(-bx\), we get
$$1+(a-b)x\left[1+(-bx)+(-bx)^2+(-bx)^3+\cdots\right] =\\ 1+(a-b)x\left(1-bx+b^2x^2-b^3x^3+\cdots\right) =\\ 1+(a-b)x-(a-b)bx^2+(a-b)b^2x^3-(a-b)b^3x^4+\cdots$$
Subtracting those two series and combining like terms, we get $$\left[1-\frac{1}{2}x+\frac{3}{8}x^2-\frac{5}{16}x^3+\cdots\right]-\left[1+(a-b)x-(a-b)bx^2+(a-b)b^2x^3+\cdots\right] =\\ \left(-\frac{1}{2}-a+b\right)x+\left(\frac{3}{8}+(a-b)b\right)x^2+\left(-\frac{5}{16}-(a-b)b^2\right)x^3+\cdots$$
Dividing this by \(x^3\), we are left with $$\left(-\frac{1}{2}-a+b\right)x^{-2}+\left(\frac{3}{8}+b(a-b)\right)x^{-1}+\left(-\frac{5}{16}-(a-b)b^2\right)+\cdots$$
The omitted terms are all multiplied by positive powers of x, which will go to 0 so they can be ignored. The terms with negative powers of x go to infinity, so their coefficients must be 0; and the constant term will be the limit. This gives us two equations in a and b, $$-\frac{1}{2}-a+b=0\\\frac{3}{8}+b(a-b)=0$$ Solving the first for \(a=b-\frac{1}{2}\) and putting that into the second equation, we get $$\frac{3}{8}+b(-\frac{1}{2})=0$$ so that \(b=\frac{3}{4}\), from which \(a=\frac{1}{4}\). Vignesh is correct here, and therefore is right that \(a+b=1\).
The limit, then, is $$-\frac{5}{16}-(a-b)b^2=-\frac{5}{16}-(\frac{1}{4}-\frac{3}{4})\left(\frac{3}{4}\right)^2=-\frac{1}{32}$$
If you compare my work on the series with Vignesh’s, you will notice a sign error, which explains the wrong answer. (One sign error in all this work is impressive!)
Making it work
Doctor Fenton pointed out the one error:
I have a different sign for the b2(b-a) term in the coefficient of x3. That makes the limit -1/32 instead of -19/32.
Vignesh made the correction:
I made a mistake, instead of taking negative sign I took positive sign. Now I solved it, once check it.
Now the limit is \(-\frac{1}{32}\), and the requested ratio is 24, which is on the list.
Doctor Fenton:
That’s what I got. Good work!
P.S.
After I finished writing this post, I decided to check this answer by plugging in the values for a and b and finding the limit directly. I found that I could do so merely by using the complement … which is just what Vignesh had done in his initial work. Could we actually finish that work? Yes!
Here is the last line of his original attempt (with the denominator backed up one step to keep it a little simpler): $$\frac{(1+bx)^2-(1+ax)^2(1+x)}{x^3\sqrt{1+x}(1+bx)(1+bx+(1+ax)\sqrt{1+x})}$$
Expanding and simplifying the numerator, we get $$\frac{x(-a^2x^2+b^2x-a^2x-2ax+2b-2a-1)}{x^3\sqrt{1+x}(1+bx)(1+bx+(1+ax)\sqrt{1+x})}$$
The factors in the denominator apart from the first approach 2; so we need the numerator to cancel with the \(x^3\). We will have a limit, therefore, if \(-a^2x^2+b^2x-a^2x-2ax+2b-2a-1\) is a constant multiple of \(x^2\). That will be true only if the coefficients of the linear and constant terms are zero: that is, if $$b^2-a^2-2a=0\\2b-2a-1=0$$
What do you think is the solution to that? Yes, \(a=\frac{1}{4}\) and \(b=\frac{3}{4}\).
And what is the limit? $$\lim_{x\to 0}\frac{x(-a^2x^2)}{x^3\sqrt{1+x}(1+bx)(1+bx+(1+ax)\sqrt{1+x})}=\\\lim_{x\to 0}\frac{-a^2}{\sqrt{1+x}(1+bx)(1+bx+(1+ax)\sqrt{1+x})}=-\frac{1}{32}$$
So series were not really needed! But that method was enlightening, and leads us to the other problem …
Second problem
Vignesh actually sent the next problem 20 minutes before the other; it turns out to be considerably trickier:
Hello
I have started solving the problem and I think that I have done 90% solution but at last the equation had become quite complicated so that I am unable to finish it. Please help me.
NOTE: Multicorrect question.
Examining the series approach
Vignesh has used Maclaurin series (before Doctor Fenton had suggested it). Here are the basic series expansions he used this time:
$$\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots$$
$$\cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}+\cdots$$
$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots$$
In each case, something has to be substituted for x:
$$\sin(x^2)=(x^2)-\frac{(x^2)^3}{3!}+\frac{(x^2)^5}{5!}+\cdots=x^2-\frac{x^6}{3!}+\frac{x^{10}}{5!}+\cdots$$
$$\cos(bx)=1-\frac{(bx)^2}{2!}+\frac{(bx)^4}{4!}+\cdots=1-\frac{b^2x^2}{2!}+\frac{b^4x^4}{4!}+\cdots$$
$$e^{ax}=1+(ax)+\frac{(ax)^2}{2!}+\frac{(ax)^3}{3!}+\cdots=1+ax+\frac{a^2x^2}{2!}+\frac{a^3x^3}{3!}+\cdots$$
Only enough terms have to be written so that, after cancelling powers of x, remaining terms will go to zero. Using terms through \(x^4\) as Vignesh has done (but being a little more consistent), the numerator becomes $$\sin(x^2)+2\cos(bx)-ax^4-2=\\ \left[x^2+\cdots\right]+2\left[1-\frac{b^2x^2}{2!}+\frac{b^4x^4}{4!}+\cdots\right]-ax^4-2=\\x^2+2-b^2x^2+\frac{b^4x^4}{12}-ax^4-2+\cdots=\\ (1-b^2)x^2+\left(\frac{b^4}{12}-a\right)x^4+\cdots$$
and the denominator becomes $$e^{ax}-1-ax-2x^2-\frac{a^3x^3}{6} =\\ \left[1+ax+\frac{a^2x^2}{2!}+\frac{a^3x^3}{3!}+\frac{a^4x^4}{4!}+\cdots\right]-1-ax-2x^2-\frac{a^3x^3}{6} = \\ \frac{a^2x^2}{2}-2x^2+\frac{a^4x^4}{24}+\cdots = \\ x^2\left(\frac{a^2}{2}-2+\frac{a^4}{24}x^2\right)+\cdots$$
Canceling \(x^2\) leaves us with the fraction $$\frac{(1-b^2)+\left(\frac{b^4}{12}-a\right)x^2+\cdots}{\frac{a^2}{2}-2+\frac{a^4}{24}x^2+\cdots}$$
When x goes to zero, we are left with the limit $$\frac{(1-b^2)}{\frac{a^2}{2}-2}$$ You will observe a small difference in what I have done here. But at this point I hadn’t yet duplicated his work in that way; instead, I had taken a different approach in order to check his work independently. I’ll show that in a moment.
The L’Hôpital alternative
I answered this one, while Doctor Fenton was working on the other problem:
As I understand it, “I” means the set of integers (commonly called Z), so that a and b must be integers (positive or negative).
When you say the problem is “multicorrect”, I presume you mean that more than one answer can be correct, so you need to choose all choices in the list that are correct.
The word “the” in “the possible values” seems to imply that it is asking for all possible values of a + b, and likewise for #60? But if we take #60 this way, then it would be saying that #59 is impossible, as 25/8 would not be a possible limit. It must instead be asking merely which of the four values are possible limits.
I applied L’Hopital’s rule and obtained your equation (2(1-b^2)/(a^2-4) = 25/8. I didn’t find that b^4 = 12a.
Now we have a Diophantine equation which is equivalent to 25a^2 + 16b^2 = 116. This can be solved rather easily; but the solutions turn out to force you to take a further step.
L’Hôpital’s rule is closely related to the use of series expansions; it amounts to using only the first term or so. The limit we are to find is
$$\lim_{x\to 0}\frac{\sin(x^2)+2\cos(bx)-ax^4-2}{e^{ax}-1-ax-2x^2-\frac{a^3x^3}{6}}$$
This has the form 0/0, so we take derivatives of the numerator and the denominator, and get
$$\lim_{x\to 0}\frac{2x\cos(x^2)-2b\sin(bx)-4ax^3}{ae^{ax}-a-4x-\frac{a^3x^2}{2}}$$
This still has the form 0/0, so we differentiate again, and get
$$\lim_{x\to 0}\frac{2\cos(x^2)-4x^2\sin(x^2)-2b^2\cos(bx)-12ax^2}{a^2e^{ax}-4-a^3x}$$
Setting x to 0, this becomes $$\frac{2-0-2b^2-0}{a^2-4-0} = \frac{2(1-b^2)}{a^2-4}$$ which is what Vignesh got. So this has to equal \(\frac{25}{8}\). And we can cross-multiply the equation
$$\frac{2(1-b^2)}{a^2-4} = \frac{25}{8}$$
to get
$$2(1-b^2)\cdot 8=25\cdot (a^2-4)$$
which simplifies to $$16-16b^2=25a^2-100\\ 25a^2+16b^2=116$$
But what about Vignesh’s \(\frac{b^4}{12}-a = 0\)? That comes from his second term in the numerator, which he is thinking has to be zero in order to have a limit; that would be appropriate if that term had degree less than 2. But since, after canceling \(x^2\), that will still be multiplied by \(x^2\), it does not have to be zero. By using L’Hôpital’s rule instead of series expansion, I never even got to see that, so I wasn’t tempted to misread it! So in fact, we don’t have a separate constraint imposed by the existence of a limit.
Moving forward
Vignesh replied, carrying out my suggestion to solve the Diophantine equation (that is, find all integer solutions):
I solved #59 with obtained Diophantine equation once check it. What step I have to do to solve #60?
This is good. I think I myself just saw immediately that \(a^2=4, b^2=1\) would work, and no other positive solutions for the squares are possible. We now have four solutions, each of which yields one of the four options given for the sum \(a + b\), so all of them appear to be correct. But …
A deceptive solution
I pointed out that there was more to do:
I mentioned a further step you need to take; that starts with checking. What happens when you put your values for a and b into your equation (2(1-b^2)/(a^2-4) = 25/8 ?
I haven’t yet looked at #60, but will do so now.
Vignesh replied,
Yes, when I put values of a and b in the equation I am getting ‘0’. Does it mean the values of a and b are wrong?
Yes, we get \(\frac{0}{0} = \frac{25}{8}\), which doesn’t really work.
I answered,
That means it is still indeterminate, so we can’t be sure yet what the limit will be.
I think you need to apply L’Hopital yet again to see under what further conditions, if any, the limit will be correct. (I started that, but didn’t yet get to the conclusion.)
Or there may be a better way.
That was the end of the discussion, for some reason, and I didn’t get to go further at the time. Let’s see if we can finish the problem now.
Equivalent to applying L’Hôpital’s rule a third time as I suggested, Vignesh could just use more terms of the series expansion. Let’s do it both ways, starting with mine:
Beyond indeterminacy: continuing with L’Hôpital’s rule
Differentiating a third time yields
$$\lim_{x\to 0}\frac{-12x\sin(x^2)-8x^3\cos(x^2)+2b^3\sin(bx)-24ax}{a^3e^{ax}-a^3}$$
which again has the form 0/0. (Note that we are assuming a and b are solutions of the equation above, so that we could apply L’Hôpital again!) So we differentiate a fourth time:
$$\lim_{x\to 0}\frac{-12\sin(x^2)-48x^2\cos(x^2)+16x^4\sin(x^2)+2b^4\cos(bx)-24a}{a^4e^{ax}}$$
This time we don’t get zeros; the limit becomes \(\displaystyle\frac{2b^4-24a}{a^4}\). We want this to equal \(\frac{25}{8}\), so we try our four possibilities, \((2, 1), (2, -1), (-2, -1), (-2, -1)\). We find that \(\frac{2b^4-24a}{a^4} = \frac{-23}{8},\frac{-23}{8},\frac{25}{8},\frac{25}{8}\) respectively. So the solution is \(a=-2,b=\pm 1\), and the answer to the problem is that \(a+b=-1\text{ or }-3\). Only two of the four apparent possibilities are real.
Continuing with the series method
Using series, the fact that I had to apply L’Hôpital twice more suggests we need two more terms for each expansion (through \(x^4\)), which happens to be what I did above (where Vignesh had gone that far only in the numerator): $$\frac{(1-b^2)+\left(\frac{b^4}{12}-a\right)x^2+\cdots}{\frac{a^2}{2}-2+\frac{a^4}{24}x^2+\cdots}$$
Letting \(a=\pm2\) and \(b=\pm1\), this becomes (with signs corresponding to \(a=+2\) and \(a=-2\) respectively) $$\lim_{x\to 0}\frac{0+\left(\frac{1}{12}\mp 2\right)x^2+\cdots}{0+\frac{2}{3}x^2+\cdots} = \frac{\frac{1}{12}\mp 2}{\frac{2}{3}} = \frac{1}{8}\mp 3 = -\frac{23}{8}\text{ or }\frac{25}{8}$$
So we need to take the negative sign for a, and the solution as before is \(a=-2,b=\pm 1\).
Finding possible limits
How about problem 60, which asked which of the values \(\frac{1}{2}\), \(\frac{1}{8}\), \(-\frac{4}{3}\), and \(-\frac{23}{8}\) are possible? Well, we’ve seen that last one, haven’t we? That’s the limit when \(a = +2\). (We found that while we were trying to make the limit \(\frac{25}{8}\), but it was a valid limit – one of two possible when the limit was still indeterminate after the first part of our work.)
But we need to go back to the expression we found for the limit:
$$L = \frac{2(1-b^2)}{a^2-4}$$
What are the possible values of L when the parameters are integers? Fortunately, we don’t need to find all of them (and probably couldn’t); we just need to try determining values of a and b that will work for each choice we are given for L.
Let’s start with \(L=\frac{1}{2}\). In solving the Diophantine equation $$\frac{2(1-b^2)}{a^2-4} = \frac{1}{2}$$ we find that it simplifies to $$a^2+4b^2=8$$ The only solutions are those we have seen before, \((2, 1), (2, -1), (-2, -1), (-2, -1)\), none of which yield \(L=\frac{1}{2}\). So this choice is out. Similarly, \(L=\frac{1}{8}\) also fails.
But when we solve $$\frac{2(1-b^2)}{a^2-4} = -\frac{4}{3}$$ we get the equation $$2a^2-3b^2=5$$ which in addition to the familiar solution, is also true for \(a=\pm 4,b=\pm 3\), or \(a=\pm 16,b=\pm 13\). So this, too, is a possible limit.
The answer is that, of the four choices offered, \(L=-\frac{4}{3}\) or \(L=-\frac{23}{8}\).
I think this problem was one of the more interesting ones I’ve seen, and provides some useful experience comparing the series and L’Hôpital approaches to a limit.