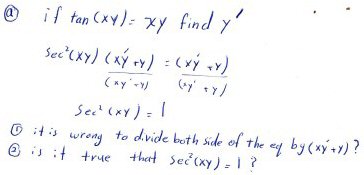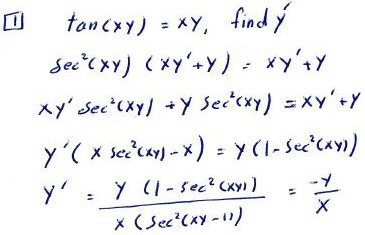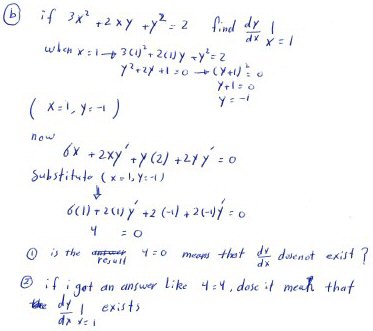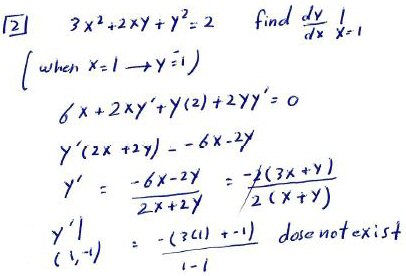(A new question of the week)
An interesting question we received in mid-January concerned two implicit derivative problems with an unusual feature: the derivative we are seeking disappears! How do you track down such elusive quarry? Each case is a little different.
Problem 1: The danger in division
Amia asked two questions, which I will separate to make the discussions easier to follow. Here is the first:
Hi Dr Math,
I have a question about finding the value of the derivative, I need your help.
Thank you.
This is an example of implicit differentiation, in which a relation (which we want to think of as \(y = f(x)\) though it is typically not a function) has been defined implicitly as representing any ordered pair \((x, y)\) that satisfies the equation \(\tan(xy)=xy\). He has differentiated both sides of the equation with respect to x, following the chain rule and the product rule, and obtained \(\sec^2(xy)(xy’+y)=xy’+y\), which he wants to solve for \(y’\), which will be a function of x and y. But something odd has happened: \(y’\) has disappeared entirely, so there is nothing to solve for! Was the division that led to this situation invalid? Is the resulting equation valid?
I answered,
In dividing by xy’ + y, you are assuming that xy’ + y is non-zero; and in the process you are losing the derivative completely! In effect, your answer seems to say that if the derivative can be determined at all, then sec2(xy) must equal 1. That’s the opposite of what a solution should say, which would be that if something is true, then the derivative has some particular value.
Instead, I would either distribute or factor the equation you got and isolate y’ as usual; when you do that, you will get an implicit derivative on the condition that sec2(xy) is not 1.
In general, when you are tempted to divide by a variable while solving, the better thing to do is to factor, which retains all relevant information rather than silently assuming something you may not want to assume.
After solving both problems, it will be interesting to try graphing the equations; I find that Desmos (almost) graphs both nicely, and the result is interesting to compare with what you find about the equations. But first try graphing by hand, at least to the extent of thinking about what kind of curve each must be. This will be worth discussing!
The warning against division is standard in algebra; an example I often use is that in solving $$x^2=4x$$ if we divided by x, we would get $$x = 4$$ and miss the solution \(x=0\); whereas if we rearrange and factor, we get $$x^2-4x=0\\x(x-4)=0\\x=0\text{ or }x=4$$ which is correct. The error was in implicitly assuming that the x we divide by is non-zero, when in fact zero is one of our solutions.
Similarly, in our problem, it will turn out that the \((xy’+y)\) that he divided by, when it is zero, leads to the answer we are looking for.
Getting the derivative
Amia first showed me the graphs, which I’ll hold for later, and then showed the work I’d described:
There’s a little slip in the last line; it should say $$y’=\frac{y(1-\sec^2(xy))}{x(\sec^2(xy)-1)}=-\frac{y}{x}$$
I answered,
This is good, though I would add that this is valid as long as sec2(xy) ≠ 1. This turns out to have no effect.
This is because the cancellation in that last line is valid only if \(\sec^2(xy)-1\) is not zero; if it is, then the intermediate form is just 0/0 and can’t be evaluated. In that case, we have to back up a line and observe that the equation is \(0=0\), which tells us nothing. And backing up still more, if we replace \(\sec^2(xy)\) in the second line of the work with 1, we already get a tautology (an equation that is always true). There is no way to determine \(y’\) in that case.
Now, why did I say that this restriction will not affect the final result? Because if \(\sec^2(xy)=1\), then \(xy=n\pi\) for some integer n; but then \(\tan(xy)=0\), and our curve is \(xy=0\), which is just the x– and y-axes. Hold that thought while we explore the graph.
Now, we’ve found that the derivative is \(y’=\frac{-y}{x}\).
Exploring the graph
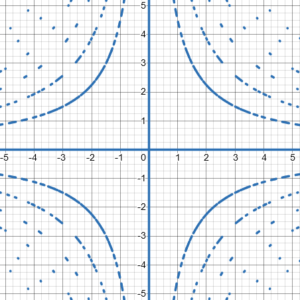
Do you know another function that has the same derivative (that is, that satisfies this differential equation)? It’s y = k/x, a family of hyperbolas — which is just what the graph you showed looks like (for some specific values of k):
(Desmos does a remarkable job graphing such a tricky equation, but it struggles, and you have to imagine those dotted lines being filled in to make complete curves.)
This kind of hyperbola, called rectangular hyperbolas because of the right angle between the asymptotes (the axes), has the equation \(xy=k\), and differentiating that implicitly we get \(y+xy’=0\), so that \(y’=-\frac{y}{x}\), the same as our curve. All we need to know is, what values of k are valid?
I’d suggested that we would learn a lot by trying to work out the graph ourselves rather than just plugging the equation into a website and seeing what it looks like all at once. We’ve just taken the first step, by observing that it is some set of hyperbolas, based on the derivative. We can continue by finding k:
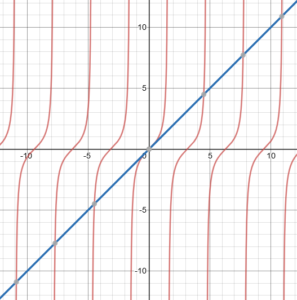
Now supposed we wanted to graph the function by hand. One way to analyze it would be to let u = xy, so the equation is tan(u) = u. This has as its solution certain discrete values of u:
Here I plotted \(y=\tan(u)\) in red, and \(y=u\) in blue, so that the intersections (gray dots) are the solutions. We can’t solve this analytically and exactly, but the graph tells us that they are about \(u=0,\pm 4.493, \pm 7.725, \dots\).
And our function therefore is equivalent to xy = k for those values of k, which is exactly the family of hyperbolas we’ve seen. Here I have overlaid two particular hyperbolas, namely xy = 4.493 (red) and xy = -7.725 (green)
That is very satisfying.
Now, if you wish, you can think about when sec2(xy) = 1.
This, as we saw above, corresponds to the x– and y-axes (the case \(k=0\)), and no other points on this graph. At those points, the derivative is 0 (when \(y=0\), and our formula for the derivative is correct) or undefined (when \(x=0\), and our formula for the derivative is effectively correct, yielding “infinity”). So the answer to the problem is, in fact, $$y’=\frac{-y}{x}$$
Problem 2: Getting specific too soon
Here is the second question, which we actually discussed interleaved with the first:
We can tell from the form of the equation that this is a conic section, and could further analyze it. But our goal is to find the derivative at a specific point on the curve. (This time we can actually solve for y and find these points given only x, which we couldn’t do in the first problem.) It should be observed that we would normally expect to find two points (if any), since we solved a quadratic equation; so this is a special point, and that alone might suggest what to expect.
But Amia has correctly differentiated and plugged in the given point, but again found that \(y’\) disappeared from the equation. All we have left is a false equation, \(4=0\). Does that mean “no solution”?Would it mean something different if you got a true equation like \(4=4\)?
(By the way, I have to admit I initially misread that as “\(y=0\)”, which would have meant something interestingly different. But Amia is consistent in distinguishing y from 4. Clear writing is important in math, but because people write differently, they can misread your writing even when you do everything right …)
To this, I answered:
You have correctly found that when x=1, y=-1; then you implicitly differentiated and substituted values before solving for y’, finding that y’ is eliminated, similarly to the other problem. This time you found that an inconsistent equation results. We can’t conclude (yet) that y’ doesn’t exist; but it does suggest that x=1 will be a special case of some sort.
Again, I would isolate y’ before substituting, which will result in something that is interesting. See what you find.
Getting the derivative
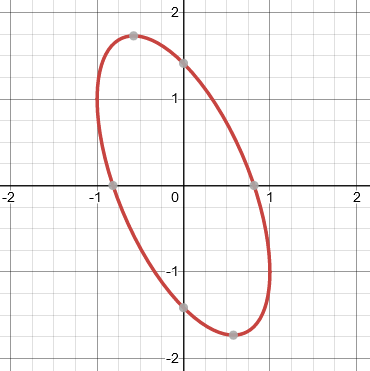
Amia showed the graph, showing the specialness of this point, and then showed the new work I had suggested:
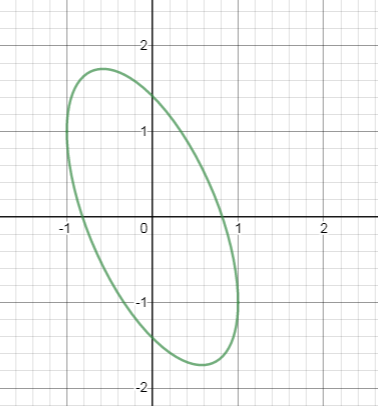
I see that the curve has a vertical tangent at the point (-1,1).
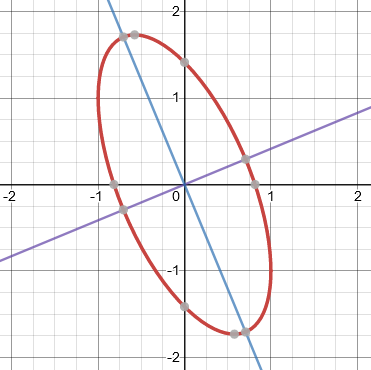
By solving for \(y’\) in the general case, we get a better sense of the behavior of the graph, and see how things fail at the special point. In general, $$y’=-\frac{3x+y}{x+y}$$ This is undefined when \(x+y=0\), which includes our special point \((1,-1)\) and its opposite, \((-1,1)\). But for other points nearby, the slope is defined, and we will be dividing by a very small number, making a steep slope, fitting our expectations for a vertical tangent. In particular, if x and y change just a little, we end up with something near -2 on top but a very small number, either positive or negative, on the bottom, resulting in a respectively negative or positive, near-infinite slope.
(But be careful – we can’t just think about the limit as we approach the point, because we have to approach along the curve, not just from any direction. Moreover, it turns out, though we can’t see it in the equations, that x can’t be greater than 1! There are many details about working with curves that we didn’t, and won’t here, touch on!)
Exploring the graph
I answered,
Again, this is good; in particular, we see that the requested derivative fails to exist in such a way that it indicates a vertical slope (approaching +infinity from one side and -infinity from the other). And that, again, agrees with the graph, as you indicated:
This is a rotated ellipse; here are its axes:
If in your initial work you had been given a different value of x (an interesting one is √(2)/2, which gives the vertices and covertices), then when you solved for y and plugged the values into the derivative, everything would have worked correctly. But this example shows that in general it is better to keep the variables unknown until the end.
These were both very interesting!
To talk more about the rotated ellipse, such as how I found the tilted axes, would take us too far afield. But if this made you curious, here is a thorough textbook explanation from Libretexts.
But let’s do what I suggested, and try taking \(x=\frac{\sqrt{2}}{2}\). First, we find y: $$3x^2+2xy+y^2=2\\ 3\left(\frac{\sqrt{2}}{2}\right)^2+2\left(\frac{\sqrt{2}}{2}\right)y+y^2=2\\ \frac{3}{2}+\sqrt{2}y+y^2=2\\ y^2+\sqrt{2}y-\frac{1}{2}=0\\ 2y^2+2\sqrt{2}y-1=0\\ y=\frac{-2\sqrt{2}\pm\sqrt{16}}{4}=\pm 1-\frac{\sqrt{2}}{2}$$ So the two points we get are \((0.707,-1.707)\) and \((0.707,0.293)\).
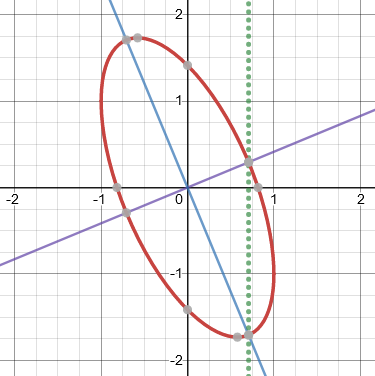
Now, using the formula we got for the derivative, we get $$y’=\frac{-(3x+y)}{x+y}\\ =\frac{-(3\frac{\sqrt{2}}{2}\pm 1-\frac{\sqrt{2}}{2})}{\frac{\sqrt{2}}{2}\pm 1-\frac{\sqrt{2}}{2}}\\ =\frac{-(\sqrt{2}\pm 1)}{\pm 1}=-\sqrt{2}-1,\sqrt{2}-1$$ These are the same as the slopes of the axes, \(y=\left(-1\pm\sqrt{2}\right)x\).