A recent question reminded me that we hadn’t yet covered the topic of radians yet. We’ll look at several questions comparing radians to degrees, concluding with the recent question: Is a radian a unit, or something else?
First, recall that a radian is defined as the angle for which the arc length in a unit circle is 1 (or, equivalently, for which the arc length in any circle is equal to the radius):
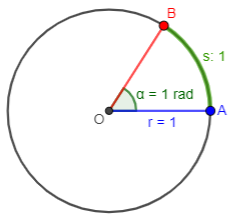
A degree can be thought of as the angle for which the arc length in any circle is 1/360 of the circumference; here is a 36° angle, whose arc is 1/10 of the circumference:
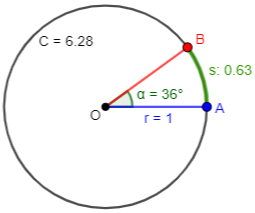
So the radian measure of any angle is the ratio of the arc length to the radius, while the degree measure is 360 times the ratio of the arc length to the circumference (which is what a common protractor measures).
Why did radians replace degrees? (Did they?)
We’ll start with this question from 2001:
Radians I have searched everywhere for the history behind radians. Why is it that they replaced degrees? Is there a history behind this? I thought it was because of the ability to have zero degrees in a circle, but I don't think this is the reason.
I answered:
Hi, Maddie. I wouldn't exactly say that radians replaced degrees - degrees are still very much in use. Each has its place: degrees work well for naming common angles with whole numbers (30, 45, 60, 90, rather than pi/6, etc.), while radians work well in calculus. You can find several explanations of the latter by searching our archives for the words radians degrees . Here's one: Why Radians? http://mathforum.org/dr.math/problems/munroe12.3.97.html
The basic reason for defining a circle as 360 degrees (which goes back to the Babylonians and the astronomer Ptolemy) is that the number has many factors, so most simple fractions of a circle are whole numbers of degrees: $$\frac{1}{2}\times 360^\circ=180^\circ\\\frac{1}{3}\times 360^\circ=120^\circ\\\frac{1}{4}\times 360^\circ=90^\circ\\\frac{1}{5}\times 360^\circ=72^\circ\\\frac{1}{6}\times 360^\circ=60^\circ\\\frac{1}{8}\times 360^\circ=45^\circ\\\frac{1}{9}\times 360^\circ=40^\circ\\\frac{1}{10}\times 360^\circ=36^\circ\\\frac{1}{12}\times 360^\circ=30^\circ$$ But there is nothing natural about this number; it’s just a matter of convenience.
You would expect that the metric system would use a unit like \(\frac{1}{100}\) of a circle, or \(\frac{1}{100}\) of a right angle (which is actually found on calculators, called a “grad”); but even in the metric system, the radian is standard.
We’ve discussed the origin of the degree and grad here:
Why is a Circle 360 Degrees? Degrees in a Circle Grad as a Measure of an Angle
But what about the radian?
The basic idea is that radians measure the arc length of an angle, which for small angles is close to the sine. That means that if you measure angles in radians, the slope of the graph of the sine is 1 at the origin. When you get to calculus, you find that the derivative of the sine is the cosine - it wouldn't be nearly as simple using degrees. And you can write infinite series and other formulas that give the value of the sine, which are much simpler using radians. Radians simply turn out to be the "obvious" unit to use for angles, once you've had plenty of experience with them.
We’ll see this illustrated below.
Using radians, we can just say \(s=r\theta\); that is, the arc length is the radius times the angle in radians. In degrees, it would have to be \(s=\frac{\pi}{180}r\theta\). Similarly, in radians, the derivative of \(\sin(x)\) is \(\cos(x)\), while in degrees it would be \(\frac{\pi}{180}\cos(x)\). For more on this, see
Radian vs. Degree, Sin Derivatives
Why can we treat radians as mere numbers?
Later in 2001, we got this deeper question:
Why Use Radians instead of Degrees? Hello everyone on the Math Forum team, For the past few days, I have been trying to figure out why we use radians instead of degrees. Some points that I have realised are as follows: 1. Radians have evolved from a circle. 2. A radian is a dimensionless quantity (this is probably the crux) 3. Radians provide simple formulae in terms of derivations of arc lengths and sector areas. But the problem still remains. For example, consider the Maclaurin's theorem. From the theorem we derive the Taylor series. Then suppose we have the series of sin(x), which goes as follows. sin(x) = x- (x^3)/3! + (x^5)/5! - ... Notice a strange thing here. To the right of this series are pure numbers, and suddenly to the left we get the answer in radians. Why is this happening? (Please send me the proof of Maclaurin's theorem, if possible).
How can a calculation (which we’ll look into more next time) that treats x as a mere number produce a trig function that treats x as an angle in radians?
Doctor Rick answered:
Hi, and welcome to Ask Dr. Math. All angle measures can be said to be dimensionless. A radian is the ratio of an arc length to a radius, and the ratio of two lengths is dimensionless. A degree is 180/pi radians, and the constant 180/pi is dimensionless, so a degree is also dimensionless. Trig functions are also by nature dimensionless. They can be defined as ratios of sides of a right triangle. Again, the ratio of two lengths is a dimensionless quantity (a "pure number").
An angle measure in radians represents, say, an arc length in centimeters divided by a radius in centimeters, so it is just a ratio. But a degree measure is just a multiple of that, so it is equally dimensionless. We just multiply the ratio by \(\frac{\pi}{180}\).
Thus there is nothing surprising about the dimensional analysis of the Taylor series for sin(x). The variable x represents a (dimensionless) angle, so the Taylor series represents a dimensionless quantity, as does the sine of x. You can see that dimensional analysis isn't much use in investigating what is special about radians as a measure of angles.
If we were adding, say, meters + square meters + cubic meters, it would make no sense. But adding pure numbers is reasonable.
And this is no different in degrees, so that is not what makes radians “better”. It’s just that the series is simpler for radians:
$$\sin(x)=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\dots$$
$$\sin\left(\frac{\pi}{6}\right)\approx\left(\frac{\pi}{6}\right)-\frac{1}{3!}\left(\frac{\pi}{6}\right)^3+\frac{1}{5!}\left(\frac{\pi}{6}\right)^5\\\approx\left(0.5236\right)-\frac{1}{6}\left(0.5236\right)^3+\frac{1}{120}\left(0.5236\right)^5\\\approx0.5236-0.0239+0.0000=0.4997$$
which is already close to its exact value, 0.5.
I consider the basis for the unique significance of radian measure to be this: The derivative of sin(x) is cos(x) (without any scale factor) when the angle is in radians. The MacLaurin series derives from this fact.
If we measure angles in degrees, then the derivative of the sine is \(\frac{\pi}{180}\) times the cosine.
Without going through the proof that the derivative of sin(x) is cos(x), we can see that the scale factor is 1 when the angle is measured in radians. Consider a unit circle and an angle near zero.
|
|
***********
***** | *****
*** | ***
** | **
** | **
* | *
* | * (x,y)
* | 1 ---+
* | ------- * s
* | ------ y|*
----*--------------------+-------------------+*----
* | x *
* | *
* | *
* | *
* | *
** | **
** | **
*** | ***
***** | *****
***********
|
|
The sine of the small angle is y/1 = y. The radian measure of the angle is s/1 = s. For small angles, y is approximately equal to s; therefore the sine of the angle is approximately equal to the angle.
sin(s) ≈ s
The slope (or derivative) of sin(s) with respect to theta is therefore close to 1 for small angles. If we know that the derivative of sin(s) is a*cos(s) for some scale factor a, then the sine of a small angle will be close to a*cos(0) = a. Therefore the scale factor must be 1 when the angle is measured in radians.
Here is the graph of the sine (in radians), showing that that slope is 1:
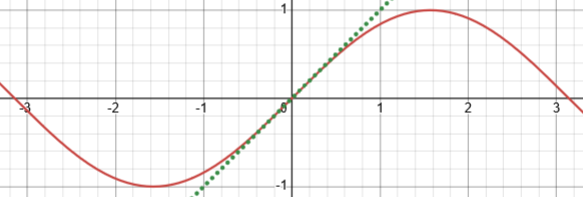
If you used a different angle measure, such as degrees, the angle would not be equal to s; it would be some constant (such as 180/pi) times s. The derivative of sin(x) would then be a constant times cos(x).
For comparison, here is the sine in degrees:
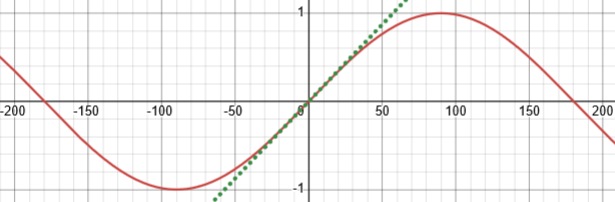
You can find discussions of the derivation of the MacLaurin series for sin(x) in our Dr. Math archives. Here is one such discussion: Power Series for Sine and Cosine http://mathforum.org/dr.math/problems/mark.10.12.00.html Does this satisfy your curiosity on this point? If you have more questions or thoughts, we'd be glad to talk about them. It's fun to discuss math with someone who is asking "why?"
We’ve said a lot more about these series, and will try to cover that topic soon.
Is it a unit, or not?
We’ll close with a question elaborating what was said in that answer about dimensions.
The recent question, from Debarghya, was
I know that radian = arc length/radius. So, it must be unitless quantity. But in some places I see that radian is mentioned as unit of measure of angle.
So is it a unit, or not?
I answered,
The radian is considered a unit, but it is “dimensionless“. As a unit, it specifies a scale; but having no dimension (being a ratio of distances), it is treated as a pure number in calculations, just as, say, the sine of an angle is.
Then I quoted the following, from 2003:
Are Angles Dimensionless? In the equation arc length = r*theta the numbers seem to work out fine, but the dimensions seem to be completely incorrect. In any circle there is a specific angle where the radius is equal to the arc length. This angle is defined as one radian and is approximately equal to 57.29 degrees. From this it can then be said that for every length of arc that is equal to the radius there is 1 radian of angle subtended. For any sector the angle will be so many lots of 1 radian, and thus the arc length will be the same number of times of the radius. From this you can then write: arc length / angle (in radians) = radius / 1 radian It can now be said that: arc length = angle (in radians) * radius / 1 radian This is not the same as the equation arc length = r * angle (in radians) Furthermore the r*theta equation seems to imply that the angle is dimensionless (has no units!). This is obviously incorrect, as it seems to imply that an angle can be measured with numbers. You have to have some way of measuring an angle just like you do with mass, or with length. Units are simply a standard measure of some parameter, which tell you what you are dealing with, whether it is length, mass, angle or whatever. The numbers just tell you how many of them you have. How you can say that the angle measured has no units goes against everything I know. But I am not arrogant enough to say the whole world is doing it wrong and I am doing it right. Can you explain to me what is going on here?
Another way to put this is that \(s=r\theta\) appears to say that \(meters=meters\cdot radians\), so either the units don’t match, or “radian” doesn’t really exist.
I answered:
Hi, Christopher. Angles are indeed dimensionless; the reason is that an angle is measured as the ratio of arc length to radius (meters per meter, say), which cancels out any units. Other angle measurements, such as degrees, are also dimensionless, though they are defined by different ratios, such as the ratio of the arc length to 1/360 of a circle, which results in the need for a multiplier. It is for this reason that we still need to name the unit, radians, rather than leaving it out entirely. Saying "radians" specifies the way in which the angle is measured; but it is still dimensionless and can be ignored as long as you know that radians are the correct method for the calculation being done.
So radians or degrees don’t function in a formula the same way units like meters do; they describe how a measure is being determined, functioning more as adjectives or adverbs that as nouns.
Since this is a tricky issue, I did a web search for references to support my opinion. Here are some: Why Use Radians instead of Degrees? http://mathforum.org/library/drmath/view/54181.html
This is the answer above, which I quoted from.
Next,
Glossary of Mathematics http://westview.tdsb.on.ca/Mathematics/R.html Radian Measure: A dimensionless unit of angle measure (as opposed to degree which has a dimension). An angle of one radian (1 rad) causes the ratio of the length of the arc of the circle's circumference to the radius of the circle to be one. Since this is a ratio the radian is not a unit and it is dimensionless. We have two different angle measures (pi radians = 180 degrees) since it is very troublesome to integrate or differentiate trig functions whose arguments are in degrees. One radian approximately equals 57.3 degrees. One of the real values of radians is that it is a non-unit "unit" (since it is the ratio of an arc length to the radius of a circle). That is, in any calculation using an angle measure, using radians does not introduce a new unit into the process to muddy the situation. If you are putting an angle into a trig function, it doesn't matter whether you use radians or degrees, since, for example, sin 30 deg. = sin pi/6 rad. = sin pi/6 (no unit). IF you are using an angle value in any other calculation, however, using degrees often produces non-sense. For example, evaluate the expression x^2-2x-4 for x being 30 deg. or pi/6 radians (or, therefore, just plain pi/6 with no unit). With degrees, the result is non-sense -- you get 900 square degrees - 60 degrees - 4. With radians, the non-unit "unit", the result is a pure, unitless number. Evaluating Taylor polynomials in order to get approx. values of the trig functions for any angle, then, requires radians to make any sense whatsoever. Calculators use similar methods to produce trig values, so if you ask your calculator for sin 30 degrees, it internally converts the angle to radians, uses that value in an algebraic expression that it has stored in a memory location that your "sin" key accesses, then produces the appropriate UNITLESS value for sin 30 degrees. Likewise in any other formula - in math, science, engineering, architecture, or whatever - if you have to use an angle in most any way other than in a trig function, radians are required and degrees produce non-sense.
Taylor polynomials, as mentioned above, are a way to calculate trig functions (or others), and only make sense for dimensionless numbers.
I added:
I disagree with this as to degrees; I would say the degree is still dimensionless, but is a different unit (scaling). But the radian is generally assumed, so that the degree requires conversion. For example, the Taylor series for the sine, as usually given, assumes that the sine function takes an angle in radians; but one could write a Taylor series for the sine of an angle in degrees, which would simply have different coefficients. There is no inherent difference, contrary to what this author says; it is just a rescaling. This is why we do include the radian as a unit in calculations, as a reminder of the correct scaling; but it can be ignored where necessary.
This is like other formulas where we don’t write the units, but require that the numbers we use are measured with the appropriate units.
Next, I quoted a NASA site that said, “The measure of the central angle of a circle is defined as the ratio of the subtended arc of the circle divided by the radius, that is, a ratio of two lengths. Thus, this measure is dimensionless but is assigned a special name of radians.”
Finally, I quoted the official U.S. standards for the metric system:
The Three Classes of SI Units and the SI Prefixes http://physics.nist.gov/Pubs/SP811/sec04.html The SI supplementary units are now interpreted as so-called dimensionless derived units (see Sec. 7.14) for which the CGPM allows the freedom of using or not using them in expressions for SI derived units. (Footnote 3) Thus the radian and steradian are not given in a separate table but have been included in Table 3a together with other derived units with special names and symbols (see Sec. 4.2.1). This interpretation of the supplementary units implies that plane angle and solid angle are considered derived quantities of dimension one (so-called dimensionless quantities - see Sec. 7.14), each of which has the unit one, symbol 1, as its coherent SI unit. However, in practice, when one expresses the values of derived quantities involving plane angle or solid angle, it often aids understanding if the special names (or symbols) "radian" (rad) or "steradian" (sr) are used in place of the number 1. For example, although values of the derived quantity angular velocity (plane angle divided by time) may be expressed in the unit s^-1, such values are usually expressed in the unit rad/s.
The current version, found here, says this in a footnote to a table:
(b) The radian and steradian are special names for the number one that may be used to convey information about the quantity concerned. In practice the symbols rad and sr are used where appropriate, but the symbol for the derived unit one is generally omitted in specifying the values of dimensionless quantities. (See Sec 7.10)
There, it says,
7.10 Values of quantities expressed simply as numbers: the unit one, symbol 1
Certain quantities, such as refractive index, relative permeability, and mass fraction, are defined as the ratio of two mutually comparable quantities and thus are of dimension one (see Sec. 7.14). The coherent SI unit for such a quantity is the ratio of two identical SI units and may be expressed by the number 1. However, the number 1 generally does not appear in the expression for the value of a quantity of dimension one. For example, the value of the refractive index of a given medium is expressed as n = 1.51 × 1 = 1.51.
On the other hand, certain quantities of dimension one have units with special names and symbols which can be used or not depending on the circumstances. Plane angle and solid angle, for which the SI units are the radian (rad) and steradian (sr), respectively, are examples of such quantities (see Sec. 4.2.1).
This is "official"! The radian is optional, and can be replaced by 1.
For further, current, support, see Wikipedia, which discusses various ways to make sense of all this.
Pingback: How to Evaluate Trig Functions (By Hand?) – The Math Doctors