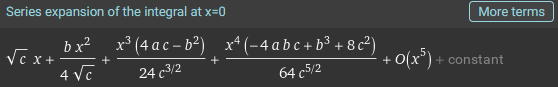Having looked at what it takes to work out an indefinite integral, using all our tools, we need to face something that isn’t explained often enough: Some integrals aren’t just difficult; they’re impossible! We’ll look at what we’ve said in several cases where this issue arose.
Why isn’t there an antiderivative?
First, consider this question from 2001:
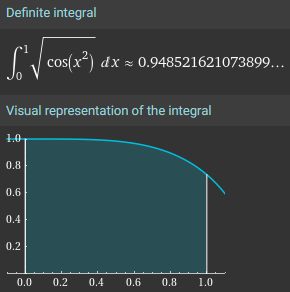
Derivatives and Antiderivatives When I run the formula int(sqrt(cos(x^2)),x=0..1) in Maple it just returns the formula. I know it's because there is no antiderivative, but why isn't there one?
Robert is trying to calculate a definite integral, $$\int_0^1\sqrt{\cos(x^2)}dx$$ using the mathematics software Maple. With the numeric option, that would produce a number, as Wolfram Alpha does today:
But his request didn’t work, because it was trying to produce a “closed-form expression”, not just a numeric value, and it couldn’t. For comparison, here is what WA gives when I ask it for the indefinite integral:
The question is, why doesn’t that work?
Doctor Rob answered:
Thanks for writing to Ask Dr. Math, Robert. There are many, many functions that behave similarly. For any of them, its antiderivative exists, but there is no expression for it in closed form in terms of familiar functions and constants. Examples are x^x, e^(x^2), e^(e^x)), e^(-x)/x, 1/ln(x), ln(1-x)/x, sin(x)/x, sin(x^2), sin(sin(x)), sqrt(sin(x)), e^sin(x), ln(sin(x)), sqrt(x^3+a*x^2+b*x+c), and so on.
Let’s see what Wolfram Alpha does for each of these; the differences are illuminating:
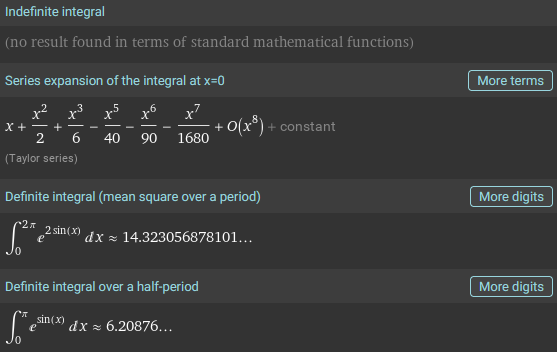
$$\int x^x dx$$
$$\int e^{x^2}dx$$
$$\int e^{e^x}dx$$
$$\int\frac{e^{-x}}{x}dx$$
$$\int\frac{1}{\ln(x)}dx$$
$$\int\frac{\ln(1-x)}{x}dx$$
$$\int\frac{\sin(x)}{x}dx$$
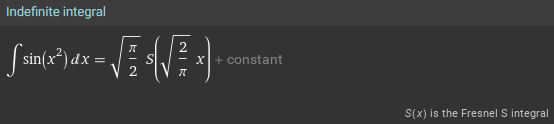
$$\int\sin(x^2)dx$$
$$\int\sin(\sin(x))dx$$
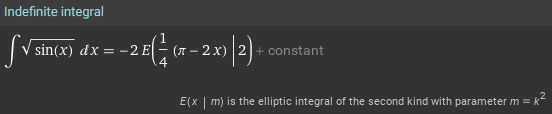
$$\int\sqrt{\sin(x)}dx$$
$$\int e^{\sin(x)}dx$$
$$\int\ln(\sin(x))dx$$
$$\int\sqrt{x^3+ax^2+bx+c}dx$$
Some of these, it just gives up on, and provides only an infinite series or approximation; others define a new function of their own; and others are expressed in terms of those new functions: \(\mathrm{erf}\), \(\mathrm{erfi}\), \(\mathrm{Ei}\), \(\mathrm{li}\), \(\mathrm{Li}_n\), \(\mathrm{Si}\), \(S\), \(\mathrm{H}_n\), \(E(x|m)\). We’ll be discussing these options as we proceed.
(Incidentally, when I am helping someone with an integral that looks difficult, I will sometimes give it to Wolfram Alpha just to see whether it’s worth trying; if the answer looks like any of these above, I ask the student to check whether they’ve copied the problem correctly!)
Now, back to the question:
The nonexistence of such an expression is a consequence of the fact that we only have a fairly small restricted set of functions to use to try to express antiderivatives: constant, rational, irrational algebraic, exponential, logarithmic, trigonometric, inverse trigonometric, hyperbolic, and inverse hyperbolic functions. This may seem like a big list to you, but it is not big enough for those purposes.
These basic functions arise from algebra or trigonometry; we can find the derivative of all of them in terms of others, but their antiderivatives open out into a bigger universe, so to speak.
One way to think of this is that the antiderivative is the solution of a certain differential equation: dy/dx = sqrt(cos(x^2)). You probably are aware that not all such solutions are expressible that way. Bessel functions and many other so-called "special" functions that crop up in engineering and physics arise as such solutions.
A course in differential equations necessarily includes a study of the use of infinite series, because many important equations can’t be solved any other way; the special functions are invented to provide an easier way to talk about the solutions.
Analogy: unsolvable algebraic equations
A similar situation exists with trying to solve the general quintic equation. The roots cannot be expressed in terms of the equation's coefficients using the above functions. The roots exist, and are continuous functions of the coefficients, but those functions just don't have simple expressions. Sorry!
Note the important distinction here: The solutions exist; we just can’t find a formula for them. We have a quadratic formula that gives the solutions of a general quadratic equation \(ax^2+bx+c=0\), and there are (much more elaborate) “formulas” for cubic and quartic equations; but there is no such formula to solve every quintic, \(ax^5+bx^4+cx^3+dx^2+ex+f=0\), even though every such equation has at least one real solution (and 5 complex solutions). The solution of some can be known exactly (such as \(2x^5-13x^4+6x^3+48x^2-56x+16=0\), whose solutions are \(-2,\frac{1}{2},2,3-\sqrt{5},3+\sqrt{5}\).
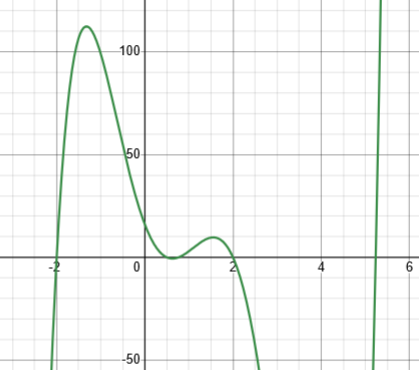
(I made up the equation starting with the solutions – otherwise there would be little chance of solving it.)
If I make a little change, say to \(2x^{5}-12x^{4}+6x^{3}+48x^{2}-56x+16=0\), we can no longer find exact solutions, but we can still see that they are there:
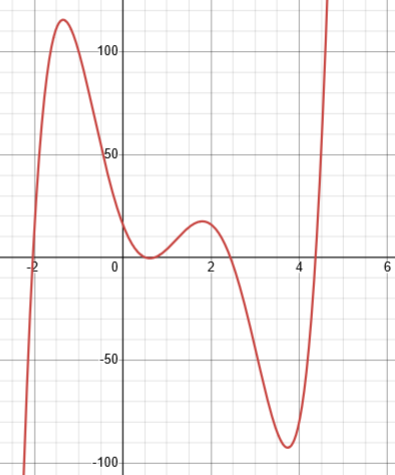
I often tell students that this is the dark secret of math teachers: We teach you only the problems for which we have methods; if you gave us a random problem, even in algebra, we probably couldn’t solve it. Math is a wild forest, but we give tours mostly of the cultivated orchards.
Anyway, the same is true of integrals: Many can’t be found exactly, and yet the function is still integrable: there is an antiderivative, but we just can’t write it out.
How can you tell whether it can be solved?
A 1996 question takes us deeper:
Integrating X^x, Closed Form (1) How would you go about integrating x^x? I don't have a clue where to start. (2) Also, how do you express the equation y = xcosx in terms of y? For both these problems, I have asked other people who have told me that there is no simple solution. If this is the case, please send the solution anyway, or at least give me some idea of the theory on which it is based.
Only the first question is directly related to our topic, but the second has an interesting indirect relationship. In both cases, it’s not so much that there is no simple way of solving it, but that there is no way to write the solution.
$$\int x^xdx$$
Doctor Jerry answered, going directly to the bigger question of how to tell whether there is a solution:
Dear Simon, (1) There is an algorithm due to a contemporary mathematician named Risch which can decide whether the anti-derivative of a continuous function f can be expressed as a finite combination of elementary functions. The elementary functions include polynomials, the trig functions, the inverse trig functions, the exponential function and its inverse, etc.
I know nothing about this algorithm, and with good reason: Wikipedia says,
Risch called it a decision procedure, because it is a method for deciding whether a function has an elementary function as an indefinite integral, and if it does, for determining that indefinite integral. However, the algorithm does not always succeed in identifying whether or not the antiderivative of a given function in fact can be expressed in terms of elementary functions.
The complete description of the Risch algorithm takes over 100 pages.
There are many functions - called special functions - which fail to have an anti-derivative expressible as a finite combination of elementary functions. The so-called elliptic functions, the error function, and the gamma function are a few examples. The error function, which is extremely useful in both physics and statistics, is defined as: erf(x) = (2/sqrt(pi))integral from 0 to x of e^(-t^2)dt Extensive tables of the error function would not exist if the anti-derivative of e^(-t^2) were expressible as a finite combination of elementary functions.
$$\mathrm{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^x e^{-t^2}dt$$
This is one of the special functions we saw above; we’ll look at it a little below. Then, there were tables of values for this (and other special functions) in which you could look up a numerical value; today, we let computers either use the same sorts of numerical method that were used to make the tables, or look them up in a table, or both. If you’ve ever looked up a probability for a “z-score” in a “standard normal distribution table”, that’s essentially what this is!
The anti-derivative of x^x is not expressible as a finite combination of elementary functions. I'm not sufficiently familiar with the Risch algorithm to even hint at a proof of it.
As I’ve hinted above, the only evidence I could point to (besides articles about this integral!) would be that Wolfram Alpha, or its relatives, give the sort of answer we saw.
Analogy: special functions we’re accustomed to
(2) As to solving the equation y = xcosx for x in terms of y, this can't be done in "closed form" or "by classical methods." Both of these phrases are used to mean that this equation can't be solved by algebraic methods or with pencil and paper methods. Of course, given a value of y, one can determine numerically (using Newton's method, for example) the values of x for which xcosx = y.
The goal here was to find the inverse of the function \(f(x)=x\cos(x)\), which is equivalent to solving the equation \(x\cos(x)=a\) for any given value of a.
Even more than the quintic equation, a “transcendental equation” like this can’t be solved exactly, even though solutions exist, as we can see, again, by graphing:
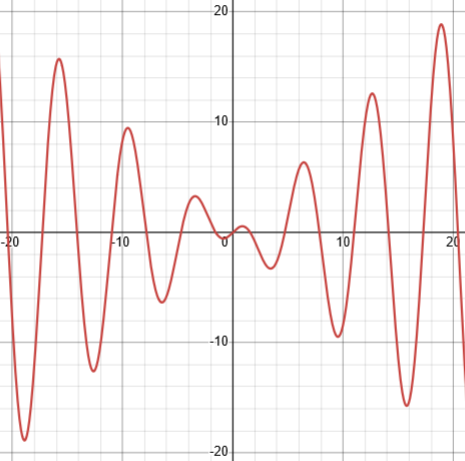
Notice that not only can’t we find an exact value of x for a given y, there are in fact infinitely many solutions, so this doesn’t have an inverse function.
But this raises an interesting question, even for a simpler problem of the same type:
I'd like to give a parallel question to y = xcos x. Can you solve the equation y = sinx for x in terms of y? If you say yes and write x = arcsin y, then you have only recognized that the function inverse to sine is a well known function and you know its name. You haven't actually found a finite expression for x. The fact is, neither sine nor arcsin are known in the sense that y = x^2 or x = sqrt(y) is known. Except for a few special cases, specific values of sine and arcsin must be looked up in a table or calculated numerically.
In other words, when we find a function that can’t be expressed in terms of known functions, we give it a name, and now it is a known function! This is the same thing we do when we need a function like erf or si. The arcsin function is just as special, and just as “made up”. We’re just more familiar with it, and don’t need calculus to understand what it does.
What do you do when you can’t integrate?
We’ll close with another question from 2001 that takes us to the next step:
Trying to Integrate f(x) = exp(-ax^2) How would you go about integrating a function of the form f(x) = exp(-ax^2)?
This is a very important integral, closely related to the erf function mentioned above: $$\int e^{-ax^2}dx$$
Doctor Jubal answered:
Hi Craig, Thanks for writing to Dr. Math. The function f(x) = exp(-ax^2) doesn't have an antiderivative that can be expressed in terms of other commonly used functions. What this means is you can't analytically integrate it.
As we’ll see, the antiderivative has a name, but that name doesn’t tell how to evaluate a definite integral, just as the name arcsin doesn’t provide a way to evaluate it.
Yet, the function pops up a lot in many places where it would be nice to be able to integrate it. So mathematicians have come up with several workarounds. Your options are: (i) Hope your limits of integration are zero and infinity. For these limits of integration, the integral does have an analytical solution. The integral of exp(-ax^2) from 0 to infinity is (1/2)sqrt(pi/a). If you'd like to see a proof of this, feel free to write back.
This one (improper) definite integral is important, because it’s used in normalizing the normal distribution:
$$\int_0^{\infty}e^{-ax^2}dx=\frac{1}{2}\sqrt{\frac{\pi}{a}}$$
We’ll be seeing that soon, because he did write back!
(ii) Solve it numerically. So your limits of integration aren't zero and infinity. Use Simpson's Rule or the numerical integration method of your choice to approximate the integral.
All sorts of software can approximate such an integral. For instance, we can use Wolfram Alpha:
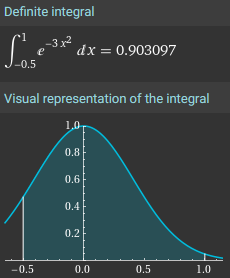
or we can use Desmos:
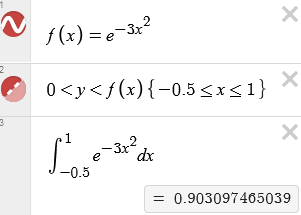
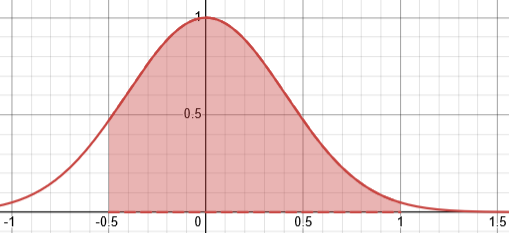
This presumably uses some numerical approximation method.
(iii) Use the error function.
Mathematicians like this integral a lot. They like it so much, in fact, that they defined a function just so this integral would have an "analytical" solution. The error function is defined
2 /x
erf(x) = --------- | exp[-t^2] dt
sqrt(pi) /0
and
/x sqrt(pi/a)
| exp[-at^2] dt = ---------- erf(x)
/0 2
The error function has been evaluated numerically at many, many points, and the results tabulated in mathematical handbooks. Essentially this is just doing (ii), but taking advantage of the fact that someone else has probably already done the work for you.
We don’t use tables much any more; but software knows how to handle it.
Finding the definite integral
Craig did respond by asking for the proof:
Hi, Could I see a proof of the integral of f(x) = exp(-ax^2) between 0 and infinity, please? Thanks.
Doctor Jubal replied:
Hi Craig, thanks for writing back. We want to evaluate /inf | exp(-ax^2) dx /0 However, using any of our usual arsenal of integration tricks to produce an antiderivative of this will fail. When I was an undergraduate, I spent five hours one evening attempting various ways to integrate this by parts and trying various substitutions. Little did I know there was no antiderivative. The solution came to me over breakfast, within half an hour of my waking up, thus illustrating that in mathematics, there is no substitute for a good night's sleep. But I digress.
His solution is a classic, probably one that has been reinvented many times!
Let's call the value of the definite integral value I.
For reasons that will become apparent shortly, it's a lot easier to evaluate I^2.
/inf /inf
I^2 = | exp(-ax^2) dx | exp(-ax^2) dx
/0 /0
$$I=\int_0^{\infty}e^{-ax^2}dx\\I^2=\left[\int_0^{\infty}e^{-ax^2}dx\right]^2\\=\left[\int_0^{\infty}e^{-ax^2}dx\right]\left[\int_0^{\infty}e^{-ax^2}dx\right]$$
It's rather irrelevant what symbols we use for the variables of integration, so I'm going to use x in the first integral and y in the second integral. This is okay because the two integrals are completely independent of each other.
/inf /inf
I^2 = | exp(-ax^2) dx | exp(-ay^2) dy
/0 /0
This is because the variable is just a placeholder: $$I^2=\left[\int_0^{\infty}e^{-ax^2}dx\right]\left[\int_0^{\infty}e^{-ay^2}dy\right]$$
And because the two integrals are independent of each other, we can combine them into a single double integral.
/inf /inf
I^2 = | | exp(-ax^2) exp(-ay^2) dx dy
/0 /0
/inf /inf
= | | exp[-a(x^2 + y^2)] dx dy
/0 /0
$$I^2=\int_0^{\infty}\int_0^{\infty}e^{-ax^2}e^{-ay^2}dxdy\\=\int_0^{\infty}\int_0^{\infty}e^{-a(x^2+y^2)}dxdy$$
We’re integrating one entire quadrant of this function:
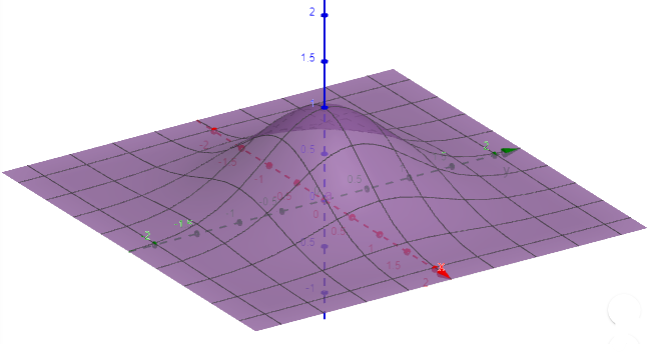
Now so far, it looks as if all we've managed to do is make a mess of things. This integral doesn't look any easier to deal with than what we started with, and we have an extra variable to boot. But we have managed to create an x^2 + y^2 term, which means this double integral may be more manageable in polar coordinates.
This is the key step. And we couldn’t do it for a finite integral, because a square region doesn’t fit polar coordinates.
The region of integration is the first quadrant, so we're integrating over r from 0 to infinity and theta from 0 to pi/2. I'll use Q for theta. Remember that in polar coordinates, r^2 = x^2 + y^2, and dx dy = r dr dQ.
/(pi/2) /inf
I^2 = | | exp(-ar^2) r dr dQ
/Q=0 /r=0
/(pi/2) /inf
= | dQ | exp(-ar^2) r dr
/Q=0 /r=0
This integral can be solved analytically, but I'll leave this as something for you to work out on your own. (Hint: try the substitution u^2 = ar^2).
He’s using Q as a stand-in for theta: $$I^2=\int_0^{\infty}\int_0^{\infty}e^{-a(x^2+y^2)}dxdy\\=\int_{\theta=0}^{\pi/2}\int_{r=0}^{\infty}e^{-ar^2}rdrd\theta\\=\int_{\theta=0}^{\pi/2}d\theta\cdot\int_{r=0}^{\infty}e^{-ar^2}rdr$$
This splits the double integral back into a product of two simple integrals.
Let’s finish:
The first integral is easy: $$\int_{0}^{\pi/2}d\theta=\left[\theta\right]_{0}^{\pi/2}=\frac{\pi}{2}$$
The second is a simple substitution: Let \(u=-ar^2\), so \(du=-2ardr\). Then $$\int e^{-ar^2}rdr=\frac{1}{-2a}\int e^{-ar^2}\cdot(-2ardr)=\frac{1}{-2a}\int e^udu=\frac{1}{-2a}e^u=\frac{1}{-2a}e^{-ar^2}$$
So the definite integral is $$\int_{0}^{\infty}e^{-ar^2}dr=\lim_{b\to\infty}\int_{0}^{b}e^{-ar^2}dr\\=\lim_{b\to\infty}\frac{1}{-2a}\left[e^{-ar^2}\right]_{0}^{b}=\lim_{b\to\infty}\frac{1}{-2a}\left[e^{-ab^2}-1\right]=\frac{1}{2a}$$
Putting it all together,
$$I^2=\int_{0}^{\pi/2}d\theta\cdot\int_{0}^{\infty}e^{-ar^2}dr\\=\frac{\pi}{2}\cdot\frac{1}{2a}=\frac{\pi}{4a}$$
$$I=\sqrt{\frac{\pi}{4a}}=\frac{1}{2}\sqrt{\frac{\pi}{a}}$$
as we were told.
Now, why is the error function, erf, defined with that strange constant multiplier? So that this will happen (taking \(a=1\)):
$$\lim_{x\to\infty}\mathrm{erf}(x)=\frac{2}{\sqrt{\pi}}\int_0^{\infty}e^{-t^2}dt=\frac{2}{\sqrt{\pi}}\cdot\frac{1}{2}\sqrt{\pi}=1$$