(A new question of the week)
An interesting geometry question came to us in July, about the area of overlap between two squares. The discussion was not long, but leads to some interesting ideas.
Here is the initial question, from Vignesh:
This is the problem I need help with:
Two square tiles of area 9 are placed with one directly on top of the other.
The top tile is then rotated about its center by an acute angle θ. If the area of the overlapping region is 8, compute 4(sin θ + cos θ).
Here is what I have done to solve it:
This is good work as far as it goes (and nicely written); unfortunately, we are left with one equation in two variables, x and θ, so we need another equation, or a different approach. One observation I make is that he hasn’t used the fact that the rotated triangle also has side length 3. That seems likely to be useful.
But one thing that immediately makes me curious is that they are asking, not for the value of θ, but the odd expression \(4(\sin\theta+\cos\theta)\). There must be something special about that quantity! This in turn makes me suspect that there is an “elegant” way to solve the problem, from which this expression will “fall out”.
Doctor Rick answered, not having a full solution to offer (which happens fairly often) but showing a start:
Hi, Vignesh.
I don’t have what I’d consider to be a satisfying solution to this problem yet. I have found the answer, but my expression for 4(sin θ + cos θ) is rather complicated – too complicated for it to be seen clearly even that the value is an integer, though my calculator suggests this strongly. There is probably some much more elegant method than mine.
I’ll start by providing you with an accurate figure that might give you more ideas. It will also give us a way to communicate clearly about, for example, specific triangles.
The main difference in this figure (apart from placing the letters a little differently) is the addition of names for the vertices of the rotated square, which may be needed in order to use what we know about it.
But also, being more accurate, it makes something clear that might not otherwise have been noticed: the white triangles are congruent to the blue triangles. This can easily be proved, or can be seen as “obvious” from the fact that each square is rotated relative to the other by the same angle, resulting in a useful symmetry. We’ll see whether these ideas are used; I’m just observing as an outsides!
The work you have shown so far is helpful; did you notice that it amounts to the fact that triangle LAE in my figure has area 1/4, so that the product of the legs of this right triangle is 1/2? We could call x = LA and y = AE, so that we have the equation
xy = 1/2
You have also written tan θ = y/x, which I used toward the end, after I had found the values of x and y. Again, though, what I did was rather ugly and you may find a much better way.
I was stuck with not much more than this, until I noticed that I could get another simple relation out of the area of triangle OEF.
Triangle LAE is 1/4 of the difference between the area of either square, and that of the overlap: \(9 – 8 = 1\).
Doctor Rick’s x is essentially the same as Vignesh’s, and his y is Vignesh’s \(x\tan(\theta)\). Doctor Rick has held off on using angle theta at all, preferring to find lengths without reference to the angle. If nothing else, this means avoiding trigonometry as long as possible, which might keep things simpler.
Let’s pretend we are Vignesh, and ponder the last hint: What can we see in triangle OEF? I’ve already mentioned something about EF, namely that it is the hypotenuse of a triangle that is congruent to LAE, so that we can express it in terms of x and y, namely \(z = \sqrt{x^2 + y^2}\). I also observe that if we drew lines from the center, O, to all eight vertices of the red overlap region, we would get 8 congruent triangles, so we know that ∠EOF = 45°. But the hint is about the triangle’s area … which is 1/8 of 8! Do you see how useful that will be?
About 40 minutes later, having continued working on the problem to be ready for a response, he wrote again:
I see it now! It becomes easy if we use (1) that observation I mentioned about the area of triangle OEF, (2) a fact I noticed earlier but didn’t mention, about the sum of the sides of triangle AEL in my figure, and (3) sin θ + cos θ expressed in terms of the sides of that triangle.
A couple more hints! What can we say about triangle AEL? This version of the figure may help:
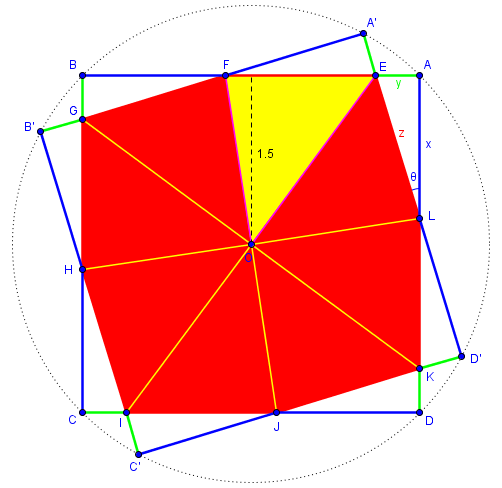
Here I’ve colored all segments of length x blue and those of length y green; those of length z are red. We can see that each side of a square consists of one of each; so \(x + y + z = 3\).
And how about \(\sin\theta+\cos\theta\)? Well, \(\displaystyle\cos\theta = \frac{x}{z}\), and \(\displaystyle\sin\theta = \frac{y}{z}\), so \(\displaystyle\sin\theta+\cos\theta = \frac{x+y}{z}\).
Vignesh wrote back,
Hello Doctor Rick.
I am unable to catch your point.
He replied with an encouragement:
My hints were not intended to make anything obvious! I still want you to do some hard thinking. It’s your problem and I don’t want to remove entirely the satisfaction of solving this challenging problem yourself. I’ll say a bit more, though.
Regarding triangle OEF, can you see what its area must be, given that the octagon EFGHIJKL has area 8, and considering the symmetry of that octagon? (In case it’s not clear, O is the center of the circle.) Also, if you take EF to be the base of the triangle, what expression gives the area in terms of EF?
Regarding the sum of the sides of the triangle, take a hard look at this:
AE + EF + FB = AB
Again consider symmetries that imply triangle congruences.
The hint about OEF was indeed that its area is 1. And since its height to O is half the side of the triangle, we see that \(\frac{1}{2}\cdot\frac{3}{2} z = 1\), so that \(z = \frac{4}{3}\). And since \(x+y+z=3\), we can conclude that \(x+y=3-\frac{4}{3}=\frac{5}{3}\).
Now we can answer the question: $$4(\sin\theta+\cos\theta) = 4\frac{x+y}{z} = 4\frac{\frac{5}{3}}{\frac{4}{3}} = 4\frac{5}{3}\frac{3}{4} = 5$$
I was right to surmise there was something special about this quantity. A very interesting problem, wasn’t it?


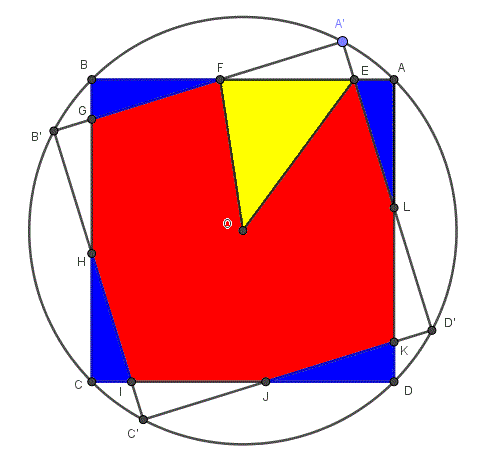
I do not understand how angle AEL is theta. In other words how angle AOA’ = angle AEL.
Thanks for pointing this out! I had accidentally marked theta as angle AEL instead of angle ALE, which is clearly what Doctor Rick intended, since he said that tan(theta) = y/x. I have fixed that.
With that correction, it should be clear: This is the angle through which any side of the square has been rotated. If it is not clear that this is equal to angle AOA’, there is a theorem about angles between chords by which it can be easily proved.
Thank you Sir,
I will check the theorem.
Regards.
I looked for the theorem but could not find any thing specific about the angles, but I could say the following,
AC and A’C’ pass through origin.
Chords CD and C’D’ are equal to 3. So angle CAD = angle C’A’D’. Let AC and A’D’ intersect at P, so angle A’PO = APD’ being opposite angles. So remaining angles, namely A’OA = theta and hence the angle A’LA is equal to theta.
Thanks.
Rahul.
That works. You have shown that triangles A’PO and APL are similar.
The theorem I had in mind is theorem #4 here. This says, in our case, that angle theta, between chords AD and A’D’, is equal to the average of the arcs AA’ and DD’, each of which is equal to angle AOA’.
Yes Sir, got it.
Regards,
Rahul.