(A new question of the week)
A good way to check (and hopefully build) a student’s depth of understanding is to assign non-routine problems, in which familiar ideas are twisted around so you have to come at them from a different direction. Here we’ll look at a question about a graph that can be solved either by algebra or by calculus, in either case by turning standard procedures inside-out. In working through the question, we will observe some useful ways to catch and correct errors.
The problem, and a faulty solution
The question came from Chase at the end of September:
I’m able to logically think through to the answer but don’t know if the logic is correct as I haven’t seen a problem worded like this before.
My work:
-x^2 + 4x – 8
m = 2x+4 = 8
x = -4/2(-1) = 2
y = -4+8-8 = -4
y + 4 = 8(x – 2) = y = 8x – 20
We were given y = x + k
so … k = -20
-23/4 = -5.75
therefore the answer is … k < -23/4
Is this all correct?
Chase differentiated the function and called the derivative m because it is the slope of a tangent line. (There is, however, a sign error.) Then he seems to have set that slope equal to 8 for some reason, and found the values of x and y where that slope occurs, namely (2, -4). (Because of the sign error, this actually turns out to be the vertex of the parabola, with slope 0.) Then he found the equation of the tangent there – all done correctly, apart from the sign error, but not answering the question. So the first thing to do is to clarify what is being asked.
Clarifying the problem
Doctor Fenton was the first to reply:
I don’t think you understand the question. You are given a parabola, and asked to find all the values of k for which the line with equation y = x + k intersects the parabola in two points. Lines with equations of the form y = x + k are all parallel lines with slope 1, and y-intercept k. When you have a parabola and a straight line, one of three things will happen. The line will not intersect the parabola; the line will intersect the parabola in one point (in which case the line is a tangent line to the parabola); or the line will intersect the parabola in two points.
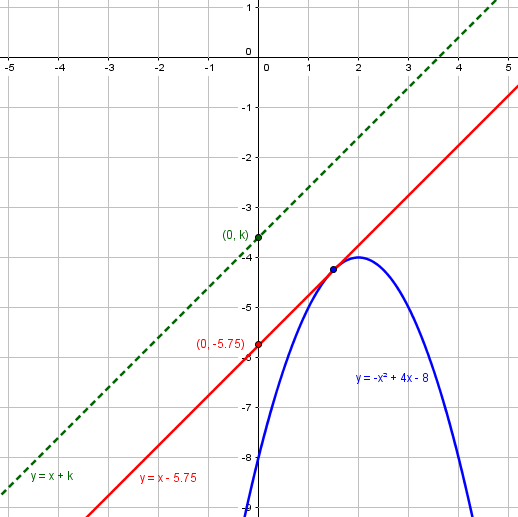
Here we see the parabola and three lines, intersecting it in, respectively, 0 (broken green), 1 (red), and 2 (purple) points:
We are to find values of k that will create “purple lines”.
Do you remember from algebra how you change the graph of a function y = f(x) when you add a constant to the right side, to get a new function g(x) = f(x) + k? If k > 0, the graph of g(x) is just the graph of f(x) shifted upward by k units, while if k < 0, the graph is shifted downward.
If you graph the parabola y = -x2 + 4x – 8, using a graphing calculator or going to WolframAlpha and entering
plot y = -x^2 + 4x – 8 ,
and look at some lines y = x + k for several values of k, such as y = x + 1 and y = x – 8, you will see two of those possibilities. The problem wants you to find all the values of k which cross the parabola at two points.
Do you remember how to find where two curves y = f(x) and y = g(x) intersect? If so, what does that tell you about this problem?
He has suggested making an image like mine to clarify the problem, and then suggested the beginning of an algebraic way to solve it. Let’s follow through on that right now, as we’ll soon be moving on to a different approach (Chase’s own).
An algebraic solution
We can find the intersection(s) of the line \(y=x+k\) and the parabola \(y = -x^2 + 4x – 8\) by setting the two expressions for y equal, and solving for x: $$x+k = -x^2 + 4x – 8\\x^2-3x+(k+8)=0$$ Here, I moved all terms to the left-hand side to avoid a negative leading term.
But we don’t specifically care about the actual solutions; we just want to make sure that there are exactly two of them – that is, we want to find a value of k for which this equation has exactly two (real) solutions. (If the solutions are not real, they won’t correspond to intersections on our graph.) How do we do that? By using the discriminant, \(D=b^2-4ac\) for the equation \(ax^2+bx+c=0\). If this is positive, there will be two real solutions; if zero, one; and if negative, none. So we calculate it, taking \(a=1,b=-3,c=k+8\): $$D=(-3)^2-4(1)(k+8) = -4k-23$$ We want this to be positive, so we solve the inequality $$-4k-23>0\\-23>4k\\4k<-23\\k<-\frac{23}{4}$$ And that is the solution we were given.
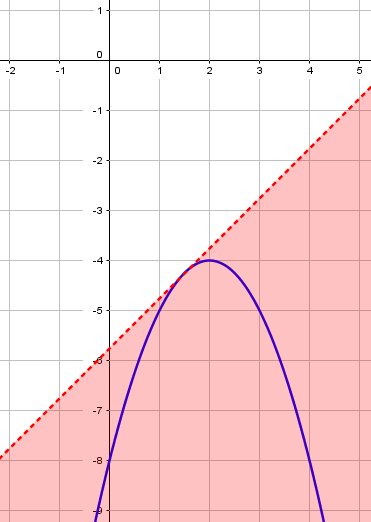
Here is a graph of the region formed by all lines \(y=x+k\) that intersect the parabola in two points:
Finding problems in the calculus approach
I had been looking at the question too, with a view to helping Chase improve his own work, rather than start over. So I joined in:
Hi, Chase. I’d like to offer a different perspective, by looking at your work to see what you were thinking.
Doctor Fenton suggested one way to solve this, using algebra; that is the first thing I did when I saw the problem, too. You are using calculus, which is also valid (and appropriate, given what you are studying). Unfortunately, you made a couple mistakes.
You apparently are looking for the point on the parabola where the slope matches that of the line, which can be a good idea. Unfortunately, when you differentiated -x^2 + 4x – 8, you missed the negative sign; the derivative should be –2x + 4, not 2x + 4.
Then for some reason you set this slope equal to 8; that would have been appropriate if the line were y = 8x + k rather than y = x + k. You should have set it to 1. (Were you perhaps basing your work on an example that used 8?)
Then you found the point (x, y) on the parabola with this slope, and the equation of the tangent line, all of which would have been correct apart from the two errors already mentioned. Good work on that part!
Then you presumably saw that, if your work was correct, the y-intercept of the tangent line would be the critical value for k, so that k would have to be on one side of that or the other. I would have used the direction in which the parabola opens to determine the appropriate direction, but there are other ways.
Apart from the unfortunate 8, whose source I can’t figure out, I saw good thinking; I like catching students doing something right. From here, unfortunately, the work seems to be a wild attempt to match the provided choices.
I imagine that at this point you saw that your -20 was not part of the choices, so you tried a wild guess and supposed that you were supposed to determine whether -23/4 was above or below your -20, which is wrong. You should have just gone back and checked your work. (This is just one of many reasons I dislike multiple-choice problems: they can lead you to try anything just to get one of the choices. “Reverse-engineering” a given answer to find a way to get it is rarely good for learning!)
So if you want to use the method you are following (perhaps because you were taught a similar method), go back and fix the parts I pointed out. You will find that -23/4 arises naturally as part of the work.
You might also want to try the algebraic method, which is useful in many other problems you may see later.
This illustrates why I emphasize checking work whenever I teach or tutor. This includes both checking the answer (here, perhaps by trying out a few values of k above and below -20), and checking the work itself (going through it line by line to find where it went wrong). It does not mean “checking” the back of the book or the list of choices, which are not available in real-world problems!
Redoing the work
Chase replied to me, setting aside the algebraic approach for the time being:
Thanks, glad to know I was on some kind of correct path. I’m going to re-immerse myself in the algebra way, but before I do that. I see where I missed the negative. So when I got the derivative, I plugged in my value for x which I concluded was 2. So to make -2x + 4 = 1, would have to mean my x = 1.5?
so..
m = 1
x = -4/2(-1) = 2
y = -4 + 8 – 8 = -4
y + 4 = 1(x – 2)
y = x – 6
and that’s the end of it, what do I do next to come up with -23/4 naturally? Thanks
It isn’t clear what the work here means; it looks to me now like finding the vertex of the parabola \(-x^2 + 4x – 8\) using the formula \(\displaystyle\frac{-b}{2a}\), and then finding the line through that point with slope 1. The value 1.5 is correct, but has not been used.
I answered,
Yes, the parabola has slope 1 at x = 3/2, not 2. In your work here, you still show finding x = 2 and using that to find y. Instead, let x = 1.5 and determine y from that, then write the equation of the line.
You may find it helpful to show more steps. The work to get x = 1.5 is:
y’ = 1
-2x + 4 = 1
-2x = 1 – 4
-2x = -3
x = (-3)/(-2) = 3/2 = 1.5
This is presumably what Chase did to get 1.5; showing more steps than you think you need often helps in catching (or preventing) errors, and I hoped it would help with the next steps.
Finding and using the tangent line
Chase wrote back,
I’ll try again:
m = -2(1.5) + 4 = 1
y = -(1.5) + 4(1.5) – 8 = -2.25 + 6 – 8 = -4.25
m = 1
x = 1.5
y = -4.25
y + 4.25 = 1(x – 1.5)
y = x – 1.5 – 4.25
y = x – 5.75
y = x – 23/4
Having found slope intercept form, I don’t really know how to compare it to the value of k.
Looking at y = x + k, k would at least be a value of 1, I would think. But 1 < -23/4 is wrong.
How do we solve for k?
Here Chase has correctly found the tangent line; it is the red line in the first graph above. Chase has first checked that the slope is indeed 1 at this point, then found y on the parabola, and then used point-slope form to find the equation of the line. The only problem is in applying this to the problem. We need to find all values of k for which the line \(y=x+k\) intersects the parabola exactly twice, and we have found that the line \(y=x-\frac{23}{4}\) intersects the parabola exactly once. Chase seems to be confusing k, the y-intercept, with the slope, 1. How can we see the conclusion?
I decided that a visual approach would be helpful, and wrote back:
Hi, Chase.
Here is a graph I made showing the parabola (blue), the tangent line y = x – 23/4 (red), and an arbitrary line y = x + k (green).
For what values of k will the line intersect the parabola in two points?
Here I showed that a line above the tangent will not intersect the parabola at all, which is true because the parabola, having a negative leading coefficient, opens downward. In contrast, any line below the tangent (that is, with \(k<-\frac{23}{4}\)), will intersect twice, so that is the solution.
We were finished.