(A new question of the week)
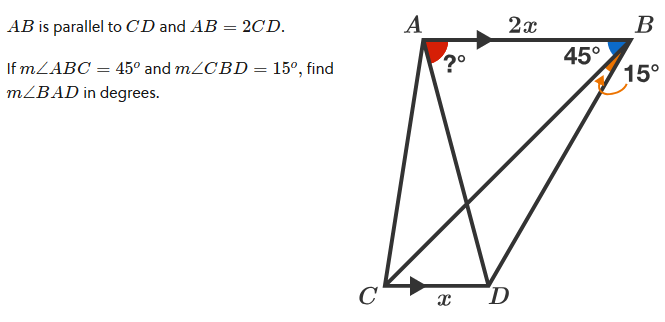
Usually when we have a figure labeled with some lengths and angles, we can expect to find unknown angles using trigonometry. When we are expected to do this using geometry alone, we can expect that there is something special about the figure that makes it possible. But how to find that specialness? That’s what we face here.
The problem
The problem came to us in early October from Abishek:
I’m not knowing how to start to solve the question?
The figure is nicely labeled to show the parallel lines and the length relationship between AB and CD, as well as the two known angles. Without any instructions or context, it looked like a nice trigonometry problem. I tried out both ways, then answered, giving minimal hints to a trig solution, but expecting that geometry might be the required method (because it was posted under Geometry, not Trigonometry!):
Hi, Abishek.
I can solve it using trigonometry, and find a simple, exact angle. So my first question to you is, are you allowed to use trigonometry, or does your solution have to use synthetic geometry?
My method using trig involves drawing auxiliary vertical lines through points B and D, from line AB to line CD perpendicularly. I called the lengths of these y, and found y as a function of x, then found the tangent of the unknown angle.
If you can use only geometry, which seems quite likely, I have some possible ideas to start with, though I have not completed them. One is to join the midpoint of AB to C. (Possibly it could be joined to D instead; either will result in a parallelogram.) I think there are many interesting relationships in the figure that, if proved, could lead to a solution.
Please pick some way to start, and show your work as far as you can get, so we can discuss it further.
Solving it with trigonometry
We won’t be pursuing the trig solution in the discussion, so let’s take a look at it now:
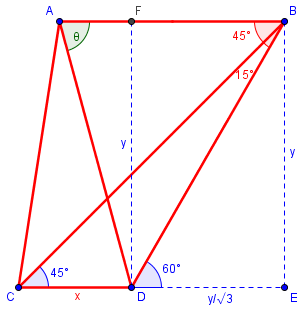
By alternate interior angles, we find that ∠BCE = 45° and ∠BDE = 60°.
From 30-60-90 triangle ΔBDE, DE = \(\frac{y}{\sqrt{3}}\). This is also the length of FB.
From right isosceles triangle ΔBCE (because of the 45° angle), we see that CE = BE = y, so \(y=x+\frac{y}{\sqrt{3}}\).
Solving for y, we find that $$x=\left(1-\frac{1}{\sqrt{3}}\right)y=\frac{\sqrt{3}-1}{\sqrt{3}}y$$ so $$y= \frac{x\sqrt{3}}{\sqrt{3}-1} = \frac{3+\sqrt{3}}{2}x$$
Now, $$\text{AF}=\text{AB}-\text{FB}=2x-\frac{y}{\sqrt{3}} = \left(2-\frac{1+\sqrt{3}}{2}\right)x=\frac{3-\sqrt{3}}{2}x$$
Finally, from right ΔAFD, $$\tan(\theta)=\frac{y}{\text{AF}}=\frac{\frac{3+\sqrt{3}}{2}x}{\frac{3-\sqrt{3}}{2}x}=\frac{3+\sqrt{3}}{3-\sqrt{3}}=2+\sqrt{3}\approx 3.732$$
So \(\theta=\tan^{-1}(3.732) = 75°\).
Getting this apparently exact and “nice” angle suggested it could be solved geometrically. (It is a common exercise in trig classes to find the exact value of \(\tan(75°) = \tan(30° + 45°)\), so we know it is in fact exact.)
First thoughts using geometry
Abishek replied as expected:
Hi Dr.Peterson, thanks for replying
Yes, we should proceed in Geometry.
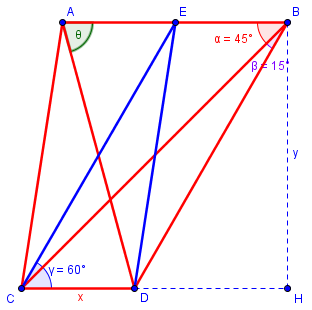
I have joined the midpoint of AB to C.
How do we proceed to the Next Step?
I had been working on the problem, but so far could only show the additional lines I had introduced:
I don’t yet see a purely geometrical solution. But here is my drawing, showing where I added two broken lines to use in the trigonometrical solution, and the two solid blue lines I think may be of use geometrically. I’m looking for some similar triangles that might be used to determine parts of the angle θ that we want to find.
I’ll keep looking as I have time.
The parallelograms seemed useful; I hadn’t needed them in the trigonometric solution, but they seemed like a good way to make use of the 2x. The perpendicular lines also seemed likely to be useful in this approach. And similar triangles are often a good way to find angles.
At this point, I’m just playing with ideas. Many of them will turn out to be dead ends; that is not unusual in problem-solving! And I like being able to show students this messy process behind solving problems, as well as the mere fact that I don’t see solutions immediately; too often textbooks make math look too neatly packaged, resulting in students feeling that if they don’t see the whole answer at once, they just can’t do mathematics.
Better ideas
Meanwhile, Doctor Rick had been looking over our shoulders, so to speak, and he jumped in with some new ideas:
Hi, Abishek. I too have been trying to solve this problem. It has the “feel” of a contest problem — it surely takes some creative thinking to find a solution! I hope you realize that it isn’t a matter of following some standard set of steps, but rather about exploring, trying a lot of things to see if they lead you anywhere. Both Doctor Peterson and I (and maybe others) are doing just this.
I drew in the lines that Doctor Peterson showed you; one thing they do for us is to create two “special triangles”, a 45-45-90 (right isosceles) triangle and a 30-60-90 triangle. You might look for other triangles of these types that you could make by adding other lines. We don’t want to make the diagram too complicated, but I think that one more line will do the trick. (I too started by adding the lines from the midpoint of AB to C and D, but I wasn’t getting anywhere with that idea, so I got rid of those lines. Sometimes we have to let go of our first idea in order to make progress.)
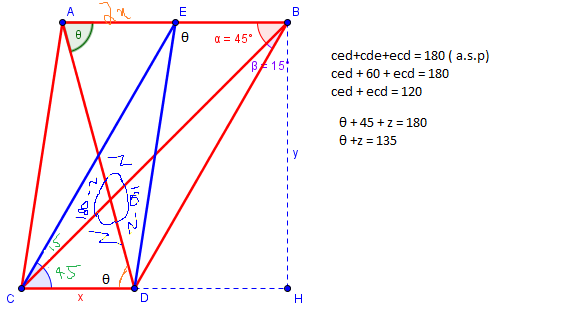
Here’s another thought. One of the facts we know involves the ratio of lengths of two segments. How can this provide information about angles, without bringing trigonometry into the picture? I can think of only one way: If we can show that two sides of some triangle are equal in length, then we know the triangle is isosceles, so its base angles are equal.
He’s saying my solid blue lines didn’t help, but something else will, something involving forming a special triangle. His wording suggested to me that he might be closer to a solution than he said!
Now Abishek, too, showed his progress, including additions to my drawing:
I have tried modifying the picture and I got this.
I’ll have to look for more things tomorrow because it’s night over here.
I had thought of working with the triangles he labeled, too, but couldn’t find a way to use them.
A geometrical solution
While Abishek slept, I found an answer and wrote back:
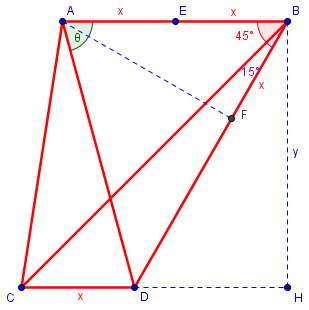
I suspect that Doctor Rick has actually solved the problem, as I now have as well. I’m going to add one more hint, namely the one additional line I used, AF:
I labeled one new length; if you label other lengths, one by one, you should be able to write an equation or two that will finish the problem.
By the way, we really could as well have called x “1”, since the unit is arbitrary; then we would be finding the actual lengths of many segments.
The new line AF is drawn perpendicular to BD, though not marked as such. (I’d also considered drawing a perpendicular to BC, but that didn’t seem to lead anywhere.) I wrote in the length of BF as x because seeing that was the key to my solution. I hoped this was a small enough hint not to spoil the fun of the final chase!
Abishek was unsure of the reason for one label on the diagram:
Then, how did we find length of BF to be x?
That was a good question; I answered,
Because AF was constructed perpendicular to BD, and angle ABF = 60°, triangle ABF is a 30-60-90 triangle (half on an equilateral triangle). That makes BF half of AB.
I included that on my diagram because, although it is “obvious”, I initially missed it; when I included that fact, I knew I could solve the problem!
I could also have labeled AF as \(\sqrt{3}x\), due to the same triangle, but the x was the key.
This was the end of our discussion. I assume Abishek was able to finish with these hints. But we haven’t seen the end yet, so let’s do it now:
We can start as with the trig solution, finding y: $$y= \frac{3+\sqrt{3}}{2}x$$
Then, in 30-60-90 ΔBDH, $$\text{DB}=2\text{DH}=\frac{2}{\sqrt{3}}y = (1+\sqrt{3})x$$
Therefore, $$\text{DF}=\text{DB}-\text{BF}=(1+\sqrt{3})x-x=\sqrt{3}x$$
But this is equal to AF (in 30-60-90 triangle ΔABF), so ΔADF is a right isosceles triangle, and ∠FAD = 45°.
So we can conclude that ∠BAD = ∠FAD + ∠FAB = 45° + 30° = 75°. We are finished!