In looking into combinatorics for last week, I ran across several questions about the topic of “derangements” (permutations of objects in which none of them are in their original positions). Let’s look at those, first at probability, and then at the closely related matter of counting. This will also bring us to the Inclusion-Exclusion Principle.
Probability that nothing is in the right place
We’ll start with a question from Raveen in 1998:
Probability of Matching Envelopes and Letters Six letters were to be placed in envelopes for posting. Unfortunately, the letters were dropped before being put in their envelopes, and they were placed in at random. a) What is the probability that none is in the correct envelope? b) What is the probability that exactly one is in the correct envelope? Answers a) 53/144 b) 11/30
Part (a) is the classic example of derangements: arrangements in which everything is in the “wrong” place. To illustrate it in a much simpler case, if we had only three letters, then there would be 6 ways to arrange them:
ABC ACB BAC BCA CAB CBA
Of these, one (ABC) has all three in the right place; none have exactly two in the right place; three (ACB, BAC, and CBA) have exactly one in the right place, and two (BCA, CBA) have none in the right place. These last two are the derangements. So the number of derangements is 2, and the probability of a derangement is 2/6 = 1/3. The formula we’ll be seeing gives this probability: $$\frac{1}{2!}-\frac{1}{3!}=\frac{1}{2}-\frac{1}{6}=\frac{1}{3}=0.3333\dots$$
Doctor Anthony answered, starting with a similar problem (5 rather than 6 items):
I answered a nearly identical question earlier today, so I will copy that answer here. I was considering 5 letters and 5 envelopes. If we let A be the event that letter A is in its correct envelope and similarly B is the event that letter B is in its correct envelope, then P(A) = 1/5 and P(A and B) = 1/5 * 1/4
This is because there are 5 places to put A, one of which is correct; and once A is in place, there are 4 places to put B, one of which is correct.
The probability that either A or B is in the right place is $$P(A\text{ or }B)=P(A)+P(B)-P(A\text{ and }B)=\frac{1}{5}+\frac{1}{5}-\frac{1}{20}=\frac{7}{20}$$ This is a simple case of the Inclusion-Exclusion Principle, which will be explained later.
Now use the inclusion-exclusion principle to get probability that A or B or C .... or E are correctly placed.
P(A or B or C .... or E) = P(A) + P(B) + P(C) + P(D) + P(E)
- P(A and B) - P(B and C) -....
+ P(A and B and C) + P(B and C and D) + ....
- P(A and B and C and D) - P(...) -......
+ P(A and B and C and D and E)
= 5*(1/5)
- 5C2*(1/5)(1/4)
+ 5C3*(1/5)(1/4)(1/3)
- 5C4*(1/5)(1/4)(1/3)(1/2)
+ (1/5)(1/4)(1/3)(1/2)(1/1)
5*4 1 5*4*3 1 5*4*3*2 1 1
= 1 - --- * --- + ----- * ----- - --------- * ------- + ---------
1*2 5*4 1*2*3 5*4*3 1*2*3*4 5*4*3*2 5*4*3*2*1
= 1 - 1/2! + 1/3! - 1/4! + 1/5!
This is the probability that at least one letter is correctly placed.
This is the complement of what we want: If it is not true that at least one is right, then none are right:
The chance that none is correctly placed is 1 - (above result), or = 1 - 1 + 1/2! - 1/3! + 1/4! - 1/5! = 1/2! - 1/3! + 1/4! - 1/5!
This is the formula we want, applied to the case of 5 items. the result is \(0.5-0.1667+0.4167-0.0083=0.3667\).
The same thinking applies in general:
With n letters and envelopes, the probability that none is correctly placed is:
= 1/2! - 1/3! + 1/4! - 1/5! + ....... + (-1)^n 1/n!
Note that as n becomes very large, this probability tends to the value e^(-1), since:
e^(-1) = 1 - 1 + 1/2! - 1/3! + 1/4! - ........ to infinity
= 0.367879...
You may recall that e is a special number, approximately 2.71828, that arises in calculus and in finance. We discussed this number in Where Do Logarithms Come From?, and in Equivalent Definitions of e. These include the formula for any power of e, $$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots$$ When \(x=-1\) this gives the formula Doctor Anthony showed. We’ve seen that the probabilities for \(n=3\) and \(n=5\) are respectively 0.3333 and 0.3667, which are already getting quite close to 0.367879.
Putting the result as a formula, the probability of a derangement of n items is $$\sum_{k=2}^{n}\frac{(-1)^k}{k!}.$$ And since the terms for \(k=0\) and \(k=1\) add up to 0, we can just as well call it $$\sum_{k=0}^{n}\frac{(-1)^k}{k!}.$$
(Oddly, though, this implies that there is one derangement of an empty set – but, appropriately, none for a set of one element.)
How about Raveen’s question? Just apply the general formula:
With six letters and envelopes, the probability that none is correctly placed is: = 1/2! - 1/3! + 1/4! - 1/5! + 1/6! = 1/2 - 1/6 + 1/24 - 1/120 + 1/720 = 53/144.
This is 0.368055… .
Part (b) of the question will build on everything we’ve seen:
To find the probability that exactly one is correctly placed, we need to find the total number of ways with 1 correct and 5 incorrect.
We can use the result of the last problem to see the number of ways where 5 letters are all incorrect.
If we had 5 letters and 5 envelopes, the probability that all are incorrect is 1/2! - 1/3! + 1/4! - 1/5!
Therefore the number of arrangements with all incorrect is given by
5!(1/2! - 1/3! + 1/4! - 1/5!) = 44
Here, we multiplied by the total number of arrangements. We’ll be calling this \(D(5)\).
Now imagine the letters laid out in a row, and the envelopes in a matching row.
If the first letter is the only correct one opposite its envelope, then there are 44 arrangements for the other 5 all putting them in the incorrect envelope. Similarly, if the second one is the only correct one, then this can be associated with 44 arrangements for the other 5, which will all be incorrect. Similarly, for third, fourth, fifth and sixth letters, they can each be associated with 44 arrangements, making the other 5 all incorrect.
So the total number of arrangements in which just one is correctly placed is:
6 x 44 = 264
The total number of possible arrangements is of course 6! = 720, so the probability that exactly one is correct is
264/720 = 11/30
Generalizing, the probability that exactly one letter of n is correctly placed is $$\frac{n\cdot D(n-1)}{n!}=\frac{D(n-1)}{(n-1)!}$$ where \(D(n)\) is the number of derangements of n objects; using our formula, this becomes $$(n-1)!\sum_{k=0}^{n-1}\frac{(-1)^k}{k!}\cdot\frac{1}{(n-1)!}=\sum_{k=0}^{n-1}\frac{(-1)^k}{k!}.$$
For our case of \(n=6\), that’s $$\sum_{k=0}^{5}\frac{(-1)^k}{k!}=\frac{44}{120}=\frac{11}{30}.$$
More on the Inclusion-Exclusion Principle
A year later, Doctor Anthony wrote a very similar answer, and included the following on the Inclusion-Exclusion Principle:
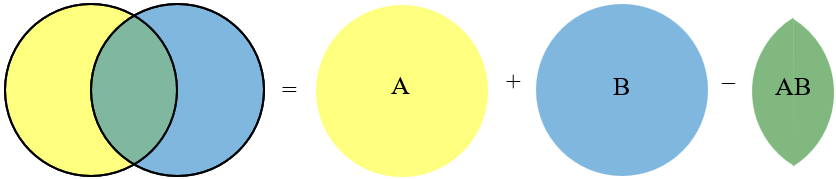
Letters and Envelopes - the Inclusion-Exclusion Principle We can use a Venn diagram to illustrate the principle with two or three probabilities. For example: with two overlapping probabilities P(A), P(B), we have P(A or B) = P(A) + P(B) - P(A and B) The overlapping region is accounted for once with P(A) and again with P(B), so to account for it once only we subtract P(A and B), giving rise to the expression shown above.
We have to subtract the green region, which was counted as part of both A and of B, so it’s counted only once:
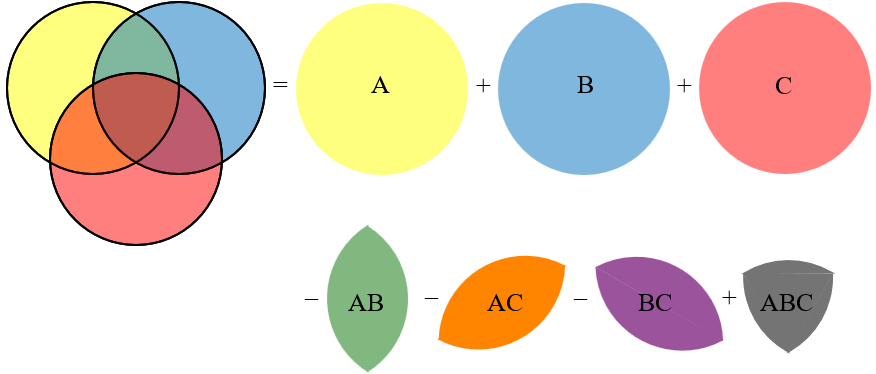
With three overlapping probabilities P(A), P(B) and P(C) we get
P(A or B or C) = P(A) + P(B) + P(C)
- P(A and B) - P(B and C) - P(C and A)
+ P(A and B and C)
now the overlap of all 3 probabilities is added 3 times by the first line of this equation, subtracted 3 times by the second line of the equation and so must be added again by the third line.
The area corresponding to A and B but not C is added twice in the first line and subtracted once in the second line, so it will appear once, as is required. The same is repeated for area B and C but not A, and the area corresponding to C and A but not B, so each will eventually appear once only.
With more probabilities, the pattern continues, and the proof by induction is not difficult but a little tedious. The name 'inclusion-exclusion' describes exactly what is happening: regions are being added a number of times and subtracted a number of times in such a way that each region occurs exactly once.
We have to subtract the overlaps of two circles, but then add back on the overlap of all three:
We could prove this fact by repeatedly applying the “or” formula: $$P(A\text{ or }B)=P(A)+P(B)-P(A\text{ and }B)$$
$$P((A\text{ or }B)\text{ or }C)=P(A\text{ or }B)+P(C)-P((A\text{ or }B)\text{ and }C)\\=\left [ P(A\text{ or }B)+P(C) \right ]-P((A\text{ and }C)\text{ or }(B\text{ and }C))\\=\left[P(A)+P(B)-P(A\text{ and }B)+P(C)\right]-\left[P(A\text{ and }C)+P(B\text{ and }C)-P((A\text{ and }C)\text{ and }(B\text{ and }C))\right]\\=P(A)+P(B)-P(A\text{ and }B)+P(C)-P(A\text{ and }C)-P(B\text{ and }C)+P(A\text{ and }B\text{ and }C)\\=P(A)+P(B)+P(C)-P(A\text{ and }B)-P(A\text{ and }C)-P(B\text{ and }C)+P(A\text{ and }B\text{ and }C)$$
This suggests how induction could work.
Counting derangements
We’ll spend the rest of our time with this question from 1997 about counting, rather than probability, where we’ll fill in some details:
Word Derangements and Arrangements Hi Dr. Math, I have to write this paper on derangements but I'm a little stuck. First you have to find the arrangements on let's say a 3 letter word, JOE. JOE has 6 arrangements: J,O,E J,E,O O,J,E O,E,J E,J,O E,O,J. Now to find the derangements, you have to put the letters in alphabetical order, which is E J O. This means that E cannot be the 1st letter, J cannot be the 2nd letter, and O cannot be the 3rd letter. Since there are only two arrangements that meet this criterion, JOE has 2 derangements, J,O,E and O,E,J. I figured out all the derangements for 2, 3, 4, and 5 lettered words by listing them, but when I got up to the 6th lettered word, I got stuck because a 6 lettered word has 720 arrangements. It'll be impossible for me to list all the derangements. Is there a formula that I can use to find the derangements of arrangements?
Here a derangement has been defined relative to alphabetical order rather than the original order, but the idea is the same. It matches my initial example above with ABC. For larger numbers, counting by hand becomes unwieldy. Is there a formula? We saw one for probability, and we saw in passing a formula for counting as well:
Doctor Rob answered:
Yes, there is. The formula is:
D(n) = n! - n!/1! + n!/2! - n!/3! + n!/4! - ... + (-1)^n*n!/n!
When n = 6, this gives:
D(6) = 720 - 720 + 720/2 - 720/6 + 720/24 - 720/120 + 720/720
= 720 - 720 + 360 - 120 + 30 - 6 + 1
= 265
This formula is just the probability formula multiplied by n!, just as Doctor Anthony did. Here the probability is 265/720 = 0.368055… .
This formula, like the other, can be obtained directly by inclusion-exclusion:
This formula is gotten by starting with the n! arrangements, then subtracting those with one object fixed, C(n,1)*(n-1)! = n!/1!, then adding those with two objects fixed, C(n,2)*(n-2)! = n!/2!, because they had been subtracted twice. Then we subtract those with three objects fixed, C(n,3)*(n-3)! = n!/3!, because they had been subtracted thrice, but added back in thrice. We continue thus until we run out of objects.
This is a very brief summary of the derivation; we’ll examine it more slowly below.
A short way to compute this is to pick the closest integer to n!/e. Here e is the base of natural logarithms, 2.718281828459045.... If n = 6, this gives 720/2.718281828459045... = 264.8731976..., so D(6) = 265, the same answer we got above. The first few answers are 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, and 1334961.
This is related to what we saw above, that the probabilities approach 1/e; but this time we’re looking for a whole number count, and it happens that rounding gives the exact value. Here are the exact and rounded values for \(\frac{n!}{e}\) for n up to 14:
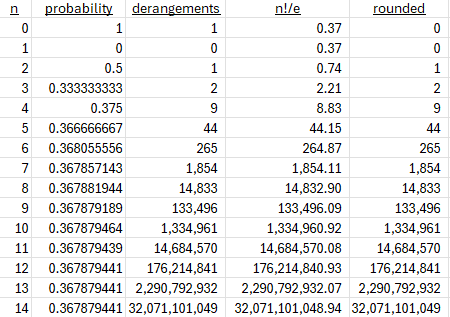
Observe how quickly the probability approaches 1/e, and that the rounded values do exactly match the number of derangements, even for small numbers.
Explaining and illustrating the derivation
Julie wanted a fuller explanation:
Hello Dr. Math, I wrote to you before to ask if there was a formula to find the derangements of arrangements. You replied by sending me this formula: D(n) = n! - n!/1! + n!/2! - n!/3! + n!/4! - ......+ (-1)^n*n!/n! I understand how to use the formula, but I'm not sure how to derive it. You gave me an explanation, but it was a bit confusing. Can you please explain it again? Thank you!
Doctor Rob answered in more depth:
This is an application of the Inclusion-Exclusion Principle. We want to know the number of arrangements with exactly zero items in the designated spots. That is D(n). We can count the number C(n,k) of ways to choose k spots out of n to be designated; then there are (n-k)! ways to arrange the other n-k letters. This makes a total of C(n,k)*(n-k)! = n!/k!. This is, however, more than the number of arrangements with k items in their designated spots, since some arrangements are counted more than once.
That is, $${n\choose k}\cdot(n-k)!=\frac{n!}{k! (n-k)!}\cdot(n-k)!=\frac{n!}{k!}$$ gives the number of ways to arrange n letters with k specified letters in the right places (and possibly others as well); but for any particular case, we might have counted the same arrangement by specifying a different set of k first.
We start with all the arrangements; that is, those with at least zero items in the designated spots. There are n!/0! = n! of them. From this number we subtract the number we computed above, n!/1!. This is too much to subtract, because there are arrangements with two items in their designated spots which are counted twice, once for each of the two. To compensate, we add back in the then number of arrangements with two or more items in the designated spots, namely n!/2!. But we have overcompensated, so we subtract the number of arrangements with three or more items, and so on.
This begs for a concrete example!
Example: RUST, alphabetically RSTU. There are 4! = 24 arrangements: RSTU, RSUT, RTSU, RTUS, RUST, RUTS, SRTU, SRUT, STRU, STUR, SURT, SUTR, TRSU, TRUS, TSRU, TSUR, TURS, TUSR, URST, URTS, USRT, USTR, UTRS, UTSR. There are C(4,1) = 4 ways to pick a single letter to be in its designated spot, and for each, there are (4-1)! = 3! = 6 ways to rearrange the other letters, for a total of 4*6 = 24 = 4!/1!: R fixed: RSTU, RSUT, RTSU, RTUS, RUST, RUTS S fixed: RSTU, RSUT, TSRU, TSUR, USRT, USTR T fixed: RSTU, RUTS, SRTU, SUTR, URTS, USTR U fixed: RSTU, RTSU, SRTU, STRU, TRSU, TSRU We have to discard these, but some of them appear twice (or more). To compensate, we add back in the number of arrangements with two letters in their designated spots. There are C(4,2) = 6 ways to pick two letters to be in their designated spots, and for each there are 2! = 2 ways to rearrange the other letters, for a total of 6*2 = 12 = 4!/2!: R,S fixed: RSTU, RSUT R,T fixed: RSTU, RUTS R,U fixed: RSTU, RTSU S,T fixed: RSTU, USTR S,U fixed: RSTU, TSRU T,U fixed: RSTU, SRTU Now we have overcompensated, since some arrangements with two letters fixed also have three letters fixed, so we have to subtract the number of these to compensate. There are C(4,3) = 4 ways to choose the three letters to be in their designated spots, and for each there is 1! = 1 way to rearrange the other letter, for a total of 4*1 = 4 = 4!/3!: R,S,T fixed: RSTU R,S,U fixed: RSTU R,T,U fixed: RSTU S,T,U fixed: RSTU Again, we have overcompensated, since some (actually all) arrangements with three letters fixed also have four letters fixed, so we have to add back in the number of these to compensate. There is C(4,4) = 1 way to choose the four letters to be in their designated spots, and for each there is 0! = 1 way to arrange the remaining zero letters, for a total of 1*1 = 1 = 4!/4!: R,S,T,U fixed: RSTU That makes the total: D(4) = 4!/0! - 4!/1! + 4!/2! - 4!/3! + 4!/4! = 24 - 24 + 12 - 4 + 1 = 9
So what happened to each arrangement?
The arrangement RSTU with four letters fixed was counted once in the original tally, subtracted four times, added six times, subtracted four times, then added once, for a net count of 0. There are no arrangements with exactly three letters fixed. You can verify each arrangement with exactly two letters fixed was counted once, subtracted twice, and added once, for a net count of 0. You can verify each arrangement with exactly one letter fixed was counted once, and subtracted once, for a net count of 0. All those with no letter fixed were counted once and never subtracted, for a net count of 1. For any arrangement with exactly k > 0 letters fixed, the net count is C(k,0) - C(k,1) + C(k,2) - ... = (1-1)^k = 0, by the Binomial Theorem.
We saw the Binomial Theorem in Fibonacci, Pascal, and Induction; it says that $$(x+y)^n = \sum_{k=0}^n{n\choose k}x^{n-k}y^k.$$ Here, if we let \(x=1\) and \(y=-1\), we get $$(1-1)^n = \sum_{k=0}^n{n\choose k}(1)^{n-k}(-1)^k={n\choose 0}-{n\choose 1}+{n\choose 2}-…+(-1)^n{n\choose n},$$ and this equals zero.
Illustrating the formula inside-out
20 years later, in 2017, reader Thayer asked for further clarification:
I understand that the inclusion-exclusion formula for n = 4 gives the proper 9 derangements. But I don't understand the meaning of the terms when applied to the set {1, 2, 3, 4}.
In particular, I can't figure out the actual arrangements in its terms.
Put another way: The number of derangements with 3 fixed elements is 4C3*1! = 4. But if 3 elements are fixed, there is only one choice for the 4th element.
What are the 4 derangements of {1234} that have three elements fixed? Isn't there only one -- namely, 1234?
He means 4 arrangements; but his main difficulty is probably with the meaning of “fixed”.
I answered:
Hi, Thayer.
I suppose you are referring to a variation of the formula above:
D(n) = n! - n!/1! + n!/2! - n!/3! + n!/4! - ... + (-1)^n*n!/n!
Your version, though you didn't state it, is the unsimplified form of the same formula.
That is, his “4C3*1!” is Doctor Rob’s “C(n,k)*(n-k)! = n!/k!.” That is probably what he was asking about.
In your case, n = 4, and we have
D(4) = 4! - 4!/1! + 4!/2! - 4!/3! + 4!/4!
= 24 - 24 + 12 - 4 + 1
= 9
The first term is the total number of possible arrangements; the second is the number of those with some one element fixed (i.e., A fixed, or B fixed, or C fixed, or D fixed, so that those with at least two fixed are counted twice); the next is the number of those with some pair of elements fixed (AB, AC, AD, BC, BD, or CD), and so on.
I think this clarifies Doctor Rob’s “one element fixed” to show that it means we have chosen some one element to be in place, not that exactly one element is in place.
Now I illustrated what happens to each arrangement at each step:
Let's make a table showing the arrangements counted in each term. To avoid confusing an element with a number of elements, I'm going to use letters (ABCD) rather than digits (1234). This also lets me put an element in lower case when it is in its place, to make them easy to see.
# fixed --> 1 | 2 | 3 | 4
------------------- ----------------------------- ------- -----
all| A B C D AB AC AD BC BD CD (any 3) (all 4)
----|---- ---- ---- ---- |---- ---- ---- ---- ---- ----|-------|-----
abcd abcd abcd abcd abcd abcd abcd abcd abcd abcd abcd abcd*4 abcd
abDC abDC abDC abDC
aCBd aCBd aCBd aCBd
aCDB aCDB
aDBC aDBC
aDcB aDcB aDcB aDcB
BAcd BAcd BAcd BAcd
BADC
BCAd BCAd
BCDA
BDAC
BDcA BDcA
CABd CABd
CADB
CbAd CbAd CbAd CbAd
CbDA CbDA
CDAB
CDBA
DABC
DAcB DAcB
DbAC DbAC
DbcA DbcA DbcA DbcA
DCAB
DCBA
---- ---- ---- ---- ---- |---- ---- ---- ---- ---- ----|-------| ----
24 6 6 6 6 2 2 2 2 2 2 4 1
---- ------------------- |-----------------------------|-------| ----
24 24 12 4 1
The main idea is that when we say we are counting "arrangements with one object fixed," what we really mean is "arrangements with x fixed, for each possible x." This counts many arrangements twice, so we have to subtract those duplicates.
Each of the 24 rows shows each time we count one arrangement. The first column lists all permutations. In each subsequent column, the heading is a set of letters that have been chosen to be in their places, which I have put in red; all letters that are in place are in lower case.
If you look at each row with any lower case, you can see that additions and subtractions end up with 0; for example, the row
# fixed --> 1 | 2 | 3 | 4
------------------- ----------------------------- ------- -----
all| A B C D AB AC AD BC BD CD (any 3) (all 4)
----|---- ---- ---- ---- |---- ---- ---- ---- ---- ----|-------|-----
CbAd CbAd CbAd CbAd
shows that we add 1, subtract 2, and add 1, for a total of 0. But the 9 rows with nothing in place have only one entry, which is counted in the total of derangements, \(24-24+12-4+1=9\).
The entry “abcd*4” represents 4 entries, “abcd abcd abcd abcd” corresponding to the header “ABC ABD ACD BCD”. That’s the specific case Thayer asked about:
In the column above that enumerates 3 fixed arrangements, abcd is counted four times (once each for ABC, ABD, ACD, and BCD), which I didn't bother breaking out into four sub-columns. This is what you were specifically asking about: yes, there is only one such arrangement. But we count it four times, once for each possible choice of 3. I liked your idea of listing everything explicitly, which is why I wrote more than just the one paragraph above. A table does make the whole idea a lot clearer. What do you think?
We didn’t hear back. I hope my addition of color makes it a little easier to understand.
