A recent question involved the Pigeonhole Principle; we’ll start with an older question to introduce the idea, then the new question and a few old ones.
Rest areas on a path
We’ll start with this, from September 2020:
I am required to solve the following problem by use of the Pigeon-hole Principle:
A bicycle path is 30 miles long, with four rest areas. Prove that either there are two rest areas that are at most six miles from each other, or there is a rest area that is at most six miles away from one of the endpoints of the path.
Pigeon-hole Principle:
Let n and k be positive integers, and let n > k. Suppose we have to place n identical balls into k identical boxes. Then there will be at least one box in which we place at
least two balls.
To illustrate the principle, here is the case \(n=5,k=4\), that is, 5 balls and 4 boxes:
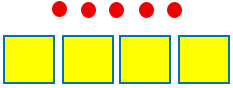
No matter how you try to place the balls, since there are more balls than boxes, you will always have at least one box containing at least 2 balls:
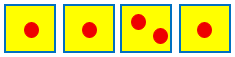
There could be more than two balls in a box,

or more than one such box,
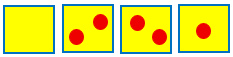
But you can never have only one ball per box.
This is obvious, because if you were trying your best to get no more than one per box, once you’ve used all k boxes, you’re forced to put a second one somewhere. But, as we’ll see, it can be powerful in problems that are much less obvious.
The fun comes when there aren’t literal balls and boxes, and you have to model a problem in that way for yourself.
By the way, in the original formulation, the image was of objects in “drawers”, or in “pigeonholes” used for sorting mail and the like. (I have an old desk with such pigeonholes in the room I’m working in.) But the common use of the term “pigeonhole” by people less familiar with such a desk has led to people talking about “pigeons in pigeonholes” (nests), which is more memorable than “balls in boxes”.
So how does this relate to a 30-mile path with 4 rest areas (and two end points)?
![]()
I answered with three hints:
Hi, Nohad.
You might consider dividing the 30-mile path into 6-mile segments.
What would be the “balls”? What would be the “boxes”?
You might also find that you want to imagine some extra rest areas!
Here is the path divided into 6-mile segments:
![]()
And here is my example superimposed on the segments:
![]()
If you think of endpoints (red dots) as additional rest areas, the problem is to show that at least two of the 6 dots are 6 miles or less from one another. We can see that two pairs of dots are that close; one pair are within the same marked segment, though the other are not. (Not all pairs that are less than 6 miles apart are in the same segment, but it will be sufficient that any pair in the same segment must be that close.)
Unfortunately, though Nohad read this, he never replied. Possibly he was hoping for a complete answer, and didn’t want to work with us; or these hints may have been all he needed! But this will give us a chance to look at the method in a very simple case (which happens to lead directly to our new problem).
Let’s think about how the Pigeonhole Principle might apply.
Observe that there are 5 6-mile intervals, and we have a total of 6 dots (two of them in fixed locations). If any two of them are in the same interval, then they are at most 6 miles from each other; and because there are more dots than intervals, that will necessarily happen. So thinking of rest areas and endpoints as “balls“, and our 5 intervals as “boxes“, the Pigeonhole Principle proves it.
Often, the Pigeonhole Principle can be replaced by what I call worst-case thinking. Suppose we are trying to avoid having any of the dots be less than 6 miles apart, in order to prove the claim wrong. What would we do? The worst we could do it so place them like this:
![]()
But since the claim is that some have to be at most 6 miles apart (which they all are here!), in order to prevent that, we want them to me more than 6 miles apart, and have to spread them out just a little more. But there is no room to spare. So our attempt to resist the claim fails.
The phrase “at least” or “at most” in the problem is important, isn’t it? We’ll see it again.
Penguins on an ice block
Here is the recent question, from early July this year:
I was given a Pigeonhole Principle question.
The question is as follows:
A rectangular block of ice measures 8 m by 12 m. Penguins will fight any other penguin within a range of 5 m. Prove that there’s bound to be a fight if you put 9 penguins on this block of ice
For my solution, since penguins fight anything within a range of 5 m, I thought 5 m would become the radius for a circle, where anything within the circle’s area would get attacked. Therefore, I calculate the area of the circle and the area of the rectangular block of ice. Then I could make the area like the pigeonhole and see how many circle areas fit into the block of ice.
However, the problem is that the area of the block of ice is 12×8 = 96 m2 whereas each circle area covers pi(5)2 = 78.54 m2. If this is correct, then it means only one penguin can possibly fit on the block of ice. What am I doing incorrectly?
Thank you for the help
The claim is that, of 9 penguins you place anywhere in the rectangle, at least two will be within 5 meters of one another. This is a two-dimensional version of the rest area problem!
Here is the 8×12 rectangle, and the 5 meter circle around one penguin:
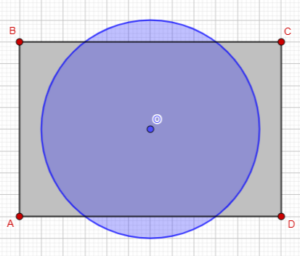
No more than one circle could fit, if they can’t overlap; but does that mean there can be only one penguin?
Doctor Rick answered:
Hi, Joash.
The problem is:
A rectangular block of ice measures 8 m by 12 m. Penguins will fight any other penguin within a range of 5m. Prove that there’s bound to be a fight if you put 9 penguins on this block of ice.
Without any work, I could see that it’s possible to get at least six penguins on the block of ice: one at each corner and one at the middle of each long edge. So you’re quite right that your initial work can’t be correct.
I can point out two things you have done incorrectly. First, if you draw a circle of radius 5 m around each penguin and require that the circles not overlap, the penguins will be at least 10 meters apart! Think about it …
Second, a penguin can be on the edge of the block of ice; it’s OK for the circles to extend beyond the edge.
When I repair your work by dealing with each of these issues, I can show that ten penguins won’t fit on the ice, but I haven’t ruled out nine penguins; I’m still thinking about how we can narrow this constraint. Let’s both keep thinking about it.
Here are 6 penguins, all at least 5 meters apart, showing their overlapping 5-meter circles:
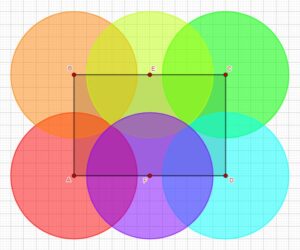
The next day, with no response yet, I added a little:
Hi, Joash.
As a further hint, in order to use the Pigeonhole Principle, you will want to divide the rectangle into 8 parts such that any two points in the same region are within 5 meters of one another. These regions don’t have to be circles containing all points within 5 meters.
There’s an interesting similarity to the previous problem. There, we saw that each “box” (interval) did not have to contain every pair within 6 miles, but that if a pair was in an interval, then they would be within 6 miles. Here, the regions don’t have to contain every point within 5 meters; but if a pair are in the same region, then they must be within 5 meters. So the regions need not be circles, but they will fit inside circles. This is a common issue in Pigeonhole Principle problems!
I had drawn a picture similar to the one above, recognizing where two more penguin could be placed, 5 meters away from any of the others:
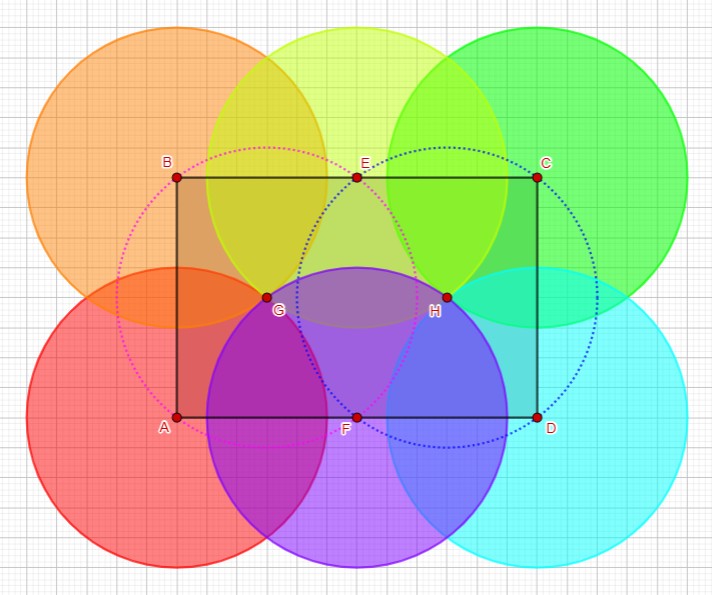
The circles overlap, but no point is inside another’s circle.
That led to recognizing some rectangles …
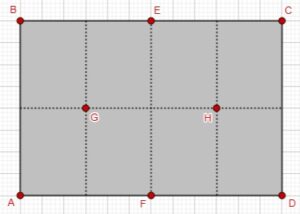
Joash eventually responded, presenting good ideas mixed with bad:
I think I have the answer now.
So the total area of the block of ice is 8×12 = 96 m2. In order to divide this up into penguin territories, we have to use the factors of 96.
Each factor pair, such as (8, 12) or (6, 16), indicates the number of Penguin Territories (8 or 6 penguin territories) and the area of each territory (12 or 16 square metres). If we choose (8, 12), we can split the into 8 regions with sides 4×3 (to guarantee maximum space for penguins). If we do the √(42+32) we find the diagonal of these 8 penguin territories to be exactly 5. This means we can fit 8 penguins by placing each penguin on opposite corners of each 4×3 territory, starting by putting a penguin on the very corner of the 12×8 block of ice.
Here I think a possible flaw is the definition of the word “within”, where if “within” is meant to include 5, so ≤ 5, then this solution wouldn’t work. However, if each penguin can be exactly 5m apart without fighting then this solution would work.
If you have 9 penguin territories, each territory would be 10.67 m2 which is < 12 m2 so we know it cannot guarantee each penguin is 5 m apart as 12 m is effectively the minimum area where this condition is fulfilled. Also, if we go with the analogy of factor pairs indicating penguin territories and areas, it is impossible to have 10.67 territories so that automatically prevents you from having 9 penguin territories on this block.
Therefore, since the maximum number of penguins that can fit on such a block is 8, according to the Pigeonhole Principle, putting 9 penguins on the block will guarantee a fight occurring.
I am wondering if the idea of factors pairs of 96 representing possible territories and areas is the correct way of thinking? Would it be valid for me to say that it is impossible to have 9 penguins solely based on the fact that 9 isn’t a factor of 96? I feel that in this question it is valid but only because 12 m2 happens to be the smallest area you can have while fulfilling the requirement for the penguins to be 5 m apart.
What do you think?
The rectangles are good, but the factor idea is not directly useful.
Doctor Rick gave some clarification:
I think you are close to the correct idea, but you are confusing yourself by referring to the rectangles as “territories“.
In regard to the matter of factors, nothing says that a “territory” must have an integral area in square meters. More important, the rectangles are not penguins’ “territories,” or “exclusion zones” for other penguins. A penguin does not care about rectangles. Rather, the rectangles are an artificial construct, created for our own purposes to allow application of the Pigeonhole Principle.
This is important: The “pigeonholes” are our idea; the penguins are not “pigeons” that care about the rectangular “hole” they are in! Thinking about bird behavior brought in the misleading idea of “territories”. which is not what the “boxes” are.
Once we divide the rectangular block of ice into eight rectangles, each 3 m by 4 m, we see that no two penguins can be in the same rectangle. This is because the rectangle fits within a circle of radius 5 m, so that any two points in the same rectangle are less than 5 meters apart. Once we have put one penguin in each of the eight rectangles, there is no place to put a ninth penguin.
Just as, in the first problem, being in the same segment was not equivalent to being less than 6 miles apart, but did imply it, here being in the same rectangle is not the only way to be less than 5 meters apart, but does imply it. And that is enough.
The dimensions of the block of ice were certainly chosen to make the problem work: We need rectangles with diagonal 5 meters or less, which partition the block exactly, in order to apply the principle. But if we couldn’t create such a partition, it wouldn’t mean that the corresponding number of penguins cannot fit, only that the Pigeonhole Principle cannot be applied.
We’ll see next time a problem where it takes several tries to find a set of “boxes” that work.
What you have said about the meaning of the word “within” is a valid point. Not only does your particular placement of eight penguins (which I suspect is the only solution) not work if “within a range of 5 m” means “at a distance less than or equal to 5 m”; the pigeonhole proof doesn’t quite work, and I don’t think it can be repaired. Thus I’m sure the intent was that the distance between penguins cannot be less than five meters, but it can be exactly five meters.
It’s also worth noting that the 8 penguins that “fit” on the ice can’t move at all! It’s not meant to be a realistic problem.
Pieces on a chessboard
Now let’s look at some older questions, starting with this from 1996:
Pieces on a Chess Board Hello, I've read some of the problems you have solved for other people and I am wondering if you can solve this problem for me: Prove that with 9 separate playing pieces, you cannot place the pieces on an 8 by 8 chess board such that the distance between any 2 pieces is always different. I appreciate your help, Hai Trung Ho
To illustrate the idea, I wanted first to place 8 pieces on a chessboard, so that no two of the distances would be the same:

But when I looked closer, I saw a pair that are the same; and when I used a spreadsheet to work out the details, I found that there are 7 pairs of distances that are the same!
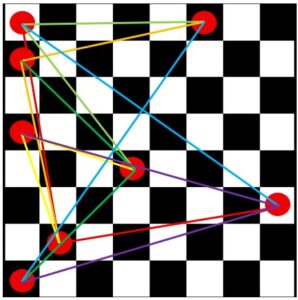
This shows how hard this can be. In fact, I’m not yet sure whether even this is possible.
So how can you prove it impossible with 9?
We’ve previously touched upon the Pigeonhole Principle in A Very Different Kind of Sequence and in A Different Kind of Chessboard Problem; the latter refers to this question.
Doctor Dennis answered:
This is a fairly tricky problem which makes use of something called the Pigeonhole Principle. The Pigeonhole Principle, in its simplest form, says that if you have n+1 balls and you are trying to put them into n boxes, then at least two balls must go into the same box.
Stop now, and think about what the balls and boxes can be. We want to show that we need at least two distances to be the same, so the boxes must represent distances; might there be more actual distances among 9 pieces, than there are possible different distances in the chessboard? We’ll have to find out.
First, consider the number of different pairs of pieces there are given that there are 9 pieces. The first piece can pair off with each of the other 8 pieces. The second piece can pair off with the 7 other pieces since it has already been paired with the first piece. The third piece can pair off with 6 other pieces, since it has already paired off with the first two. etc. There are 8+7+6+5+4+3+2+1 = 36 pairs
We could also get this as the number of combinations of 9 objects taken 2 at a time, $$_9\mathrm{C}_2=\frac{9!}{2!7!}=\frac{9\cdot8}{2\cdot1}=36.$$
As a simple illustration of this, look at how many pairs of the letters a, b, c, d there are. The pairs are:
ab ac ad 3
bc bd 2
cd 1
----------
6
Of course, the order of the pieces in the pair does not matter, since the distance between piece 1 and piece 2 is the same as the distance between piece 2 and piece 1. This is why in the example we only need to count ac and not ca as well.
This illustrates the combinations of 4 letters taken 2 at a time, $$_4\mathrm{C}_2=\frac{4!}{2!2!}=\frac{4\cdot3}{2\cdot1}=6.$$
Next, let's consider the number of possible distances on the chess board. If we place one piece in a corner, there are 35 possible non-zero distances between it and another piece somewhere on the board * 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 So to arrange 9 pieces in the indicated manner, we would have to be able to put 36 pigeons (distances between pairs of pieces) into only 35 holes (possible distances on the board). By the Pigeonhole Principle, at least 2 pairs of pieces must be the same distance apart.
This could have been calculated as 1 less than the 8th triangular number: $$\frac{8(8+1)}{2}-1=35.$$
Here he has numbered the squares on the chessboard, counting only one half of the board, because the other half would have the same distances. The distances from * to each of these positions will include all possible distances between any two squares; note that some of them are actually the same distance (in fact, from * to either 15 or 13 is 5 units, and from * to either 29 or 20 is \(5\sqrt{2}\) units), so what this actually tells us is that the number of possible distances is no more than 35. But that’s enough: we have more “balls” (actual distances between pieces) than “boxes” (possible distances), so at least one pair must be the same.
Points on a plane
We’ll close for now with this question from 2001:
Proof with Pigeonhole Principle Given five points on a plane with integer coordinates, prove that some pairs have a midpoint whose coordinates are also integers.
Here we’re still dealing with geometry, but it’s the coordinates that we’re interested in. To gain a sense of what is happening here, I’ve found four points with integer coordinates, for which none of the midpoints have only integer coordinates:
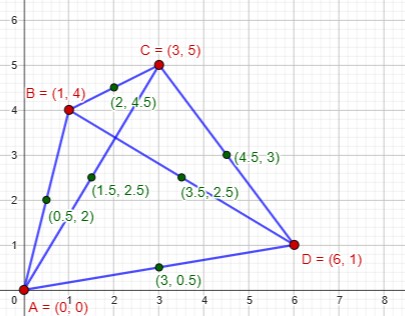
But if I try to add a fifth point, one of the midpoints always has integer coordinates, in this case the marked one at (5, 4):
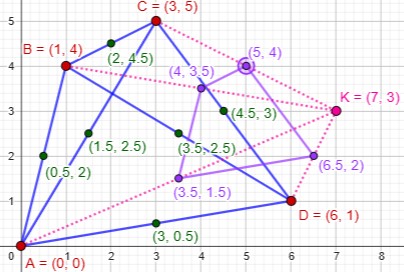
We want to prove that it’s actually impossible to avoid this, and not just difficult!
Can you see any “balls” and “boxes”? It’s not quite so obvious this time.
Doctor Floor answered:
Hi, Matt, Thanks for writing. Divide the points with integer coordinates into the following groups: 1. x odd, y odd; 2. x even, y odd; 3. x odd, y even; 4. x even, y even. I leave it to you to show that if two points are from the same group, then their midpoint has integer coordinates. From the Pigeonhole Principle it is clear that from five points, there must be two in the same group.
Below, I have colored points with integer coordinates (called “lattice points”) in four different colors to identify the four groups (green, blue, purple, red respectively):
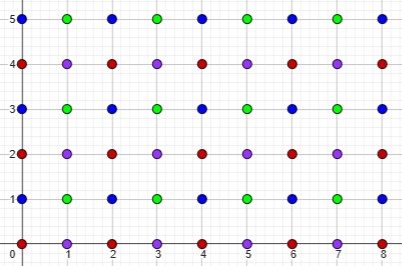
Here are a few examples of pairs of points and their midpoints:
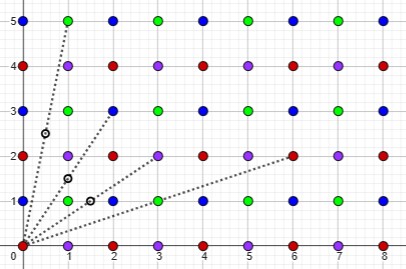
We see that the only case in which the midpoint is a lattice point is when the two points are in the same group. Why? Because in different groups, the sum of at least one coordinate will be odd (the sum of an even and an odd number), so that dividing by 2 does not produce an integer. But for points in the same group, we are always adding two odds or two evens, resulting in an even number.
So what are the balls and boxes? The boxes are the four groups of points, and the balls are the five points we choose. At least two points must be in the same group, so their midpoint will be a lattice point.
Next time, we’ll look at some more abstract applications of the Pigeonhole Principle.

Pingback: Pigeonhole Principle II: Sets, Subsets, and Sums – The Math Doctors