(A new question of the week)
Looking through recent answers we’ve given, I realized that one shares several features with my last post, as both involved proving facts using modular arithmetic and the pigeonhole principle. I need to do posts specifically about both of those concepts soon. For now, you can use the references I gave last time for information about them, or just do a search.
The challenge
Arsh sent us this problem last month, asking for advice:
Q) My question is in the attached picture.

(We prefer that you type in the question, rather than put it all in a picture, so we can search for it when necessary. But sometimes it’s helpful to see a problem exactly as given.)
I find that this comes from the (India) National Mathematics Talent Contest of 2015 for 9th grade, along with some other interesting questions Arsh has discussed with us.
I’ll reword it a little, to clarify some details:
65 bugs are placed in different squares of a 9×9 square “chess board”. Each bug moves to a horizontally or vertically adjacent square at each step; no bug makes two horizontal or two vertical moves in succession. Show that after some number of moves, there will be at least two bugs in the same square.
One ambiguity is whether one bug moves at a time, taking turns, or they all move at once, perhaps on each clock tick. I take it to be the latter, because there is no mention of taking turns. The emphasis is on the motion of each bug: each one turns left or right at each square it comes to:
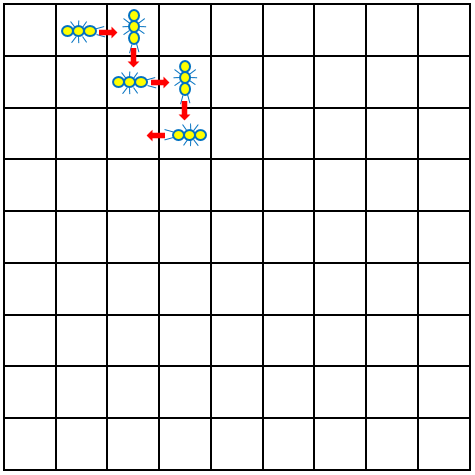
We need to guard ourselves against making additional assumptions (or at least be sure to state them when we make them). For instance, we might think that the bugs have to move in one long column snaking around the board, following one another, but that is not stated. Each bug is trying to move into an unoccupied space, but not necessarily by following the same bug that left it.
Thinking about the problem
I responded, not having yet worked out a definite solution, but offering some ideas to try:
Hi, Arsh.
This may be a good starting point:
I played with smaller boards, thinking it might be possible to prove an equivalent fact on a smaller scale. I found that if the board had an even number of squares on a side, then there could be a bug on every square, without ever having two bugs on the same square; each 2×2 group of squares could be occupied by bugs that rotate clockwise within those squares.
If there were only 64 bugs on the 9×9 board, they could do the same, using up an 8×8 region, grouped into 16 sets of 4. The 65th bug, however, can’t fit in to this pattern.
Here is a picture of a way 64 bugs could move, on an 8×8 portion of the board:
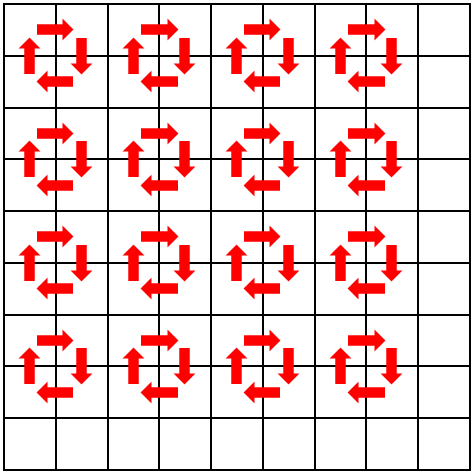
We can easily see that on a board with even dimensions (2×2, 4×4, 6×6, 8×8) there could be a bug in every square and no two would ever have to share a space (though they may not need to follow this pattern to do so). Might some other pattern work for this 9×9 board, with more than 64 bugs?
I continued:
I don’t think this can directly lead to a proof that there is no way to let 65 bugs avoid collision; but I think 4 may come into the picture.
One way to think about problems like this is to color squares. Another is to think about coordinates; on each move, one coordinate changes by 1 (changing parity, odd to even or even to odd), and after any two moves, both coordinates must change parity. That implies a constant cycling; OO->XX->EE->XX->OO.
Also, the nature of the problem strongly suggests the pigeonhole principle.
Parity refers to being odd or even, and can be thought of in terms of mod 2 arithmetic; we also referred to the pigeonhole principle last time. As I mentioned, I have seen many proofs of chessboard-type problems involving coloring the squares in an alternating pattern, and using parity. Here are a couple examples:
Covering a Checkerboard after Removing a Random Square Tiling a Mutilated Chessboard With Dominoes
Here I have colored the (odd, odd) squares red, and the (even, even) squares yellow:
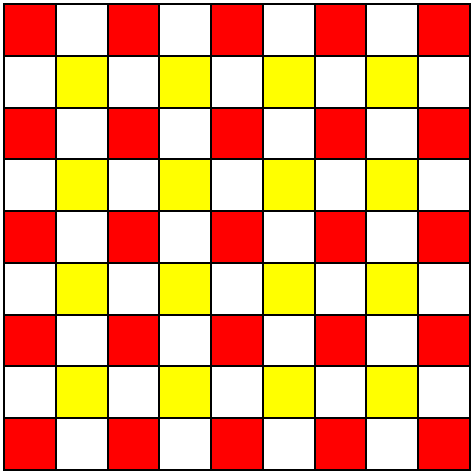
Each bug will alternate red – white – yellow – white, no matter what path it follows, because only white squares are adjacent to red ones, and going red – white – red would require continuing in the same direction for two moves.
Arsh initially focused on my groups of four squares, which I’d said I didn’t think would be useful; but in saying this he showed that he was familiar with the pigeonhole principle, as I had hoped:
Each bug needs 1 set of four adjacent squares. Even four bugs need 1 set of four adjacent squares.
This means that 65 bugs would need 17 set of 4 adjacent squares. But in 9×9 square chessboard there are just 16 set of 4 adjacent squares.
As 16 set of 4 adjacent squares can accumulate only 64 bugs, and we have 65 bugs this means that 2 bugs must be kept on same square (pigeonhole principle).
Will this proof be correct if I just elaborate it, like why 4 bugs need 1 set of 4 adjacent squares?
Unfortunately, this was the thinking that had not worked out for me; I don’t see any sense in which the 2×2 squares would be necessary. But by now, I had been able to work out a proof, more or less, so I could give more targeted hints:
You would definitely have to show that each bug “needs” four adjacent squares; but first, you’d have to clarify what that means. I wasn’t able to do that; the trouble is that a bug in fact can wander all over the board, as long as it never continues in a straight line. It can stay in one box, but that is not necessary. So I wasn’t able to turn that into a proof.
It will take something more. My mention of double-odd and double-even coordinates will be of use; I do have a solution now, which uses that as a key idea. Hint: How many squares of each type are there?
Showing that one specific method will not work (namely, putting groups of bugs into 2×2 squares) doesn’t prove that no method can work. As far as we can tell so far, the bugs might engage in some elaborate dance that takes each of them all over the board, while still following the rules.
He then read too much into my suggestion about “coordinates”:
I don’t think I would be able to prove something with coordinates. I haven’t proved anything with the coordinate geometry and have no idea how to prove.
I explained a little more:
I’m not talking about coordinate geometry, literally. I’m referring to the (integer) location of each square, taking the upper left as (1,1), then (1,2), and so on down the column. Notice that every bug will be on an (odd, odd) location and an (even, even) location once each during every 4 successive moves.
How many (even, even) squares are there? Can you arrange their locations so that on every move there are enough of those squares to hold them?
A solution
At this point, Arsh indicated that he was satisfied, though he never stated what his proof was. Let’s take a look at the details.
Have you seen it yet? The pictures may have made it easier to see than what I only said in words to Arsh.
There are 16 yellow (even, even) squares. At a given moment, 16 of the bugs can be on them. The next moment, those bugs will be on white squares, and at most 16 (different) bugs can be on yellow squares. The next moment, the first group will be on red squares, the second on white, and a new group will be on yellow — again, at most 16. The fourth moment, another group of up to 16 will be on yellow. After that, they repeat — the first group will be back on yellow, and so on.
We have just divided the bugs into four groups of at most 16 each. So there can be no more than 64 bugs, if they all remain on distinct squares. By the pigeonhole principle (or just common sense), if there are more than 64 bugs, at least one square must be occupied by more than one bug at some time.
