One of the questions we looked at in our recent survey of percent change problems involved percentages over 100%, which often confuse students. How can anything be more than 100%? Let’s look at a couple questions about that issue.
No such thing?
Take this question from 1999:
More Than 100 Percent Please help to settle an ongoing argument with a friend: is it correct to use a value of more than 100%? I say that there's no such thing as anything larger than 100%; my friend says that it is okay to say 200% or 300% and so on.
Doctor Rick replied:
There is nothing intrinsically wrong with using percentages greater than 100%. Whether this makes sense depends entirely on the context. A percentage is simply another way of writing a fraction with a denominator of 100. For example, 6% = 6/100. Just as you can have an improper fraction (a fraction whose numerator is greater than the denominator), such as 4/3, so you can have what we might call an "improper percentage" like 120% or 300%.
Since percentage is just a way to write a number, it can be used for any number. We can write 0.06 as 6% (by multiplying 0.06 by 100%), and we can write 1.2 as 120% (by multiplying 1.2 by 100%). Below, we’ll even see 1255% (that is, 12.55). In the abstract, there are no limitations.
There are situations in which a percentage greater than 100% makes no sense. For instance, "The Math Doctors answered 146% of the questions received last month." This makes no sense because if we received 5061 questions, we couldn't possibly answer more than all of them. It's just as nonsensical as saying "I ate 4/3 of the cake."
These are situations in which 100% means “all”, and there is nothing more than all.
Of course, someone could eat 4/3 of a cake – that is, 1 1/3 cakes (if they are not too large).
On the other hand, sometimes percentages are used like this: "The number of questions received was up 15.7%, from 5450 in February to 6305 in March." In other words, the increase from February to March was 6305-5450 = 855, and 855 is 15.7% of 5450. (These facts are true, by the way.)
Here, 100% doesn’t mean “all possible”, but just “all that there were in February”.
Note, by the way, that in March, 1999, Ask Dr. Math got an average of 203 questions a day. We weren’t able to answer all of them, but we did what we could. Today, there are many other places to ask questions, some of them willing to just give complete answers without making sure you could solve the problem yourself, so we get far fewer. We do answer every question that can be answered.
Now, what if the number of questions received went up to 14000 in April? (It didn't.) This would be an increase of 122% from March to April. There is nothing wrong with this - no law says that the number of questions can't do more than double from one month to the next. So the answer is, there is such a thing as a percentage larger than 100%, but not everything can have a percentage larger than 100%.
This is just one example of a place where percentages can meaningfully be greater than 100%.
More examples
A similar question came from Samantha in 2003:
Percentage as Standard for Comparison How can you have more than 100% of something? 100% indicates you have a complete item, so how can it be more than complete?
I answered this one:
Good question! In some situations, a percentage refers to a part of all there is: I can't do more than 100% of a job, or eat more than 100% of the one pizza I ordered. More than 100% of the sky can't be covered by clouds, and more than 100% of the population can't be poor.
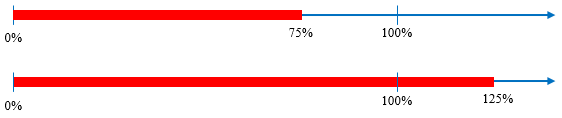
Each of these fits Samantha’s image of “a complete item”. We might picture it like this, where 100% is an entire bar; 75% is 3/4 of the bar, but 125% of it makes no sense:

But at other times, a percentage refers to something that is not an absolute limit, but just a standard for comparison. For example, the orange juice you drink in the morning may contain 100% of your daily requirement of vitamin C; if you eat any more foods containing vitamin C during the day, you will have eaten more than 100% of the RDA. For some vitamins, if you ate too much, it might be bad for you; however 130% in this case just means that you didn't need to have as much as you did, but it's okay to go beyond that. You've just taken in more than the recommended amount.
Here, 100% can be thought of as just a mark on a number line; 75% is 3/4 of the way to the mark, and 125% is 1/4 beyond the mark:
As another example, you might plan to work 10 hours to put together a project. If you keep track of the time you've used, when you have spent 6 hours on it you will have used 60% of the planned time. But you might find that you aren't quite finished when the planned time is used up. If you spend 3 extra hours to make everything just right, making a total of 13 hours of work, you will have used 130% of the planned time.
Sometimes, there is a fine line between the two cases:
Now, if there had been only 10 hours left before the project was due, you couldn't have taken 130% of that time. But you had just PLANNED to use 10 hours, and it was possible (though possibly bad for your health, or your other activities) to use extra time for the project. Just like the vitamin C requirement, 100% didn't mean "all there is," but just "all we expect." The 130% means that you are "30% over budget." Do you see the difference in these two kinds of situations? The same thing happens with fractions. I can eat 1/2 a pizza, or 2/3 of a pizza; but I can also eat 2 3/4 pizzas, because the one pizza isn't all there is. I can fill 1/2 of my stomach, or 2/3 of my stomach, but not 2 3/4 stomachs, because I only have one. Fractions can be greater than 1, and percentages can be greater than 100. It's only when the fraction or percentage refers to a part of a whole that we can't go beyond the whole.
(Of course, sometimes “whole” doesn’t mean all there is, but just a whole item of which there are more, as in the pizza example.)
Back to the nutrition label: a bag of potato chips can't be more than 100% fat, because the fat is PART of the chip, and the part can't be bigger than the whole. But it might conceivably have more than 100% of your daily requirement of fat, because the fat in the chips is only being COMPARED to the amount you're supposed to eat. Nothing prevents you from eating more. And finally, the number of calories you get from fat today can't be more than 100% of the total calories you consume, because they are part of that total. That gives us three different ways to express the fat in the chips as a percentage, and each percentage has a different meaning.
This is a key concept with both fractions and percentages: they are always relative to some “unit”. In my three examples above, the unit was (a) the total amount of fat in a chip; (b) the RDA of fat for a person; and (c) the total calories actually eaten in one day.
Here's yet another way that a percentage can be used: A copier may have a setting for enlarging or reducing what you copy. The normal setting would be 100%, meaning that what comes out is the same size as what went in. You can set it to 50%, meaning the copy will be half the size of the original. Or, you can set it to 200%, and the copy will be twice as large. There's nothing wrong with that, because the copy is not part of the original; we are only comparing it to the original. And that's what makes the difference.
Here, the unit is the original size, to which we are comparing the copy size.
There are a lot of ways percentages can be more than 100%, aren’t there?
It doesn’t look right …
Here’s one last question from 2008, illustrating the point I made last time about being fooled by large percentages:
Using Estimation to Check Your Answer What was the percent of increase in population from 1950 to 2000. In 1950 it was 38,000,000 and in 2000 it was 515,000,000. The increase was 477,000,000 but when I try to get a percentage I keep getting like 1,255%. What I find difficult is the fact that my percentage is so high and I don't think that my answer is correct and I want to find out what I might have done wrong in the problem. I've worked this particular problem about 3 times and still get the same answer and I'm so frustrated.
We recommend that students check whether an answer seems reasonable; but when your reasonableness alarm is going off because it is miscalibrated, it can lead to frustration.
I replied:
Your answer sounds reasonable to me! An increase of 1000% would mean that the increase was 10 times the original value, so with 1255% the increase would be more than 12 times the original. Since 12 times 38 is about 12 times 40, or 480, and 515 is over that, it's certainly in the right ballpark, so to speak.
I’ve changed one word from the original, where I made a small misstep in the second clause. I’m assuming that non-American readers know what “in the right ballpark” means!
Percentages this high are unusual, but that doesn't make them wrong. You just need to look at the data and see whether an unusual answer is to be expected. Since 515 million is many times 38 million, we can expect the percent increase to be huge. Knowing how to do such a "sanity check" is a good way to preserve your sanity when you're doing a problem like this!
Chanice responded:
Thank you Dr. Peterson for helping me with this problem because it was really beginning to drive me crazy. I learned new ways to look at problems and to do a "sanity check". So again I just wanted to say thanks.
If it feels wrong, it might be wrong, or you might just be misjudging it. Leaving that possibility open is helpful.

Thank you. Your article was very helpful
Thank you…because this has been driving me NUTS for YEARS!!!!
Only about 60% of your answers were helpful. On some of them, the answer wasn’t truly to the actual question asked. You changed the situation in the question and answered according to your new situation. Akin to a kid changing the rules to a game during play in order to win.
I’m not sure which 1.2 of the 3 answers here you’re complaining about, but it seems to me that if we’ve changed anything, it’s just to expand the questions and try to give a broader understanding (which I’d call a win for the student). So I’d say we answered about 130% of the questions!
A really helpful explanation, thank you.
It has driven me nuts for years —as sooo many people use this over the 100% comment. I have always taken it in the abstract form—but I loved you rationalizing of it mathematically–the Fractions comparison—super. Thank you.
At last I understand… thank you.