(A new question of the week)
Economics can be a deeply mathematical subject; but as a separate field, it has its own terminology and notation which can sometimes be confusing. Is marginal revenue (or cost, etc.) the same as the derivative of the revenue function, or is it something different? That will be the issue here.
From the archives …
We’re going to look at a question from last September about this, but I’ll start with a somewhat older question that I referred to immediately when I dealt with the new question. Here is it, from 2016:
Marginal Meanings Are 'instantaneous rate of change' and 'marginal rate of change' -- as in marginal cost -- the same thing? I ask because both of them are calculated by differentiating a function, but my experiments lead to inconsistent result. For example, let x^2 be the total cost (TC) function. I calculated a few points: x (units)----TC = f(x)-------MC 0---------------0 1---------------1-------------1 2---------------4-------------3 3---------------9-------------5 4--------------16-------------7 5--------------25-------------9 Since any unit's marginal cost (MC) is derived by differentiating the TC function, we get MC = f'(x) = 2x So we should be able to plug in the units and get the MC values above -- but instead we get f'(1) = 2 f'(2) = 4 f'(3) = 6 f'(4) = 8 f'(5) = 10 Perhaps my confusion arises because 'instantaneous rate of change' is the rate of change at a point (an instant), but we cannot measure rate of change at a point. It's the rate of change corresponding to an infinitesimally small (immeasurable) change in 'x.' BUT 'marginal rate of change' or 'marginal cost' (MC) by, definition, is the change in 'total cost' for producing one additional unit of output; and it is also derived by differentiating the 'total cost' function. Where am I making the mistake? Please explain in detail. Thank You!
Sam has calculated the marginal cost in the table as the change in the total cost, namely $$MC = TC(x) – TC(x-1)$$ and then again as $$MC = TC'(x)$$ These two calculations, both presumably based on definitions he was given, disagree. He has put his finger on the issue, which is not a mistake on his part.
I answered, with a caveat:
I am not an economist, but my understanding is that "marginal" is defined in two different ways, as you have identified. These only work out the same under certain assumptions, or as an approximation. And the two definitions may be confused somewhat.
I’ve listed three points I’ll be making: two definitions; when they agree; and use as a mere approximation.
The discrete case
First, we have to look at the basic definition, which can be stated without knowledge of calculus:
Taken literally, "the change in total cost for producing one additional unit" is TC(x + 1) - TC(x), and corresponds to the slope of a chord of the cost curve for (delta x) = 1. This definition applies specifically to indivisible, discrete items being produced, so that the smallest possible change is 1 unit. This is what I would call the DISCRETE definition of "marginal."
(Note that I’ve given a calculation a little different from Sam’s.)
This is the definition I get when I ask Google:
The cost added by producing one additional unit of a product or service.
I find the same almost everywhere I search. For Sam’s example, the total cost is represented by the red dots, and the (discrete) marginal cost by the blue vertical lines here:
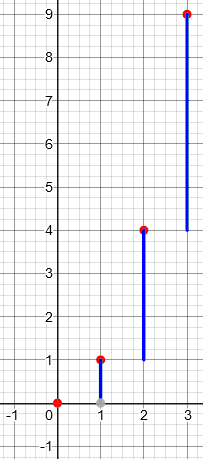
This is the amount literally added when x is increased by 1.
The continuous case
This can be approximated by the slope of a continuous curve, which is the derivative:
lim{h -> 0} [TC(x + h) - TC(x)]/h
This CONTINUOUS definition of "marginal" is applicable directly to continuous production, where the quantity can be any number at all, not just whole numbers (e.g., barrels of oil); and it can be described as the "change of total cost PER unit," which sounds much like the other definition, though it does not really mean quite the same thing.
Here the red line is the continuous function, the blue dotted line is a tangent to it, and the vertical line is the (continuous) marginal cost at x = 1:
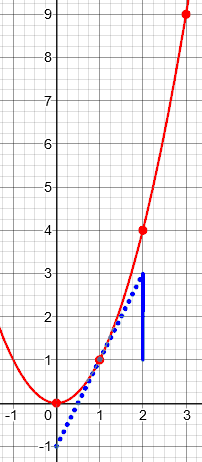
This is the instantaneous rate of change at x = 1, and represents the actual change if the rate remained the same as x increased by 1.
For comparison, we can describe speed as the distance traveled in one hour. This is not, properly speaking, the instantaneous speed; but we can take it to mean the distance you would travel in an hour IF you kept going at the same speed. Miles per hour is not taken literally as meaning the distance you traveled in the last hour ("marginal distance" in the first sense), but as the derivative of distance. If you traveled "discretely" by teleporting instantaneously once an hour, you would really have no instantaneous speed, but could calculate an average speed as the distance of one leap divided by the time between leaps.
So “discrete” marginal cost is like average speed over an hour (miles in one hour), and “continuous” marginal cost is like instantaneous speed (miles per hour at a given moment). A discrete product that can’t be produced or bought in less than a whole unit will be like the teleportation illustration, where no continuous curve actually exists.
I suspect that the derivative definition originated either as a continuous approximation of the literal, discrete definition, or as a simplification for situations in which the total number of items produced is so large that a change of 1 would be effectively infinitesimal. Or it may have been first used only for truly continuous production, and then adapted as an approximation for discrete use.
What others say
I have tried to find information about the origin of this definition, but have not been successful.
I notice that the Wikipedia article comments on this, though it reads to me like someone's private opinion that should not be there: https://en.wikipedia.org/wiki/Marginal_cost In economics, marginal cost is the change in the total cost that arises when the quantity produced is incremented by one unit; that is, it is the cost of producing one more unit of a good.... In practice, the above definition of marginal cost as the change in total cost as a result of an increase in output of one unit is inconsistent with the differential definition of marginal cost for virtually all non-linear functions. This is as the definition finds the tangent to the total cost curve at the point q, which assumes that costs increase at the same rate as they were at q. A new definition may be useful for marginal unit cost (MUC) using the current definition of the change in total cost as a result of an increase of one unit of output defined as: TC(q + 1) - TC(q) and re-defining marginal cost to be the change in total as a result of an infinitesimally small increase in q, which is consistent with its use in economic literature and can be calculated differentially.
My judgment was correct, as this content is no longer found on that page, and a search confirms that “marginal unit cost” is not a standard term. (Most of the references I find are copies of this passage!) The idea makes sense; it just isn’t used. The article currently just gives both definitions:
A conventional marginal cost is incremented by one unit; that is, it is the cost of producing one more unit of a good. …
If the cost function C is continuous and differentiable, the marginal cost MC is the first derivative of the cost function with respect to the output quantity Q: $$MC(Q)=\frac {\ dC}{\ dQ}.$$
The marginal cost can be a function of quantity if the cost function is non-linear. If the cost function is not differentiable, the marginal cost can be expressed as follows: $$MC=\frac {\Delta C}{\Delta Q},$$ where \(\Delta\) denotes an incremental change of one unit.
If this is correct, then we simply have two definitions, one for the discrete case and another for the continuous case. This makes good sense, even though it causes confusion.
A related explanation can be found in https://en.wikipedia.org/wiki/Marginal_utility#Marginality For reasons of tractability, it is often assumed in neoclassical analysis that goods and services are continuously divisible. Under this assumption, marginal concepts, including marginal utility, may be expressed in terms of differential calculus. Marginal utility can then be defined as the first derivative of total utility -- the total satisfaction obtained from consumption of a good or service -- with respect to the amount of consumption of that good or service. In practice, the smallest relevant division may be quite large. Sometimes, economic analysis concerns the marginal values associated with a change of one unit of a discrete good or service, such as a motor vehicle or a haircut. For a motor vehicle, the total number of motor vehicles produced is large enough for a continuous assumption to be reasonable. This may not be true for, say, an aircraft carrier.
(These paragraphs have not been changed, so it seems more reliable than what I copied from the other page!)
This supports my guess that the continuous definition is at least sometimes used merely for computational convenience, as a good approximation when quantities are large enough that the unit is infinitesimal by comparison.
In other words, production of goods in small quantities should be treated as discrete, because the derivative is not a good approximation; but for goods produced in large quantities, it is reasonable (and makes the work easier) to use the derivative. In your example, you had small quantities, which exaggerated the difference between the two definitions. Did you notice that your results differ only by 1, which would become insignificant for quantities in the millions?
I’ve also found this quotation from a book, Introduction to Economic Analysis by R. Preston McAfee and Don Dale (p. 12):
Marginal is just economist’s jargon for “the derivative of.” For example, marginal cost is the derivative of cost; marginal value is the derivative of value. Because introductory economics is usually taught to students who have not yet studied calculus or can’t be trusted to remember even the most basic elements of it, economists tend to avoid using derivatives and instead talk about the value of the next unit purchased, or the cost of the next unit, and describe that as the marginal value or cost. This book uses the term marginal frequently because one of the purposes of the book is to introduce the necessary jargon so that you can read more advanced texts or take more advanced classes.
This confirms my sense that the discrete definition may be particularly common simply because the concept is typically introduced to students who do not know calculus.
A second look
Now let’s look at the recent question, from Sarah:
I’m not sure if anyone can answer this question, but why is the Marginal the derivative of the total? I’m more interested in the mathematical side here. So if you have one of them, you can just find the derivative and find the other?
Also, aside from economics, if you know y is the derivative of x, and you know y, how do you find x?
I replied,
Your question reminds me of this question:
There I talk about how the derivative is sort of what marginal value means, and sort of not. That may give you an idea of the relationship and its limitations.
If you want to discuss it further, I’ll want to know the definitions you were given.
As for finding a function whose derivative is a given function, that’s called integration, and is a major topic of calculus. It’s the inverse problem to differentiation, and like many inverses, is a much harder task! There are a lot of techniques to learn, but no magic formula.
She answered:
The link you provided was an interesting read!
I define Marginal Cost as the addition in total cost brought about by the production of an additional unit.
I found another definition for MR: “MR is equal to the change in TR over the change in quantity when the change in quantity is equal to 1 unit.” This sounds more like differentiation to me.
Also, we know that TR is maximised when MR is 0. How does that work?
Now l found that when taking Total and Marginal Revenues, the maximum level of total revenue can be found through the calculation of the 2nd derivative.
I learnt these years ago, when l had no idea calculus existed. Now I’m trying to understand the mathematics behind these concepts. Seems like economics has more math than l thought!
So Sarah’s definition is the usual one, and it was taught before calculus.
I responded:
Your two definitions are equivalent, though the second is phrased so as to make it clearer that it is really a rate of change. This is the discrete definition, which is the average rate of change over a change of 1, whereas the continuous definition is the instantaneous rate of change at a point (the derivative, which is the limit of the average rate of change).
Setting the MR to zero is parallel to setting the (first) derivative to zero to find a (potential) maximum or minimum. When TR “increases” by zero, it has stopped increasing, just as when the derivative is zero. If it then starts decreasing, you have reached a maximum.
Yes, economics is a highly mathematical field. Just yesterday, one of my colleagues mentioned talking to a student who was taking two math classes, together with accounting and micro-economics, and described it as four math classes at once.
Even by the discrete definition, we can see that marginal revenue of 0 indicates a possible maximum or minimum.
The idea of two definitions for the same term can be confusing, and we went back and forth for a while on this. Sarah replied:
So how would you define MR as the derivative of TR using the discrete definition?
What about the idea of the 2nd derivative? How and when is that used?
I answered:
The discrete and continuous versions of MR are different things. Either can be used as an approximation of the other, but you can’t get the actual value of either from the other.
I’m not sure how the second derivative is used in economics. But one application is to find whether a possible extremum (max or min) is a (local) maximum or a minimum.
She said,
I wasn’t asking how to derive one knowing the other, my question was how can you define the concept of Marginal Revenue as the derivative of Total Revenue if you are defining MR discretely? – sorry if that wasn’t clear
With regard to the second derivative, l found this excellent website, in case you’re interested (or someone else asks):
http://www.columbia.edu/itc/sipa/math/calc_econ_interp_u.html
Also, what do you mean exactly when you say * local* max or min?
The page she found introduces the “marginal” concept by saying, “Let’s define this change in total cost for a given change in Q as the marginal cost.” Then it says, to students familiar with the derivative, “Therefore, taking the first derivative, or calculating the formula for the slope can determine the marginal cost for a particular good”. It then goes on to discuss second derivatives and maxima.
I answered,
I’m not sure how what you are asking is different from what I said. When you define MR discretely, you simply don’t use the derivative as part of the definition. I’m not primarily talking about “deriving”, but about “defining”; they are different, though related, concepts, so they have separate definitions. It’s because the definitions are distinct that you can’t express one in terms of the other.
Perhaps what you meant in asking, “how would you define MR as the derivative of TR using the discrete definition?” was, “how are the two definitions related?” In effect, just as the derivative is defined as the limit of average rates of change, the continuous MR is defined as the limit of discrete MR as you reduce the size of a “unit” (which would have to be explained with care).
The page you referred to uses only the continuous definition, even though it talks about “the cost of the 101st unit”, which is really inconsistent with that concept. I think they are probably just not trying to be precise about such things; the examples use small numbers of units, but in application these ideas would surely be applied to much larger numbers, where “one unit” would be tiny in context.
Even as it is in their example, the added unit is only 1% of the total so far, so it does make sense as an approximation.
As for the meaning of “local”,
A local minimum, or relative minimum as the page you referred to calls it, is the lowest point in some interval around itself: “the word relative is used to indicate a maximum or minimum point in the neighborhood of the point ( x = a)”. (“Local” means “related to a particular place”.)
For example, the cubic function y = x^3 – 3x has a local minimum at x = 1, which is not an absolute minimum because other points (not nearby) are lower.
When I teach, I try to use both terms “local” and “relative”, as both will be found when students move to other courses or find other sources online!
Sarah asked for a final confirmation:
So, just to clarify, when MR is defined discretely, is it not still the derivative of TR? I don’t quite understand the inconsistency you mention, although l agree one unit will not make much of a difference to a large firm who produces larger numbers.
I said, in conclusion,
The difference between the discrete and continuous MR is essentially the difference between average rate of change over one unit, and instantaneous rate of change. They are not the same, but are closely related, and each approximates the other.
This was good enough. But it is tricky, isn’t it?

Pingback: Derivative as Instantaneous Rate of Change – The Math Doctors