A couple recent questions offered tricks for integrating rational functions, opportunistically modifying or working around the usual method of partial fractions. We have previously discussed this method in Partial Fractions: How and Why, and in Integration: Partial Fractions and Substitution, where we looked at other variations.
First problem: A trick with negative exponents
First, a question from Amia in June:
Hi Dr math,
I want your opinion for the solution attached:
Amia started by multiplying the numerator and denominator by a negative power of x; that amounts to dividing the numerator and denominator by the greatest power in the denominator, which is a common technique for dealing with limits at infinity; perhaps that is the motivation.
Then he splits the numerator into a multiple of the denominator, plus a remainder; this amounts to long division, as we would do if the numerator had a higher degree than the denominator. The second term can then be integrated by substitution (\(u=1+x^{-2}\)).
We can rewrite the answer without negative exponents, to make it look more like we expect: $$\frac{x^{-1}}{-1}+\frac{1}{2}\ln\left|1+x^{-2}\right|=\frac{1}{2}\ln\left|\frac{x^2+1}{x^2}\right|-\frac{1}{x}+C$$
Altogether, this demonstrates what you can accomplish by “playing with possibilities” rather than following standard methods.
I answered with approval and curiosity:
Hi, Amia.
Your work looks good, and creative.
I did it more routinely, by partial fractions, and got the same result.
May I ask, what led you to think of doing that? I generally tend to change negative exponents to positive, rather than vice versa, because it’s easy to make mistakes with negatives; but I wonder if this approach could be generalized.
The routine solution
Here is the routine method using partial fractions:
$$\frac{x^2-x+1}{x^4+x^2}=\frac{x^2-x+1}{x^2(x^2+1)}=\frac{A}{x}+\frac{B}{x^2}+\frac{Cx+D}{x^2+1}\\x^2-x+1=Ax(x^2+1)+B(x^2+1)+x^2(Cx+D)\\x^2-x+1=Ax^3+Ax+Bx^2+B+Cx^3+Dx^2\\x^2-x+1=(A+C)x^3+(B+D)x^2+Ax+B$$
Equating coefficients, we get the system of equations
$$\left\{\begin{matrix}\begin{aligned}A+C&=0\\B+D&=1\\A&=-1\\B&=1\end{aligned}\end{matrix}\right.$$
From which we find that $$\left\{\begin{matrix}\begin{aligned}A&=-1\\B&=1\\C&=1\\D&=0\end{aligned}\end{matrix}\right.$$
(Below, we’ll see an example using a different approach, plugging in four values for \(x\) to obtain four equations to solve.)
So our integral becomes $$\int\left(\frac{-1}{x}+\frac{1}{x^2}+\frac{x}{x^2+1}\right)dx=-\ln|x|-\frac{1}{x}+\frac{1}{2}\ln|x^2+1|\\=\frac{1}{2}\ln\left|\frac{x^2+1}{x^2}\right|-\frac{1}{x}+C$$ just as we got above.
The inspiration
Amia replied:
The shape of this question is similar to questions I solved before
Like
1/(x^3+x)
x/(x^2+x^4)
So I tried here the same procedure, and it works.
Can we generalize this approach?
This wasn’t elaborated, but my understanding is that he is rewriting \(\frac{1}{x^3+x}\) by multiplying the numerator and denominator by x, perhaps observing that this will make a substitution (\(u=x^2\)) possible: $$\int\frac{1}{x^3+x}dx=\int\frac{x}{x^4+x^2}dx=\int\frac{\frac{1}{2}du}{u^2+u}\\=\frac{1}{2}\int\frac{du}{u(u+1)}=\frac{1}{2}\int\left(\frac{1}{u}-\frac{1}{u+1}\right)du\\=\frac{1}{2}\left(\ln|u|-\ln|u+1|\right)=\frac{1}{2}\ln\left|\frac{u}{u+1}\right|=\frac{1}{2}\ln\left|\frac{x^2}{x^2+1}\right|+C$$
We still had to use substitution and partial fractions, but the degree was reduced. Using partial fractions directly on the original integral, we would have to do this:
$$\int\frac{1}{x^3+x}dx=\int\frac{1}{x(x^2+1)}dx=\int\left(\frac{A}{x}+\frac{Bx+C}{x^2+1}\right)dx\\=\int\left(\frac{1}{x}-\frac{x}{x^2+1}\right)dx=\ln|x|-\frac{1}{2}\ln\left|x^2+1\right|=\frac{1}{2}\ln\left|\frac{x^2}{x^2+1}\right|+C$$
This doesn’t seem like a great simplification, so there may be another trick I’m missing; but the fact that a multiplication initially appears to complicate the integrand, but then makes a different approach possible, is the link between the two problems.
As for generalizing, this trick works only when it happens to work (if I’m understanding it correctly); so the generalization is just “look for possible shortcuts, rather than being locked into a routine”. That’s good advice once you’ve mastered the routines.
Second problem: Partial cancellation
Amia had another problem with another trick:
I have this solution for another question.
This integrand is another proper rational function. I’ll discuss below what he is doing, adding and subtracting \(x^2\) in order to be able to do some impressive cancelling – in both terms, not just in one as above.
For comparison, here is the work for this problem using partial fractions:
$$\frac{7x^2-16x-2}{(x^2+2)(x-2)}=\frac{Ax+B}{x^2+2}+\frac{C}{x-2}\\7x^2-16x-2=(Ax+B)(x-2)+C(x^2+2)\\7x^2-16x-2=(A+C)x^2+(-2A+B)x+(-2B+2C)$$
Equating coefficients, $$\left\{\begin{matrix}\begin{aligned}A+C&=7\\-2A+B&=-16\\-2B+2C&=-2\end{aligned}\end{matrix}\right.$$
This yields $$\left\{\begin{matrix}\begin{aligned}A&=8\\B&=0\\C&=-1\end{aligned}\end{matrix}\right.$$
So the integral becomes $$\int\left(\frac{8x}{x^2+2}-\frac{1}{x-2}\right)dx=4\ln\left|x^2+2\right|-\ln\left|x-2\right|\\=\ln\left|\frac{(x^2+1)^4}{x-2}\right|+C$$
The shortcut obtained exactly the results of the partial fractions.
Back to the first problem
I responded, applying this idea to the first problem:
I had considered mentioning a third method I had used for your problem that is essentially the idea you use in this new one, which might be called “partial cancellation”:
$$\int\frac{x^2-x+1}{x^4+x^2}dx=\int\frac{x^2-x+1}{x^2(x^2+1)}dx\\=\int\frac{(x^2+1)-x}{x^2(x^2+1)}dx=\int\left(\frac{x^2+1}{x^2(x^2+1)}-\frac{x}{x^2(x^2+1)}\right)dx\\=\int\left(\frac{1}{x^2}-\frac{x}{x^2(x^2+1)}\right)dx=\int\frac{1}{x^2}dx-\int\frac{x}{x^2(x^2+1)}dx$$
and so on.
This saves some of the work of partial fractions.
Here I saw that one of the factors of the denominator is found in the numerator, so that splitting the fraction in that way permitted cancellation in each of the resulting fractions.
Let’s finish the work, avoiding the temptation to cancel in the second fraction, and instead taking advantage of an opportunity for substitution (\(u=x^2\)), just as I did in what I called “the inspiration” above:
$$\int\frac{1}{x^2}dx-\int\frac{x}{x^2(x^2+1)}dx=\int x^{-2}dx-\frac{1}{2}\int\frac{du}{u(u+1)}\\=-x^{-1}-\frac{1}{2}\int\left (\frac{1}{u}-\frac{1}{u+1}\right)du=-\frac{1}{x}-\frac{1}{2}\left(\ln\left|u\right|-\ln\left|u+1\right|\right)\\=-\frac{1}{x}-\frac{1}{2}\ln\left|\frac{u}{u+1}\right|=-\frac{1}{x}-\frac{1}{2}\ln\left|\frac{x^2}{x^2+1}\right|=\frac{1}{2}\ln\left|\frac{x^2+1}{x^2}\right|-\frac{1}{x}$$
The aspect of your original solution that caught my attention was the use of negative exponents, which seems highly unusual; but this aspect, breaking the numerator into two parts that can be canceled separately, is also present, and can definitely be used for many problems.
In your work this time, you’ve taken that idea one step further, using a technique I’ve seen used in factoring (e.g. Factoring Tricks from an Old Textbook).
In general, integration is an art, and setting yourself free to consider non-standard options when you see they might be useful is a valuable skill. Both aspects of your solution are potentially useful.
In the page referred to, I called this trick “wishful thinking” (in problems A and D), adding and subtracting a term (\(x^2\) for Amia) that put one part into a desirable form:
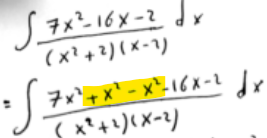
Third problem: alternative numerator for squared linear denominator
Back in March of last year, Amia had a similar question, this time not evading partial fractions, but trying an alternative detail:
Hi Dr math,
I have a question about integration by partial fractions.
The question is attached:
Here he is using partial fractions, but chooses to take a linear numerator for the term with denominator \((x-1)^2\), rather than split it into two terms, one with denominator \((x-1)\), and the other \((x-1)^2\), as we traditionally do. We mentioned this possibility (and showed why it is not preferred) in Partial Fractions: How and Why; the example there has denominator \((x-2)^3\) and we consider using \(Bx^2+Cx+D\) as the numerator, but point out that that is not useful for integration. Here Amia is demonstrating that it can be done, and what happens when you do it, which will add to what we said there.
He uses the alternative method for solving for A, B, and C that I mentioned above. When it comes to integrating this term, he uses the “partial cancelling” method we saw above, splitting it again into two fractions (which, as we’ll see, are the same as we’d get the other way).
Unfortunately, he makes a small error or two, so I’ll redo his work in order to have a correct answer to compare:
$$\frac{3x^2+2}{x(x-1)^2}=\frac{A}{x}+\frac{Bx+C}{(x-1)^2}\\3x^2+2=A(x-1)^2+(Bx+C)x$$
Setting x to 1, 0, and 2 as he did, we get $$\left\{\begin{matrix}\begin{aligned}&x=1:5=B+C\\&x=0:2=A\\&x=2:14=A+4B+2C\end{aligned}\end{matrix}\right.$$
Solving for the constants, $$\left\{\begin{matrix}\begin{aligned}&A=2\\&B=1\\&C=4\end{aligned}\end{matrix}\right.\\$$
so that the new form is $$\frac{3x^2+2}{x(x-1)^2}=\frac{2}{x}+\frac{x+4}{(x-1)^2}$$
(You can check that this is true.)
Now we integrate, using Amia’s trick:
$$\int\frac{3x^2+2}{x(x-1)^2}dx=\int\frac{2}{x}dx+\int\frac{x+4}{(x-1)^2}dx\\=\int\frac{2}{x}dx+\int\frac{(x-1)+5}{(x-1)^2}dx\\=\int\frac{2}{x}dx+\int\frac{1}{x-1}dx+\int\frac{5}{(x-1)^2}dx\\=2\ln|x|+\ln|x-1|-\frac{5}{x-1}\\=2\ln\left|\frac{x}{x-1}\right|-\frac{5}{x-1}+C$$
We’ll compare this to the standard method below.
Why the result is the same
Doctor Fenton answered, showing that the process is equivalent:
Hi Amia,
Yes, that is valid, but you are not really doing anything differently. Note that
$$\frac{Bx+C}{(x-1)^2}=\frac{B(x-1+1)+C}{(x-1)^2}=\frac{B(x-1)+B+C}{(x-1)^2}\\=\frac{B}{x-1}+\frac{B+C}{(x-1)^2}=\frac{B}{x-1}+\frac{D}{(x-1)^2}$$
where D = B + C.
Instead of solving for B and D, you solve for B and the sum B + C, from which you can determine D.
This shows that his work produces the same form as the usual partial fractions method. Let’s actually do the latter and see that we get the same fractions:
$$\frac{3x^2+2}{x(x-1)^2}=\frac{A}{x}+\frac{B}{(x-1)}+\frac{C}{(x-1)^2}\\
3x^2+2=A(x-1)^2+Bx(x-1)+Cx\\
3x^2+2=Ax^2-2Ax+A+Bx^2-Bx+Cx\\
3x^2+2=(A+B)x^2+(-2A-B+C)x^2+A$$
Equating coefficients, we get the system of equations
$$\left\{\begin{matrix}A+B=3\\-2A-B+C=0\\A=2\end{matrix}\right.$$
From which we find that $$\left\{\begin{matrix}A=2\\B=1\\C=5\end{matrix}\right.$$
This gives the fractions $$\frac{2}{x}+\frac{1}{(x-1)}+\frac{5}{(x-1)^2}$$
Integrating, we get
$$\int\frac{2}{x}dx+\int\frac{1}{x-1}dx+\int\frac{5}{(x-1)^2}dx\\=2\ln|x|+\ln|x-1|-\frac{5}{x-1}\\=2\ln\left|\frac{x}{x-1}\right|-\frac{5}{x-1}+C$$
just as we did above.
Amia replied:
Thank you Dr,
But I see it is easier when we do the integrations:
A/(x-1), B/(x-1)². ??
I’m right?
Doctor Fenton responded:
Yes. When you integrate
(Bx + C)/(x – 1)2 ,
unless C = -B, in which case it becomes B(x – 1)/(x – 1)2 = B/(x – 1), then you will have to break up the integrand in the same way.
As we said in the older page, “Our motivation for partial fractions is their use in calculus, and that drives the required form of the fractions. What I suggested above would otherwise be perfectly valid, and we would not need all the specific rules that are taught. But then the calculus would be harder. (I will not go into the details, but you might like to try integrating an expression of the form above, to see why.)”
So despite the fact that we can sometimes use special tricks to simplify part of the work, on the whole, the method of partial fractions has been refined over the years to a nearly-optimal method.

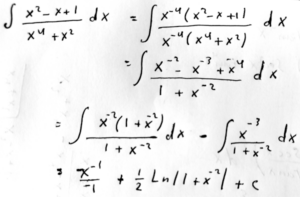
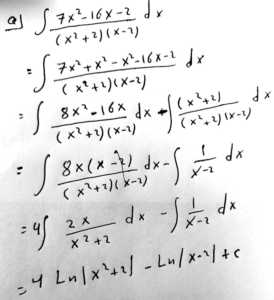
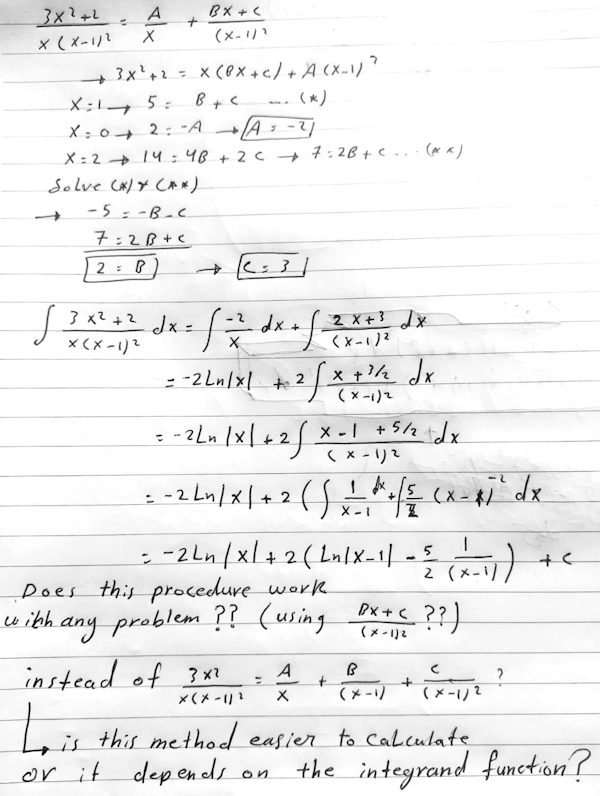
Pingback: Sign Issues in Integration – The Math Doctors