Fractions: What Are They, and Why?

We’ve looked at some specific ideas about fractions (their proper definition, their relationship to decimals, and how to divide them); it’s time to go through this topic from the beginning. Here we’ll look at how they are introduced to beginners, and how to keep them from hurting our brains!

Parts of a whole

Although, as we saw in What is a Fraction, Really?, the mature view of a fraction is a representation of a number, or “a division that hasn’t been done yet”, we tend to introduce them concretely, as parts of a whole, commonly of a “pie”. The following question, from 2001, gave us a chance to start with the basics:

Draw Three Parts and Shade Two

I've been having problems understanding fractions and being embarrassed when I go to the board and draw three parts and shade two in, and have to tell the teacher the name of the fraction I've shaded. Can you help me?

I’ve seen students, even those who are studying calculus, who struggle with fractions! Here we are catching a student (who chose to be anonymous) at the beginning, and perhaps in time to minimize future difficulties. I answered:

I'll give you a basic introduction to the idea of fractions. If you need more help, I hope you won't be embarrassed to show me your mistakes, so I can help you figure out what you are doing wrong and learn how to do it. You can probably also ask your teacher for some private help, so you don't have to make your mistakes in front of the class.

We didn’t get a reply, but I hope this advice helped ease the stigma.

A fraction is just a way to say "I've broken something into some number of pieces, and chosen some of them." It has two parts:

     2  <--- the numerator
    ---
     3  <--- the denominator

The numerator is the "numberer" (that's what the word means in Latin). It tells how many pieces I've chosen.

The denominator is the "namer" (again, it's Latin). It tells what kind of pieces they are.

For a little more on the origin of these terms, see

Numerator, Denominator: Etymologies

The important thing here is the meaning of the words. The top number is how many pieces we have, and the bottom number names the pieces in terms of how many make up a whole, which tells us their size. Our example, 2/3, means “2 of 3 equal parts”; each part is a “third” (its name).

You make the pieces by cutting a whole into some number of parts. If you cut it into three parts, we call them thirds, and write "3" for the denominator. For most numbers, the word we use for the denominator is the same as the word we would use to say the order of things: first, second, third, fourth, fifth, and so on. In a few cases, though, we use special words. A "first" (only one part) is just called "the whole"; you haven't cut it at all if you've cut it into one piece. A "second" is called a "half"; cutting it in two means cutting it in half. A "fourth" can be called that, but is also often called a "quarter" (like the coin, which is a fourth of a dollar). Otherwise, we use the usual words.

This part is not so much math as English! In any language, the words for small numbers don’t follow the patterns that larger numbers follow, so you just have to learn them: whole, half, third, quarter, fifth, …. It can be easy to overlook this matter of language when introducing the idea of fractions.

So if you cut a pie into three equal parts and color in two of them, the fraction you have colored in is 2/3, or "two thirds." Each piece is a third, and you colored two of them.

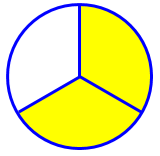
It’s important to keep in mind that we are not just naming pictures; we are creating numbers representing how many circles we have. The number we just made, \(\frac{2}{3}\), is a number less than 1, representing part of a whole. (One circle here is called a unit, represented by the number 1.)

If you cut each of a batch of pies into one piece each (that is, you leave them whole), and take five of them, you've taken 5/1, which we can just call five pies, since there are five pieces, each of them a whole pie.

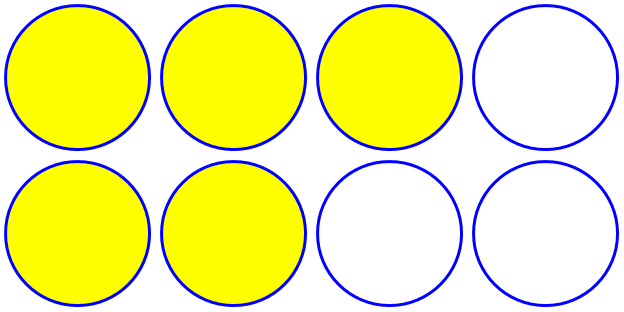
This picture could also be used to represent the fraction \(\frac{5}{8}\), if we said that the “unit” was all 8 circles. I am taking the unit to be one circle, throughout. So this picture is how we would represent the whole number 5.

We could also have a mixed number in which we take some whole circles and some parts. The following represents the number \(2 \frac{3}{4}\):

Equal parts?

Here is another question, from 2003, clarifying a detail of this picture:

Do Fractions Have to be Equal?

My grandson's textbook defines fractions as "one or more of the equal parts of a whole." Is this true? Do the parts of the whole have to be equal?

Phil may have one of several uncertainties here, and a couple of us took a stab at it. I answered first:

The book is correct, though there can be some misunderstandings about what it is saying.

When we name a fraction such as 1/3, we mean that you COULD obtain this amount by cutting three EQUAL pieces and taking one of them. We don't necessarily mean that you DID cut it just that way. But we do mean that if you cut a pie into three DIFFERENT pieces, they can't all be called thirds.

Here is a pie cut into thirds (as well as I can do so in text!):

                      ooooooooo
                oooooo.........oooooo
             ooo.................../ ooo
           oo...................../     oo
         oo....................../        oo
        o......................./           o
       o......................./             o
      o......................./               o
     o......................./                 o
     o....................../                  o
    o....................../                    o
    o---------------------.                     o
    o                      \                    o
     o                      \                  o
     o                       \                 o
      o                       \               o
       o                       \             o
        o                       \           o
         oo                      \        oo
           oo                     \     oo
             ooo                   \ ooo
                oooooo         oooooo
                      ooooooooo

All three pieces are equal, and I have chosen one of them, so that piece is 1/3 of the pie.

This is the classic image of \(\frac{1}{3}\); but it is not the only such picture we could make.

Here is a pie cut into three pieces that are not equal, but the chosen piece is still 1/3, because I COULD have made it the same way as before:

                      ooooooooo
                oooooo.........oooooo
             ooo.................../ ooo
           oo...................../     oo
         oo....................../        oo
        o......................./           o
       o......................./             o
      o......................./               o
     o......................./                 o
     o....................../                  o
    o....................../                    o
    o---------------------+---------------------o
    o                                           o
     o                                         o
     o                                         o
      o                                       o
       o                                     o
        o                                   o
         oo                               oo
           oo                           oo
             ooo                     ooo
                oooooo         oooooo
                      ooooooooo

Only the shaded piece is actually 1/3; the others happen to be 1/6 and 1/2. Because they are not equal, we can't call them thirds. But the shaded piece is the same size as the third I made before, so it can be called 1/3.

This illustrates my statement that what matters is not how it was made (in this case, by cutting into three non-equal pieces) but how it could have been made (or the fact that a circle could be made from it).

Saying the same thing without pictures: If we multiply \(\frac{1}{3}\) by 3 (that is, make 3 identical pieces), then together they will make 1. If not, then it isn’t \(\frac{1}{3}\).

Here is another pie, which I cut into six pieces, but I chose two of them; the shaded area is still 1/3, because again I could have cut it into three equal pieces to get the same amount:

                      ooooooooo
                oooooo.........oooooo
             ooo.\................./ ooo
           oo.....\.............../     oo
         oo........\............./        oo
        o...........\.........../           o
       o.............\........./             o
      o...............\......./               o
     o.................\...../                 o
     o..................\.../                  o
    o....................\./                    o
    o---------------------+---------------------o
    o                    / \                    o
     o                  /   \                  o
     o                 /     \                 o
      o               /       \               o
       o             /         \             o
        o           /           \           o
         oo        /             \        oo
           oo     /               \     oo
             ooo /                 \ ooo
                oooooo         oooooo
                      ooooooooo

(Of course, this can also be called 2/6, which is equivalent to 1/3.)

This illustrates both the fact that you don’t have to have cut it into only three pieces, and the concept of equivalent fractions (that is, different names for the same quantity). We’ll be getting there next week.

And here is a pie that I cut into three unequal pieces, none of which is a third:

                      ooooooooo
                oooooo....|    oooooo
             ooo..........|          ooo
           oo.............|             oo
         oo...............|               oo
        o.................|                 o
       o..................|                  o
      o...................|                   o
     o....................|                    o
     o....................|                    o
    o.....................|                     o
    o---------------------*                     o
    o                      \                    o
     o                     \                   o
     o                      \                  o
      o                     \                 o
       o                     \               o
        o                    \              o
         oo                   \           oo
           oo                 \         oo
             ooo               \     ooo
                oooooo         oooooo
                      ooooooooo

The point is that a third is not defined based on how you make it, but based on how big it is. If three identical pieces put together make up a whole, then those pieces are thirds. Three different pieces, or three pieces that don't add up to a whole, are not necessarily thirds.

Again, a fraction is not an object, but a name for a quantity.

In informal usage, words get a lot fuzzier:

Note also that this defines "fraction" in this specific mathematical sense. In everyday language we can use the word in other ways, such as "only a fraction of the population understands math well." We can even talk about one child getting the "bigger half" of a pie. But when we are writing a fraction using a numerator and denominator, the denominator has to indicate a number of equal pieces into which a whole can be cut, and the numerator is the number of those pieces chosen.

Does that help to clarify things?

Doctor Dotty also answered. After giving an example similar to mine, she said:

The definition was slightly confusing though, I agree, as it could be taken (as I suspect you did) as meaning that all fractions regarding the same whole have to have the same denominator - rather than you can't have two different denominators in the same fraction.

A better way of defining a fraction could be:

"A number written in the form a/b where both a and b are integers."

Does that make sense?

This final definition is the true mathematical definition, which has nothing to do with pies. It is not, of course, a full definition, as it says nothing about what \(\frac{a}{b}\) actually means! A mathematician’s definition would include what it means for two fractions to be equivalent (that is, to represent the same quantity), and how operations are done on them; and those formal definitions are based on the informal concepts that are introduced with pies. There is plenty of time to make that leap from the concrete to the abstract.

Why do we have fractions?

A 2007 question asks something that many kids probably have in the back of their minds:

Why Were Fractions Invented?

Why were fractions invented?

No, Dominique, they were not invented just to torment kids. I replied:

Hi, Dominique.

Fractions were invented to provide a way to work with quantities smaller than one, such as 2/3 (or quantities between two other whole numbers, such as 3 2/3).  If we had only whole numbers, then the only way to talk about such quantities would be to use a smaller unit.  In fact, that's essentially what the Romans did (who weren't very good mathematicians in general).  They could talk only about whole numbers of feet; when they wanted to work with parts of feet, they would change to inches (of which there were, and are, 12 in each foot). Then what we might call 1/12 foot would be called 1 inch, using a whole number; 1/4 foot would be called 3 inches.  (Our word "inch" comes from their word "uncia", which meant 1/12 of anything--the smaller unit).

Since they had no effective way to say “\(\frac{1}{4}\) foot”, they had to use inches to describe such a length, namely “3 inches”; and they had to call \(\frac{3}{4}\) foot “9 inches”. That’s not hard; in fact, we usually avoid fractions just that way, by using small enough units that we can use whole numbers – when possible! The trouble is, it isn’t always possible.

But what if your measurement isn't even a whole number of inches? Then you'd need a still smaller unit to measure it.  If you want to be very precise, things get more and more complicated.

Fractions are sort of do-it-yourself units.  You decide what size unit you need in order to measure something, by choosing how many of them there will be in each of the existing unit; say you want 8 units per foot.  Then the new unit is called an eighth, and rather than writing its name we just call it 1/8.  Now we can measure any number of eighths; 3 of them is written as 3/8.  The numerator tells how many of the unit you have, and the denominator tells what the unit is.  (The word "numerator" is Latin for "numberer"--how many; the word "denominator" is Latin for "namer"--what kind of unit.)

You see, to talk about eighths, the Romans would have to invent a unit smaller than an inch (maybe an “unciuncia” for a 12th of an inch?); but an eighth of an inch wouldn’t even be a whole number of those, so they’d be stuck. We need a temporary unit that we can use just for this problem. And that’s exactly what fractions give us. When we need eight parts, we make a new unit called an “eighth”. And rather than have to make up a special word for this unit, we just write the denominator (the name of the unit) under the numerator (the number of those units), and we have everything we need: \(\frac{3}{8}\) means 3 of these things called eighths.

This makes it possible to measure all sorts of things without having to name lots of new units.  Moreover, by having a nice way to write them, we can add, subtract, multiply, and divide any fractions easily (compared to what the Romans would have had to do, if they even bothered to try).  And that's the benefit of fractions.

That’s why; how about when?

This kind of fraction was invented hundreds of years after the end of the Roman empire, by Hindu mathematicians, and our notation (using the fraction bar) was established by Arabic mathematicians.

(It can be tricky identifying the peoples involved in math history; I said “Hindu” here as if it were their religion that mattered, and “Arabic” as if they were ethnic Arabs, though in fact some were Persians or other groups (and they were not necessarily Muslim either). But these were people within broadly defined cultures associated to some extent with these terms. Better terms might be Indian and Arabic/Islamic, respectively. See the footnote at the bottom of this post.)

There are other solutions to the same problem.  The decimals we use (which you may or may not have learned about yet) were invented by the Arabs, and got their current form around 1500 in Europe.  But the ancient Babylonians had a very similar idea, based on 60 rather than 10, which was used by ancient astronomers--and is still the basis of our degree measurement of angles, as well as minutes and seconds of time.

Decimals amount to a fixed set of new units (compare the metric system) in which only tenths are used; the rigidity helps keep things consistent, but sometimes prevents precision. More on that next time!

Broken pieces

I’ll close with this 2002 question:

The Joy of Fractions

How come fractions are called fractions?

How come they can be translated into decimals?

Why do they hurt your brain when you first learn them?

Doctor Ian replied:

Hi Nicole,

The word 'fracture' means to break into pieces, and 'fraction' comes from the same root.  When you break something into pieces, each piece is a 'fraction' of the whole.

The reason a fraction can be translated into a decimal is that a fraction is really just a division that you haven't done yet.  So when you see something like 3/4, it's just a way of saying "the number that you'd get when you divide 3 by 4".  That is, 3/4 is just another name for 0.75, which is just another name for 75/100, and so on.

And, thinking back on our pie model, dividing a pie by 4 breaks it up into four equal pieces; the fraction \(\frac{3}{4}\) tells one way to make this smaller-than-one quantity, just as the division \(12\div 4\) tells you one way to get the number we call 3. Both notations describe, rather than do, the division they identify.

Why would you want to have such a notation?  Well, in many cases it turns out that you would divide by something now only to end up multiplying by the same thing later.  By putting off doing the multiplications and divisions, you can sometimes avoid doing them.  (This is one of the few times in life that procrastination can actually pay off.)

This is followed by an example of simplifying, which is beyond my subject here. In general, it turns out that postponing operations can save a lot of work. And that is what a fraction is: a postponed operation.

As for making your brain hurt, maybe you can learn to think of that feeling the way that body builders learn to think of muscle soreness: as a sign of growth.  When a body builder lifts a lot of weights, his muscles hurt the next day, but that's partly because they're growing, so the next time he tries to lift the same weights, it will be easier.  Maybe it's the same thing with brains?

A nice, positive perspective on learning!

Footnote: Consider this quotation from the article Arabic mathematics : forgotten brilliance?:

Before we proceed it is worth trying to define the period that this article covers and give an overall description to cover the mathematicians who contributed. The period we cover is easy to describe: it stretches from the end of the eighth century to about the middle of the fifteenth century. Giving a description to cover the mathematicians who contributed, however, is much harder. The works [6] and [17] are on “Islamic mathematics”, similar to [1] which uses the title the “Muslim contribution to mathematics”. Other authors try the description “Arabic mathematics”, see for example [10] and [11]. However, certainly not all the mathematicians we wish to include were Muslims; some were Jews, some Christians, some of other faiths. Nor were all these mathematicians Arabs, but for convenience we will call our topic “Arab mathematics”.

Humans are so much harder to define than numbers!