Diluting a Solution: Math vs. Reality

Here is a little question about making a formula to dilute a solution; we’ll see how to do the algebra, and also how what we teach in math classes isn’t quite real.

Finding a formula

The question is from Conor, in early March:

Is there a formula to determine the amount of liquid needed for dilution?

For example, say I have 500 ml of 75% ABV (150 proof) alcohol and need to add water to dilute it to 35% ABV (70 proof), is there a simple formula where I can just plug in the numbers to determine how much I should add?

“ABV” means “alcohol by volume”, and “proof” means twice that number (for interesting historical reasons, based on how it was tested).

We would often ask a “patient” to show what they have tried, so we can get a sense of what sort of help they need; but Conor indicated that he was neither a student, teacher, or parent, but “other” – someone who just needs to use the math. So Doctor Rick gave a direct answer, teaching the “how” without withholding details for pedagogical reasons:

Hi, Conor, thanks for writing to the Math Doctors.

I will first show you how we can use a little math to create our own simple formula. Then I will explain why this simple formula is not really accurate, and an accurate formula would not be simple!

Sounds like a plan!

The particular example

Let’s start with your example numbers and their meaning:

For example, say I have 500 ml of 75% ABV (150 proof) alcohol and need to add water to dilute it to 35% ABV (70 proof).

You have a total of 500 ml of an alcohol-water mixture. It is 75% alcohol by volume, so the amount of alcohol in the mixture is

0.75 × 500 ml = 375 ml.

You want to add more water so that this alcohol (375 ml) so that the new mixture is 35% alcohol by volume.

Here is a picture, with red representing alcohol, and yellow representing water:

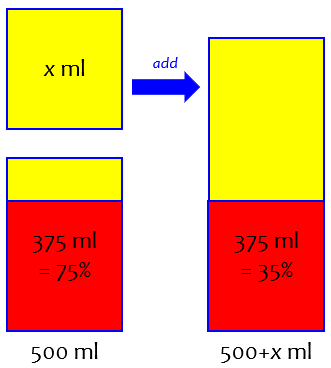
I’ll use a little algebra, which requires that I give a name to the unknown amount of water: let’s say I will add x ml of water. Then the total volume is (500 + x) ml, but the volume of alcohol is still 375 ml. I calculate the fraction of the new mixture that is alcohol, by dividing the volume of alcohol by the total volume; I want the result to be 35%, or 0.35:

375/(500 + x) = 0.35

This is how algebra is typically applied: We write an equation that represents the goal, and then we use algebra to solve it. We’ve seen how to calculate the percentage of alcohol if we knew that unknown amount of water; then algebra unwinds the calculation to find what the unknown has to be.

To solve this equation for x, I first multiply both sides of the equation by (500 + x):

375 = 0.35 × (500 + x)

Apply the distributive property to the right-hand side:

375 = 0.35 × 500 + 0.35 × x

375 = 175 + 0.35x

Subtract 175 from each side:

200 = 0.35x

Finally, I divide both sides by 0.35, which leaves x alone on one side; the other side is the value of x that makes the original equation true:

x = 200/0.35

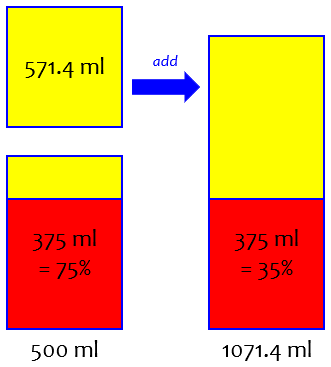
x = 571.4

So you need to add about 571.4 ml of water to get 35% ABV.

We had to round the answer, which otherwise would have been 571.42857…!

Here is the solution:

This is the sort of algebra students generally learn first.

Let’s check that answer: after adding that volume of water, the total volume of the mixture is 1071.4 ml, of which 375 ml is alcohol. We calculate the percentage of alcohol:

375 / 1071.4 = 0.35 = 35%

It worked!

Or we could just check that 35% of 1071.4 is 375: \(0.35\times1071.4=374.99\), showing that the answer is not exact, but as close as we can get, rounded.

I recommend doing this sort of check whenever you care about getting the right answer. We worked backward to find the answer; now we work forward (which is more natural, and therefore more likely to be done correctly) to see if it works.

A general formula

Now, I will make this into a general formula. To do that, I replace the numbers 500 ml, 75%, and 35% with the variables V_i (the initial total volume of mixture), P_i (initial percentage ABV), and P_f (final percentage ABV). If I do all the same things I did with the numbers above, I will get the equation

P_iV_i / (V_i + x) = P_f

whose solution is

x = V_i (P_i – P_f ) / P_f

This formula can also be written as

x = V_i (P_i / P_f – 1)

Having done the work of solving with numbers, as sort of a dry run, we just have to do the same things with letters (which generally feels a lot less natural). Here is what the work looks like in this form:

$$\frac{P_iV_1}{V_i+x}=P_f$$ $$P_f(V_i+x)=P_iV_i$$ $$P_fV_i+P_fx=P_iV_i$$ $$P_fx=P_iV_i-P_fV_i$$ $$P_fx=V_i(P_i-P_f)$$ $$x=\frac{V_i(P_i-P_f)}{P_f}=V_i\left(\frac{P_i}{P_f}-1\right)$$

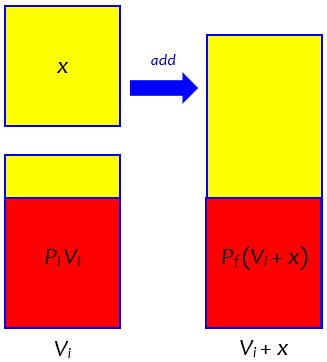
One more check to see that this works with your example: replacing V_i with 500, P_i with 75, and P_f with 35, I find

x = 500(75/35 – 1) = 571.4

Good, it worked!

This confirms that the algebra we did with the general formula agrees with the initial work for the specific example.

Reality creeps in

Now for the bad news, though it may not be too bad. I made a simplifying assumption in the work above: that when you add two volumes of different mixtures (500 ml of 75% ABV and 571.4 ml of pure water, for instance), the volume of the resulting mixture will be the sum of the volumes I started with. I know this assumption is not always true, so I checked online, and Wikipedia had this to say:

Mixing two solutions of alcohol of different strengths usually causes a change in volume. Mixing pure water with a solution less than 24% by mass causes a slight increase in total volume, whereas the mixing of two solutions above 24% causes a decrease in volume…. Thus, ABV is not the same as volume fraction expressed as a percentage … defined as the volume of a particular component divided by the sum of all components in the mixture when they are measured separately.

This is a point I commonly make when teaching about this sort of problem in an algebra class: The textbooks typically make the assumption that volume is conserved without stating that it is only an assumption, and is false for many liquids. I tell students to make the assumption the book uses, but not to do the same in a chemistry class!

My work above assumed that ABV is the same as the volume fraction; notice that I added the volume x to the initial volume, assuming that would be the new volume. Now we see that my formula is not accurate. However, the article goes on to say:

The difference is not large, with the maximum difference being less than 2.5%, and less than 0.5% difference for concentrations under 20%.

So if you are OK with your result being off by as much as a few percent, you can live with the formula I showed you above. If not, it will take more work involving empirical data, such as the graph of “excess volume” shown in the Wikipedia article. You may be able to find a more accurate formula somewhere online, but it’s beyond the realm of pure math.

Here is the graph from the article:

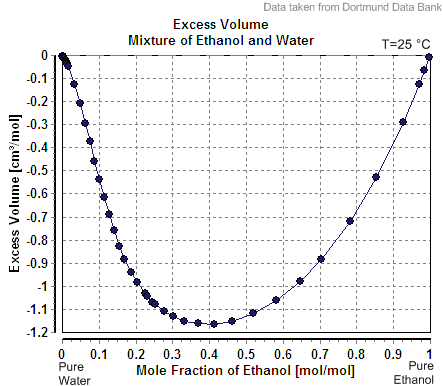
To use this, it appears that we would need to convert our ABV to moles of alcohol per mole of mixture, and use the appropriate number from the graph to adjust the volume of mixture in our formula. I would also want to check my work against the statements about concentrations above and below 24%.