Different Ways to Solve a Probability Problem

Sometimes there are several ways a problem could be solved, and we encourage students to pursue the path they’ve started on, rather than give them a method that may not be natural to them. (And we encourage them to start, if they haven’t yet, in part so we can see what might be most helpful to them.) I sometimes tell students, “The best way to solve a problem is the way you see.” Here, we’ll look at a probability problem about children randomly standing in a line, and two ways to solve it – one good, the other surprisingly fast.

Five kids between them …

The question came in early November from Thulani (a non-math teacher, apparently from South Africa):

Ten learners stand randomly in a line, one behind the other.

Calculate the probability that there will be 5 learners between the 2 youngest learners in the line.

I presume “learners” here means what I would call students.

Doctor Rick answered with the first step: pondering the exact meaning of the problem.

Hi, Thulani.

There is a little ambiguity here: is it saying there are exactly five, or at least five, learners between the two youngest? Either interpretation is possible; if the two youngest (let’s call them A and B) are in positions 3 and 10, then there are five learners between them — and another learner as well. I think most likely “exactly five” is meant, but my answer would start by stating this assumption.

What I just said contains some starting ideas for solving the problem. Can you show me your own thoughts? If students are getting more than one answer, can you tell me what they are saying?

When I help a student with a somewhat ambiguous problem, I often give the same advice, to state your interpretation before showing your work. Even better, if possible, you should ask the teacher what meaning was intended. If you were solving the problem for your boss or a customer, it would be embarrassing to do pages of work and then find that you had answered the wrong question. They would ask, “Why didn’t you ask me for clarification?”

Here is his example with more than five, supposing that the students, in increasing order of age, are A, B, C, D, E, F, G, H, I, and J:

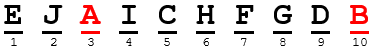
This is presumably not what the problem intends; but it is a possible interpretation, and in some problems “at least five” would be reasonable, as illustrated in Should Rare Events Surprise Us?. Here, one might, for example, want to make sure these two children always have at least five children between them, because otherwise they would get in trouble; the teacher might ask, “Are there five kids between Andy and Ben?” The answer would be, yes! But that’s unlikely to be the intent of this problem … I think.

Here is an example of the case we will actually be counting:

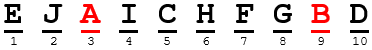
And here’s another, where B is in front:

Listing a couple examples like these can be a big help in getting started toward a solution. Including examples can also help clarify the meaning of a problem you write.

A near solution

Thulani showed a good attempt:

Position 3 and 10 confuses me.

I was thinking of treating 7 (first youngest – 5 learners – second youngest) learners as a unit. Then I would consider 4 spots. which will be (4!* 2! * 5!) / 10!

The idea here, which is excellent, is to treat the line of ten as 4 items (three individuals and one group) that can be arranged in any order:

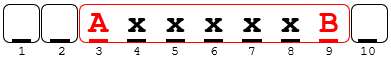
There are \(4!\) ways to arrange these four items, \(2!\) ways to order A and B, and \(5!\) ways to arrange 5 students in the middle. The denominator is the total number of ways to arrange all 10 students. Thulani’s answer is $$\frac{4!2!5!}{10!}=\frac{4\cdot3\cdot2\cdot2}{10\cdot9\cdot8\cdot7\cdot6}=\frac{1}{10\cdot9\cdot7}=\frac{1}{630}.$$

There’s just one thing wrong …

Doctor Rick replied:

(When I mentioned the pair (3, 10), that was under the supposition that we wanted at least five learners between A and B; in that example, six.)

I believe you’re saying that there are 4! ways to arrange the group of 7 and the other three learners. Then your 2! * 5! comes from permuting the two youngest (whom I called A and B) in the two outer positions of the group, and permuting the five in the middle.

Have you forgotten about choosing which five are in the group (between the two youngest)? I think that should give you a correct solution.

Once the five on the inside are chosen, the other three are known, so they don’t have to be chosen separately.

A quicker way

On the other hand, there are always more ways than one to work these out:

I had a solution in mind that, to me, is a bit of a shortcut. I start by considering that the two youngest, A and B, must be in one of four pairs of positions: (1, 7), (2, 8), (3, 9), or (4, 10).

Here are the four possible pairs (apart from reversing A and B):

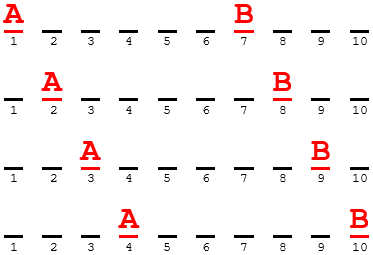
We’ll come back to this.

Finishing the first way

Thulani responded:

Thanks for response. Now it’s even more interesting. You made me aware of choosing which five are between the youngest. Will think about this. Is it kind of a combination of 8 learners taking 5 at the time? Please note I’m not strong at this topic.

Doctor Rick had more questions:

That’s correct. To find the number of ways that five learners could be chosen to be between the two youngest, you use C(8, 5). Alternatively, you could choose the three learners who are not between the two youngest; you’ll get the same result, since C(8, 3) = C(8, 5).

What is your final answer — the probability as a reduced fraction?

Then I can show you my alternative solution (which gives the same answer, of course).

Instead of using combinations as indicated, we could instead have replaced \(5!\), which counted ways to permute 5 already-chosen students, with \(_8\text{P}_5=\frac{8!}{(8-5)!}=8\cdot7\cdot6\), the number of ways to choose and permute some 5 of the 8 students. Then the result would be $$\frac{4!2!_8\text{P}_5}{10!}=\frac{4!2!8!}{3!10!}=\frac{4\cdot3\cdot2\cdot2\cdot8\cdot7\cdot6\cdot5\cdot4}{10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}=\frac{4}{5\cdot9}=\frac{4}{45}.$$

He added,

You say you are a teacher. Do you need to teach on probability and combinatorics? Is this specific problem one that is assigned to your students? (Now and then someone will say his/her role is “teacher” but they do not teach math, so I just want to check.)

Thulani replied:

I’m teaching mainly IT. Wanted to create an app to help with the counting principle so I needed data to test it.

So correct answer would be:

(4!* 2! * 5!*8!) / (10!*5!*3!) ?

This is $$\frac{4!2!5!_8\text{C}_5}{10!}=\frac{4!2!5!}{10!}\frac{8!}{5!3!}=\frac{4!2!5!8!}{10!5!3!}.$$

Doctor Rick approved, with a nudge:

That is correct, but do you not want to express the final result as a fraction in lowest terms? The 5! cancels with the 5! in the denominator; 4!/3! = 4; 10!/8! = 10·9; and there’s a bit more that can be done.

Completing the answer, and expressing it a little differently, we can say that the numerator is $$\require{cancel}4!2!5!{8\choose5}=\frac{4!2!\cancel{5!}8!}{\cancel{5!}3!}=\frac{4!2!8!}{3!}=4\cdot2!8!,$$ so the probability is $$\frac{4\cdot2!8!}{10!}=\frac{4\cdot2!}{10\cdot9}=\frac{8}{90}=\frac{4}{45}.$$

Finishing the second way

Doctor Rick had more to say:

I said I would show you my alternative solution method, so I will do so, even though you have not completed the work by simplifying the fraction.

As I suggested, there are just four pairs of positions for the youngest two (A and B): the first in order can be in position 1, 2, 3, or 4, with the other in position 7, 8, 9, or 10 respectively. And either of A or B could be first, for a total of 4×2 = 8 possible positions for A and B.

This compares with 10×9 = 90 possible positions for A and B in the unrestricted case (one of ten positions for A, then one of the remaining nine positions for B).

The positions of the remaining eight learners can be chosen in the same way in either case, so they do not affect the probability. Thus the probability that A and B are separated by exactly five learners is 8/90 = 4/45. That’s the answer you should get the other way.

We could take into account everyone’s position, by multiplying the 8 ways to place A and B by the \(8!\) ways to place the other 8 kids, and then dividing by the \(10!\) ways to arrange everyone: $$\frac{8}{10\cdot9}=\frac{8\cdot\cancel{8}\cdot\cancel{7}\cdot\cancel{6}\cdot\cancel{5}\cdot\cancel{4}\cdot\cancel{3}\cdot\cancel{2}\cdot\cancel{1}}{10\cdot9\cdot\cancel{8}\cdot\cancel{7}\cdot\cancel{6}\cdot\cancel{5}\cdot\cancel{4}\cdot\cancel{3}\cdot\cancel{2}\cdot\cancel{1}}=\frac{8}{10\cdot9}=\frac{4}{45}.$$ But he’s avoided the big numbers, “pre-canceling” the \(8!\) by just ignoring the locations of the other 8, which are irrelevant. That makes the work a lot simpler: $$\frac{4\cdot2}{10\cdot9}=\frac{4}{5\cdot9}=\frac{4}{45}.$$

The argument above may seem a little loose, and we want to be careful with probability problems — it’s so easy to overlook something. However, if we write the numbers of successful outcomes and total outcomes as 4×2×8! and 10! respectively, the ratio (which is the probability we seek) is just as I said above.

Thulani approved:

Great thinker indeed. I had to read your solution twice to notice that factorials, permutations and combinations are an overkill in this problem, careful thoughts simplify it profoundly.

I did simplify the fraction anyway but did not post it. I will focus on the other possibility of at least 5 learners in between. I’ve learnt a lot. Thanks again.

As a side note, the program I was working on did confirm the answer. although not so efficient, I went through all possible combinations but counted only those whose distance between the smallest positions is 6 {(1,7), (2,8), (3,9), (4,10)}.

For some counting problems, a brute-force calculation by listing everything would take too long; but when you can do it, it can increase confidence in the more thoughtful methods. And multiple methods are even better.