I like looking a little deeper into problems; here we’ll find that although the problem is simple if you take it on its own terms, those terms are actually impossible. Does it matter?
P(A) = 0.47 and P(A∩B) = 0.34 … but can they?
The question came from Louis, a teacher, in mid-May:
Refer to original question attached.
When we try to work out how many black marbles and white marbles, we found initial assumption might be incorrect.
If it is wrong, how to fix it?
We’re told some probabilities, and need to use them to find a conditional probability,
I answered, initially missing Louis’ subtle concern:
Hi, Louis.
The problem looks valid to me, at least on the surface; I do get an answer that checks out.
The key idea is that
P(A and B) = P(A) * P(B | A)
Taking A = first is black, and B = second is white, we are given P(A and B) = 0.34 and P(A) = 0.47, and want to find P(B | A):
P(B | A) = P(A and B) / P(A) = 0.34 / 0.47 = 0.7234
This is a simple application of the definition of conditional probability: $$P(B|A)=\frac{P(A\cap B)}{P(A)},$$ and we are given exactly what we need. (One might wonder, however, how one would happen to know those two probabilities!)
But in doing that, I was missing the details of what you said:
When we tried to work out how many black marbles and white marbles, we found initial assumption might be incorrect.
Evidently you found that there is no combination of marbles that could yield these probabilities. They clearly don’t expect you to worry about that. But let’s see what happens if you do.
The problem doesn’t ask anything about what marbles there are; you are expected to accept their numbers and use them, without looking deeper. Evidently either Louis and his class felt it was necessary to know what was in the jar in order to answer the question, or they were just curious.
After the first marble is selected, and assuming it was black, then for the second draw, all the white marbles are still there, but there is one less black (and therefore one less total). We can do some algebra to try to find the original numbers:
If we start with x black and y white marbles, then P(A) = x/(x+y), and P(B | A) = y/(x+y-1). So we want
x/(x+y) = 0.47 ==> x = 0.47(x+y) ==> 0.53x = 0.47y ==> y = 0.53/0.47 x = 1.12766x
y/(x+y-1) = 0.7234 ==> y = 0.7234(x+y-1) ==> 0.7234x – 0.2766y = 0.7234
Substituting,
0.7234x – 0.2766(1.12766x) = 0.7234
0.41149x = 0.7234
x = 1.758
y = 1.12766*1.758 = 1.982
Since those aren’t whole numbers (and x isn’t at all close), this situation can’t happen. Is that your concern?
In general, we wouldn’t expect to get exact answers, so we might round to the nearest whole numbers (or to other nearby numbers, as we’ll see later), and see if they work; here, we might round both x and y to 2. But then $$P(A)=\frac{2}{2+2}=\frac{1}{2}=0.5\ne0.47,$$ and $$P(B|A)=\frac{2}{2+2-1}=\frac{2}{3}=0.666…\ne0.7234.$$ And $$P(A\cap B)=\frac{1}{2}\cdot\frac{2}{3}=\frac{1}{3}\ne0.34.$$
You might think these numbers are close enough that some adjustment could make it work; but if you try other numbers, you’ll see that you can’t get the values they give, accurate to the number of decimal places they give.
Here is what I get if I try small total numbers of marbles with the number of black set to get P(A) as close as possible to 0.47:
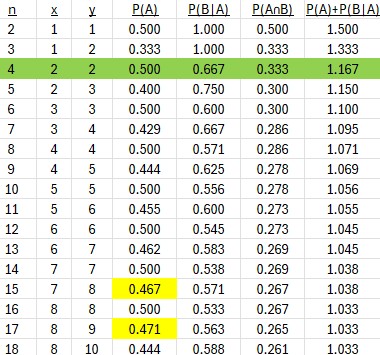
\(P(A)\) does not have a value that would round to 0.47 until \(n=15\); meanwhile, \(P(A\cap B)\) is getting smaller and smaller, moving away from the given value of 0.34.
You might also have seen this on a simpler level: If we have only black and white, and the numbers are reasonably large, then the probabilities of black on the first draw and white on the second (regardless of what happened on the first) should add up to something close to 1, and 0.47 + 0.72 = 1.19 > 1. So it feels wrong from the start.
I say this because for large numbers of marbles, removing a black would not make a big difference in \(P(B)\), so \(P(B|A)\approx P(B)\); and \(P(A)+P(B)=1\) (if we were choosing with replacement). Even using our small numbers, 2 and 2, we had \(P(A)+P(B)>P(A)+P(B|A)=1.167\), and we can see that sum decreasing toward 1 in the table above.
Clearly they didn’t derive their numbers from any actual numbers of marbles, but just picked random values for the probabilities. This is probably not an uncommon situation; I certainly see many problems in which we are given totally invented data that has nothing to do with reality – especially in computer homework programs that have to generate random numbers for each try. They just want a problem that sounds more specific and “real” than “one event has a probability of 0.47, and so on”. I’m generally inclined to forgive them.
But technically, the question is a conditional: IF these probabilities were given, THEN this would be the other. The condition is not required to be valid to say this is true! The result does follow from the givens, if they could be real.
So it isn’t technically wrong to give our answer of 0.7234, because that’s what would be true if the given data could ever occur. Sort of …
But that’s not really a good excuse; this is another of those problems where someone who chose to do something other than the obviously intended work would find himself in trouble, and I don’t like those.
From time to time we get a problem that good students would get “wrong”, because they think for themselves. Sometimes, too, we see problems that have no actual solution for reasons similar to what we are seeing here. I find them interesting, but troubling. (In this post, I called this “a trap for the wary, rather than for the unwary”.)
Now, we can consider fixing the problem; I suspected a likely difficulty, so I tried more marbles with the same \(P(A)\):
But let’s try one more thing: If we make up a similar problem that is entirely valid, will it test students’ knowledge well?
Suppose we say that there are 100 marbles, 47 black and 53 white. Then
P(A) = 47/100 = 0.47
P(B | A) = 53/99 = 0.53535
P(A and B) = P(A) * P(B | A) = 0.47 * 0.53535 = 0.251616
If we kept to two significant digits, we’d be giving the student P(A) = 0.47 and P(A and B) = 0.25, and the answer would be
P(B | A) = P(A and B) / P(A) = 0.25 / 0.47 = 0.53
That seems reasonable; but the fact that 0.53 = 1 – 0.47 might lead to right answers for wrong reasons.
That is, a student could get the right answer by calculating the probability that the first marble is white, rather than the conditional probability that the second marble is white. These are actually different numbers, but rounding makes them look the same. It’s not a good test question.
Bottom line: It’s an interesting exercise to dig behind the problem as you have, but you should let the students know that in general they should take a problem at face value and assume that the most direct solution is what they want.
In particular, trying to find the number of marbles is both the long way to an answer, and leads them into a swamp that the problem’s author didn’t even consider, where the “correct” answer changes to “this can’t happen!”.
On the other hand, a valid version of the problem seems to enter a different swamp, where imprecise numbers mess up the problem.
Can we change it to a valid problem?
But Louis wanted to pursue correcting the problem:
Now we understand it is a practical question, not theoretical one. It’s possible to get 0.34 and 0.47 when marbles number is big enough.
We are keen on theoretical analysis.
Let x/(x+y) = k, y/(x+y-1) = b.
What kind of k and b, and their relationship will be, given x and y are whole numbers?
I would say that the problem as stated is theoretical, as the author has ignored whether it can actually occur; presumably Louis wants to treat it as a “practical” (real) problem.
But what I showed is that there is no number of marbles that will work, for these particular numbers; in fact, increasing the number makes it worse. So as a “practical” problem, it is faulty.
Now he wants to find a way to choose (or recognize) values of \(k=P(A)\) and \(b=P(B|A)\) such that the equations \(\frac{x}{x+y}=k\) and \(\frac{y}{x+y-1}=b\) can be solved for integers x and y. It isn’t clear how one might recognize whether k and b have such a solution, though we might find some necessary conditions; of course, we can instead just start with x and y and find k and b, but even that, as we’ll see, isn’t so simple.
[Since in the problem we are given \(P(A)\) and \(P(A\cap B)\), it might be better to take those as our two variables. We’ll do that eventually, calling them \(k=P(A)\) and \(h=P(A\cap B)\).]
I replied:
I don’t expect to find a nice answer to your question; I’m not sure what form such a relationship would take.
Of course, we can generalize my work and solve for x and y for any k and b; I get
x = kb/(k+b-1)
y = (b-kb)/(k+b-1)
If these numbers are integers (or close to integers, so that rounding them should yield values for k and b close to whatever was given), then the scenario assuming those numbers is possible. As I pointed out, for example, k + b must be close to 1, since
k + b = x/(x+y) + y/(x+y-1) ≈ x/(x+y) + y/(x+y) = 1
unless x and y turn out to be very small, so that the difference becomes significant.
And the point of my example was that for real situations, k and b would have to be given to more precision in order to make a viable problem.
So we should be able to find pairs k, b that “work” by starting with pairs x, y of integers, as long as they round nicely. That could be an answer to his question. And we’ll get to that. But first I tried using the one criterion I’d suggested:
Take another example: Suppose we were given P(A) = k = 0.65 and P(B | A) = b = 0.36, whose sum is close to 1. Then we would find that $$x=\frac{kb}{k+b-1}=\frac{(0.65)(0.36)}{0.65+0.36-1}=\frac{0.234}{0.01}=23.4\\y=\frac{b-kb}{k+b-1}=\frac{0.36-(0.65)(0.36)}{0.65+0.36-1}=\frac{0.126}{0.01}=12.6$$
These are not whole numbers, but we can round them to 23 and 13 and hope that they are the numbers of marbles.
The fact that 23.4 and 12.6 are not very close to 23 and 13 suggests there may be trouble if we assume that these are the actual numbers of marbles!
But I didn’t choose 0.65 and 0.36 randomly; in fact I obtained my k and b from x = 15 and y = 8, which gave k = 0.652173913 and b = 0.363636, and rounded them.
Using 23 and 13 would yield k = 0.638888889 and b = 0.371428571, which do not round to 0.65 and 0.36, but to 0.64 and 0.37! If I had rounded to k = 0.652 and b = 0.364, the reverse formula would correctly yield 15 and 8. This is what I mean by needing more precision.
In particular, using the latter numbers, we get $$x=\frac{kb}{k+b-1}=\frac{(0.652)(0.364)}{0.652+0.364-1}=14.833\approx15\\y=\frac{b-kb}{k+b-1}=\frac{0.364-(0.652)(0.364)}{0.652+0.364-1}=7.917\approx8,$$ which are correct.
How we round makes a big difference.
But at least we now have an example of a valid problem: If we are given that \(P(A)=0.652\) and \(P(A\cap B)=P(B|A)P(A)=(0.364)(0.652)=0.237\), then we can not only get the correct answer, $$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{0.237}{0.652}=0.36349\dots\approx0.363,$$ but we could, if we chose, take the long way, by calculating \(x=15\) and \(y=8\), and then $$P(B|A)=\frac{y}{x+y-1}=\frac{8}{15+8-1}=\frac{8}{22}=0.3636\dots\approx0.364,$$ which I will call good enough.
I tried other pairs:
It can be even worse. If I started with x = 73 and y = 54 (chosen at random), then I would get k = 0.57480315 and b = 0.428571429. But if I round those to k = 0.57 and b = 0.43, the calculation of x and y fails, because I have to divide by 0. So then you might wrongly tell me that my problem did not represent whole numbers of marbles!
I’m discovering these things by playing with a spreadsheet that implements these formulas and rounding. You might find that interesting to explore.
Another perspective
It may be better to work with the quantities actually given in the problem, \(P(A)\) and \(P(A\cap B)\), and calculate x and y directly from those.
Let $$k=P(A)=\frac{x}{x+y}$$ and $$h=P(A\cap B)=P(A)P(B|A)=\frac{x}{x+y}\cdot\frac{y}{x+y-1}=\frac{xy}{(x+y)(x+y-1)}.$$
Solving these for x and y, we get $$x=\frac{hk}{h-k\left(1-k\right)}\\y=\frac{h\left(1-k\right)}{h-k\left(1-k\right)}$$
Putting this into a spreadsheet that takes x and y as input, generates h and k, rounds them to get the probabilities that would be given in the problem, and then regenerates x and y for comparison, I find similar results to those above for \(x=15\) and \(y=8\): This yields \(k=0.65\) and \(h=0.24\) after rounding to two places; but when we then solve for x and y, we get \(x=12\) and \(y=7\). If we check these by calculating h and k from them, we get \(k=0.63\) and \(h=0.25\), so we would not trust this. But if we did use those values we’d get $$P(B|A)=\frac{y}{x+y-1}=\frac{7}{12+7-1}=\frac{7}{18}=0.3888\dots\approx0.39.$$
If, instead, we round to three places, we get \(x=15\) and \(y=8\), and find we can trust them. Using them, as before, we get $$P(B|A)=\frac{y}{x+y-1}=\frac{8}{15+8-1}=\frac{8}{22}=0.3636\dots\approx0.364.$$
The correct answer, of course, would be $$P(B|A)=\frac{h}{k}=\frac{0.237}{0.652}=0.36349\dots\approx0.363.$$
My other example, \(x=73\) and \(y=54\), works better this way. Rounding to two places again, we’d be given \(k=0.57\) and \(h=0.25\) for our problem, from which we would find \(x=29\) and \(y=22\), which are very wrong, yet on checking do bring us back to \(k=0.57\) and \(h=0.25\), so we would consider ourselves correct. Our answer, then, would be $$P(B|A)=\frac{y}{x+y-1}=\frac{22}{29+22-1}=\frac{22}{50}=0.44.$$ This agrees with the answer we’d get directly from the given values, $$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{0.25}{0.57}=0.4385\dots\approx0.44.$$
So this (evidently worse) case works better than the other!
Who needs rounded decimals? Use fractions!
Louis had a good insight:
I have tried and feel it is too hard to continue.
I fixed the question simply to change the numbers:
Answer is 2/3.
Please confirm if it’s okay.
Thanks!
He’s changed the numbers, and made them fractions rather than decimals, which suggest exactness, and don’t call for rounding. We don’t know how he chose these numbers, but I have a guess!
I responded:
First, I’ll solve the new problem directly:
P(first black and second white) = 4/15
P(first black) = 2/5
P(second white | first black) = P(first black and second white) / P(first black)
= (4/15) / (2/5) = 4/15 * 5/2 = 2/3
As a rounded decimal, this is 0.67. (But your problem shouldn’t ask for a decimal answer.)
This is all the problem requires. What if we want to do more?
Now I’ll try figuring out how many marbles there are:
If there are n marbles, then there are (2/5)n black marbles and (3/5)n white marbles.
On the second draw, there are n-1 marbles, of which (3/5)n are white.
So P(second white | first black) = [(3/5)n] / [n – 1] = 2/3, so
(3n)/5 = 2/3 (n – 1)
3(3n) = 10(n – 1)
9n = 10n – 10
10 = n
There are initially (2/5)10 = 4 black and (3/5)10 = 6 white marbles.
As a check,
P(first black) = 4/10
P(first black and second white) = 4/10 * 6/9 = 4/15, which is correct.
So the scenario is possible.
Of course, we don’t really need to do the second part.
Alternatively, we could have found the numbers of marbles directly from the given probabilities, without first solving the problem as stated:
Using the formulas from before, given \(h=\frac{4}{15}\) and \(k=\frac{2}{5}\),
$$x=\frac{hk}{h-k\left(1-k\right)}=\frac{\frac{4}{15}\frac{2}{5}}{\frac{4}{15}-\frac{2}{5}\left(1-\frac{2}{5}\right)}=\frac{\frac{8}{75}}{\frac{4}{15}-\frac{6}{25}}=\frac{\frac{8}{75}}{\frac{2}{75}}=4$$
$$y=\frac{h\left(1-k\right)}{h-k\left(1-k\right)}=\frac{\frac{4}{15}\left(1-\frac{2}{5}\right)}{\frac{4}{15}-\frac{2}{5}\left(1-\frac{2}{5}\right)}=\frac{\frac{4}{25}}{\frac{4}{15}-\frac{6}{25}}=\frac{\frac{4}{25}}{\frac{2}{75}}=6$$
Now we answer the question: $$P(B|A)=\frac{y}{x+y-1}=\frac{6}{4+6-1}=\frac{6}{9}=\frac{2}{3}.$$
This approach includes finding the numbers of marbles as an essential part, so it feels more natural.
Now, presumably Louis created the problem by choosing 4 black and 6 white from the start; using fractions eliminated the difficulties we’ve found with rounding. That makes it a nice problem.
But I still had an interest in that rounding issue:
Now, what if you stated the problem using (rounded) decimals, as in the original?
Then we’d do this:
P(first black and second white) = 0.27
P(first black) = 0.4
P(second white | first black) = P(first black and second white) / P(first black) = 0.27/0.4 = 0.675
Rounded, this is 0.68.
Rounding results in a small deviation from 2/3; but this is what would be considered the correct answer, based on what was given.
And what if we try finding the number of marbles again?
If there are n marbles, then there are 0.4n black marbles and 0.6n white marbles.
On the second draw, there are n-1 marbles, of which 0.6n are white.
So P(second white | first black) = [0.6n] / [n – 1] = 0.675, so
0.6n = 0.675(n – 1)
0.6n = 0.675n – 0.675
0.675 = 0.075n
n = 0.675/0.075 = 9
There are initially (0.4)9 = 3.6 black and (0.6)9 = 5.4 white marbles.
These round to 4 and 5, which we guess to be the actual numbers, with some trepidation (because they are not close to integers).
But then
P(first black) = 4/9 = 0.444…
P(first black and second white) = 4/9 * 5/8 = 0.2777…
These don’t round to the given values.
So the scenario seems wrong?
Again, rounding causes trouble. A good problem (with decimals) would be one where minimal rounding is needed.
Approximating probabilities by decimals is problematic, isn’t it? That, again, is a reason we don’t tend to consider finding the number of marbles in such a problem, but just trust the author (rightly or wrongly!).
Let’s consider one last question: Is there any reason a fraction-based problem might not be a good problem?
The only thing I can see is that keeping exact fractions might result in big numbers. For example, our 15 black, 8 white case gives
$$k=P(A)=\frac{x}{x+y}=\frac{15}{15+8}=\frac{15}{23}\\h=P(A\cap B)=\frac{15(8)}{(15+8)(15+8-1)}=\frac{120}{506}=\frac{60}{253}.$$
That would make for a slightly ugly problem.
Another consideration is that, knowing the probabilities are exact, we might be tempted to use a different kind of reasoning. For example, in this case, we know that the total number of marbles is a multiple of 23, and since \(253=23\times11\), we might see that the real denominator (before simplifying) must be \(23\times22\), confirming that the total is exactly 23, and the number of black marbles is 15. Then the answer is \(P(B|A)=\frac{23-15}{22}=\frac{4}{11}\). But if a student works it out that way, they deserve full credit!
If we chose a larger number of marbles, we’d get even larger numbers. And my experimentation revealed even worse things that can happen than we’ve seen (think, negative numbers).
But give this problem a try:
A jar contains black and white marbles. Two marbles are chosen without replacement. The probability of selecting a black marble followed by a white marble is 0.19. The probability of selecting a black marble on the first draw is 0.25. What is the probability (to two significant digits) of selecting a white marble on the second draw, given that the first marble drawn was black?
How many marbles are there?


