We’ve been talking about the oddities of zero, and I want to close with another issue similar to last week’s \(0^0\). All our questions will be essentially identical apart from details of context: “We know zero factorial equals 1; but why?” This isn’t nearly as controversial as the others, but will bring closure to the topic; and I’m always interested in seeing multiple perspectives on the same fact.
Combinations: Two people shaking hands
Our first question is from 1998:
Why does 0 factorial equal 1? Why does 0! = 1? Is there a reason or is this like anything to the power of 0 = 1 - there is not a reason?
Recall that “factorial” means the product of descending integers, and is written as \(n!=n(n-1)(n-2)\dots1\). For example, \(5!=5\cdot4\cdot3\cdot2\cdot1=120\). Since we are multiplying factors from n down to 1, it makes sense (mostly) that \(1!=1\), since we just start and end with 1; but how can you count down from 0 to 1??
Furthermore, the first use of the factorial is to answer permutation problems: \(n!\) is the same as \(_n\text{P}_n\), the number of ways to arrange all of n objects a row. It makes sense that there is one way to arrange one object (\(_1\text{P}_1=1!=1\)); but how can you arrange no objects?
Doctor Sam answered, starting with Denise’s suggestion:
Denise, You are correct that 0! = 1 for reasons that are similar to why x^0 = 1. Both are defined that way. But there are reasons for these definitions; they are not arbitrary. You cannot reason that x^0 = 1 by thinking of the meaning of powers as "repeated multiplications" because you cannot multiply x zero times. Similarly, you cannot reason out 0! just in terms of the meaning of factorial because you cannot multiply all the numbers from zero down to 1 to get 1. Mathematicians *define* x^0 = 1 in order to make the laws of exponents work even when the exponents can no longer be thought of as repeated multiplication. For example, (x^3)(x^5) = x^8 because you can add exponents. In the same way (x^0)(x^2) should be equal to x^2 by adding exponents. But that means that x^0 must be 1 because when you multiply x^2 by it, the result is still x^2. Only x^0 = 1 makes sense here.
This idea was discussed as part of What Do Exponents Mean?, as well as in Anything to the Zero Power: Why 1? As in many situations involving zero, we ultimately just have to make a new definition, but we do it so that it remains consistent with existing rules.
But we’ll see later how, in a sense, we can multiply zero numbers!
In addition to permutations, the factorial is used in combinations, as we explained in Permutations and Combinations: An Introduction.
In the same way, when thinking about combinations we can derive a formula for "the number of ways of choosing k things from a collection of n things." The formula to count out such problems is n!/k!(n-k)!. For example, the number of handshakes that occur when everybody in a group of 5 people shakes hands can be computed using n = 5 (five people) and k = 2 (2 people per handshake) in this formula. (So the answer is 5!/(2! 3!) = 10).
The basic idea behind this formula is that each of the 5 people shakes 4 hands for a total of $$_5\text{P}_2=\frac{5!}{(5-2)!}=\frac{5\cdot4\cdot3\cdot2\cdot1}{3\cdot2\cdot1}=5\cdot4=20$$ shakes; but this counts each shake twice (\(_2\text{P}_2=2!=2\) times), so we have to divide by \(2!\). So the general formula is $$_n\text{C}_k=\frac{n!}{k!(n-k)!}$$
Here are those $$_5\text{C}_2=\frac{5!}{2!(5-2)!}=\frac{5!}{2!3!}=\frac{5\cdot4\cdot3\cdot2\cdot1}{(2\cdot1)\cdot(3\cdot2\cdot1)}=\frac{5\cdot4}{2\cdot1}=10$$ handshakes (the red lines, joining points representing people):
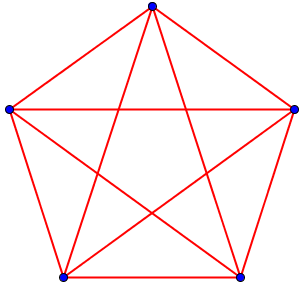
Now suppose that there are 2 people and "everybody shakes hands with everybody else." Obviously there is only one handshake. But what happens if we put n = 2 (2 people) and k = 2 (2 people per handshake) in the formula? We get 2! / (2! 0!). This is 2/(2 x), where x is the value of 0!. The fraction reduces to 1/x, which must equal 1 since there is only 1 handshake. The only value of 0! that makes sense here is 0! = 1. And so we define 0! = 1.
Here is that $$_2\text{C}_2=\frac{2!}{2!(2-2)!}=\frac{2!}{2!0!}=\frac{2\cdot1}{(2\cdot1)\cdot(1)}=1$$ handshake:
![]()
If \(0!\ne1\), we wouldn’t get that answer. We make the definition so the formula remains correct.
Combinations: choosing everything
Here is a 1997 question:
Why is 0! 1? My question is: Why is zero factorial 1? I've looked in encyclopedia and my math book, but I can't seem to find the answer. Please help me.
Doctor “Statman” answered with the same explanation in disguise:
Hi Kimberly, Here is a mathematical reason for 0! to be 1. Let's count how many ways there are to get 3 heads (H) and 2 tails (T) out of 5 tosses of a coin. Let's write down all the possibilities: HHHTT There are 10 sequences of 3 heads and 2 tails. Instead HHTTH of writing them all down, we could have calculated: HTTHH 5!/(3!2!) = 120/(6*2) = 10 TTHHH HHTHT HTHTH THTHH HTHHT THHTH THHHT Let's do the same thing for 4 heads and 1 tail: HHHHT There are 5 ways, and this matches 5!/(4!1!) = 120/24 = 5 HHHTH HHTHH HTHHH THHHH There is only one way to get all 5 heads, and that is HHHHH Now the formula would say 5!/(5!0!) and if 0! is anything other then 1 then this answer would not be equal to 1, as it should be. This formula is called a binomial coefficient. It means that if you want to choose r objects from n objects, and you don't care about the order of the r objects, then the number of ways to do that is n!/r!(n-r)!
How does the same formula we used for handshakes (combinations) apply to sequences of heads and tails? We are choosing r of the n positions in the sequence to be heads.
In general, if \(r=n\), so that we are choosing all members of a set of n, which can be done in one way, we get $$_n\text{C}_n=\frac{n!}{n!(n-n)!}=\frac{n!}{n!0!}=\frac{1}{0!},$$ and this will only equal the expected 1 if we define \(0!=1\).
Combinations: choosing nothing
Another question is from 1999:
Zero Factorial My question is this: Why does 0! = 1? I have no idea about this one. My Algebra II teacher admits that he doesn't know. I have also asked the two physics teachers. Everyone tells me 'because it does'. I don't like having to accept this logic because I am the kind of person who usually needs a reason for things. I would really appreciate any help you could provide. Thank you.
Doctor Tom answered, using combinations in yet another way:
"Because it does" isn't a bad answer. Actually, what happens is this - if you define it to be anything else, then lots of other formulas in math don't work when you plug zero into them.
Here's a simple example: How many ways can you choose k things out of a set of n things? For example, how many ways can you choose 2 things out of a set of 4? The answer is 6. If the 4 things are A, B, C, and D, here they are:
AB, AC, AD, BC, BD, CD
In general, the formula for "how many ways can you choose k things from a set of n?" is given by:
n!
--------
k!(n-k)!
In our example, n = 4; k = 2:
4! 24
-------- = ---- = 6.
2!(4-2)! 2(2)
This is \(_4\text{C}_2=\frac{4!}{2!(4-2)!}=\frac{4\cdot3}{2\cdot1}=6\). It’s also the number of handshakes among four people.
How many ways can you choose zero things? Exactly one way, right? Just take none of them - anything else you do is wrong. So if k = 0, the formula should give 1, right?
n! 1
-------- = ----- = 1
0!(n-0)! 0!
If 0! is anything but 1, the formula doesn't work.
There are LOTS of examples like this, but most of them require a lot of math.
This may be a little less satisfying than the other way, because this example uses “nothing”, which feels a little less real; but it is true. There is only one subset of {A, B, C, D} that has no elements, namely {}. Alternatively, you could say that we are choosing 4 elements to leave out, which, as we saw, can be done only one way.
The Ask Dr. Math FAQ: three reasons
The three answers we’ve seen are all equivalent. Before we look at the next question, I want to take a look at our FAQ, which provides background for it in the form of additional explanations:
0! = 1
Contributed by “Dr. Floor,” Floor van Lamoen
Why does 0! = 1 ?
Usually n factorial is defined in the following way:
n! = 1*2*3*…*n
But this definition does not give a value for 0 factorial, so a natural question is: what is the value of 0! ?
This is why the answer is not obvious; he gives three reasons to say the answer is 1:
Following a pattern backward
A first way to see that 0! = 1 is by working backward. We know that:
1! = 1 2! = 1!*2 2! = 2 3! = 2!*3 3! = 6 4! = 3!*4 4! = 24We can turn this around:
4! = 24 3! = 4!/4 3! = 6 2! = 3!/3 2! = 2 1! = 2!/2 1! = 1 0! = 1!/1 0! = 1In this way a reasonable value for 0! can be found.
This is much like one approach we took for \(x^0=1\), where we saw that we could get the next whole power by multiplying by the base, and therefore could get the previous whole power by dividing by the base. Here, we get the next factorial by multiplying by the next number, and get the previous factorial by dividing by the current number.
But we can’t continue this for negative numbers, since that would require dividing by 0. In fact, in contrast to negative powers, negative integers don’t have factorials at all.
Recursive definition
We can restate what we just did as a recursive formula, providing an alternate definition:
How can we fit 0! = 1 into a definition for n! ? Let’s rewrite the usual definition with recurrence:
1! = 1 n! = n*(n-1)! for n > 1Now it is simple to change the definition to include 0! :
0! = 1 n! = n*(n-1)! for n > 0
Much as we restated the definition of \(x^n\) to start at \(n=0\), we have made a small change and now \(0!\) is part of the “natural” definition. Whenever you multiply repeatedly, you are effectively starting with 1.
Combinations: choosing everything or nothing
That redefinition is really all we need; but he also briefly shows the combinations we looked at above, not as proof, but as a further motivation:
Why is it important to compute 0! ?
An important application of factorials is the computation of number combinations:
n! C(n,k) = -------- k!(n-k)!C(n, k) is the number of combinations you can make of k objects out of a given set of n objects. We see that C(n, 0) and C(n, n) should be equal to 1, but they require that 0! be used.
n! C(n,0) = C(n,n) = ---- n!0!So 0! = 1 neatly fits what we expect C(n, 0) and C(n, n) to be.
Our explanations above filled in a lot of details.
The Gamma function
Although it is not necessary, we can also answer a bigger question: Do non-integers have factorials? In a sense, they do, but it requires another new definition (and some deep calculus).
Can factorials also be computed for non-integer numbers? Yes, there is a famous function, the gamma function Γ(z), which extends factorials to real and even complex numbers. The definition of this function, however, is not simple:
∞ Γ(z) = ∫ x^(z-1) e^(-x) dx 0Note that the extension of n! by Γ(z) is not what you might think: when n is a natural number, then Γ(n) = (n-1)!
The gamma function is undefined for zero and negative integers, from which we can conclude that factorials of negative integers do not exist.
In the FAQ, this function is called G; I have used the actual Greek letter gamma (Γ) instead. Here is the actual definition of the gamma function: $$\Gamma(z)=\int_0^\infty x^{z-1}e^{-x}dx$$ If you know about integration by parts, you can show that $$\Gamma(z+1)=z\Gamma(z)$$ and that $$\Gamma(1)=1;$$ this gives us a recursive formula equivalent to our formula for the factorial – which also implies that \(0!=\Gamma(1)=1\).
But this is beyond my goal for this post; someday we’ll look into what we’ve said more deeply about the gamma function.
An empty product can make sense
We’ll close with this question from 2008:
An Informal Argument for Why 0! = 1 I don't understand why 0 factorial is 1.
It’s the same question we’ve had all along, but we’ll get a different kind of answer this time.
Doctor Tom answered again:
Hi Miggy,
Thanks for writing to Doctor Math!
There are some good technical reasons why 0! = 1, but you may not find any of them convincing. You can read about some of them on our Frequently Asked Questions page:
Why Does 0! = 1?
http://mathforum.org/dr.math/faq/faq.0factorial.html
Here's a more informal argument that might make sense. People often have trouble with 0! being 1 because they think that they are multiplying no numbers, or only 0, so it must be 0. How can an "empty product" be worth 1?
When people have expressed doubt about \(x^0=1\), this has often been their main point. They probably have the same thing in mind here.
Let me go at this by analogy, starting with an "empty sum". You know how to add 4 things or 3 things or 2 things, right? What if you just add 1 thing? Shouldn't that just be the thing? How about zero things? Shouldn't that just be zero? For example, suppose you have 5 numbers and you divide them between two friends. What is the sum of the numbers? It should be the sum of the numbers A has plus the sum of the numbers B has, right? What if you give them all to A? Shouldn't the same method work? Well, that means that you need to say that the sum of B's zero numbers is 0 so that the total sum of A and B is still correct. So we agree that an "empty sum" has a value of 0.
For example, if we split the sum \(2+4+3+5+1=15\) into two parts like \((2+4+3)+(5+1)=9+6\), we know that the sum of the two parts will be 15 again. If the second part contains none of the numbers, \((2+4+3+5+1)+{\color{Red}{()}}=15+{\color{Red}?}\), the sum of no numbers has to be 0.
This doesn’t generally bother anyone.
Similarly, suppose you again divide 5 numbers between two friends. What is the product of the numbers? It should be the product of the numbers A has times the product of the numbers B has. But if you give them all to A, you'd better call the product of the zero numbers that B has 1. If you call it 0, then multiplying A's product by B's product will be 0, not the correct total product. So it makes sense to agree that an "empty product" must have a value of 1.
Let’s change the sum above to a product: \(2\times4\times3\times5\times1=120\). If we split it into two parts, we still get the same product: \((2\times4\times3)\times(5\times1)=24\times5=120\). If we make the second part empty, we still get the same product: \((2\times4\times3\times5\times1)\times{\color{Red}{()}}=120\times{\color{Red}?}\). So that empty product must equal 1. (If it were 0, as many people guess, the product would be 0!)
So 4! = 4x3x2x1: you're multiplying 4 numbers. 1! = 1: you're multiplying 1 number. What should 0! be? You're multiplying zero numbers, and as we just saw, that had better be 1, right? I hope this helps you understand why 0! must be 1.
We briefly discussed empty products (and empty sums) in the post on \(x^0\).

Proposition:
0! ⇒ ∄
Proof:
Γ(n) = (n-1)!
Γ(n) = (n-1) × Γ(n-1)
Γ(1) = 0! = 0 × Γ(0) ⇒ ∄, because Γ(0) is undefined!
Eureka!
Hi, Nim.
Your logic is incorrect, and you have omitted some important details.
(Though it isn’t important, your notation is also wrong; “∄” means that what follows does not exist, so it can’t be written alone as you did twice. It doesn’t mean “it doesn’t exist”.)
First, you are missing essential conditions for your premises:
But more important,
is invalid logic, essentially the fallacy of denying the antecedent.
The fact that you can express a quantity in an invalid way (by starting with something that is undefined) does not imply that it doesn’t exist. It only means that that way of determining it is invalid.
The reality is that 0! = Γ(1) = 1 by definition. See Wikipedia, for example: $$\Gamma(1)=\int_0^\infty t^{1-1}e^{-t}dt=1$$
So 0!=1! ??? That isn’t logical .
Even 1! Isn’t logical. You can’t multiply 1x? not 1. You don’t do 2!= 2×2 !!
Better to make it undefined like divide by 0.
Hi, Danny.
I take it you haven’t actually read what we wrote here, which shows the logic. Please take the time to do so, and if you still disagree, answer our reasoning.
If you’re claiming that the factorial of two different numbers, 0 and 1, can’t be equal, you’re just assuming that it has to be a one-to-one function. That does not have to be true for a function to be defined! For example, we define \(f(x)=x^2\) for all real numbers, but \(f(-1)=f(1)\), so it is not one-to-one. But it is a perfectly well-defined function, and a very important one. If I said it wasn’t logical that \((-1)^2=(1)^2\), I would not be thinking logically.
And leaving 0! undefined, as we mentioned several times, would mean that some important calculations couldn’t be done.