(A new question of the week)
A question in September, about graphing a horizontally-stretched cosine function, led to a long conversation. Between a typo in the problem and some inside-out thinking, this surprisingly non-routine problem led to some good mind-stretching! I have edited this down considerably by removing distractions from the main ideas, but it still shows how far we go in guiding a student to find their own way to a solution.
Here is the question, from Frankie:
For the question below I’m unsure how to get the answers for (a) and (c).
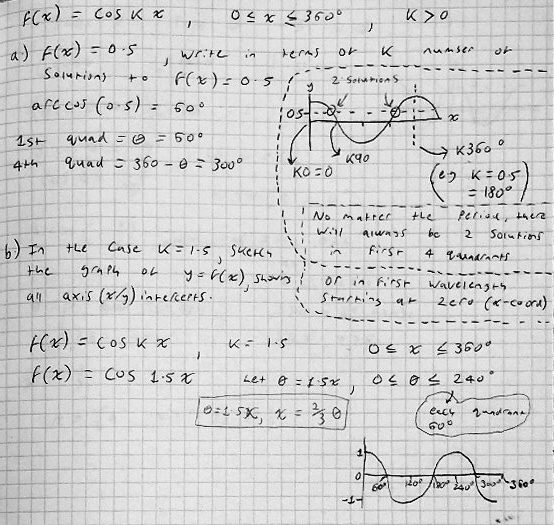
For (a), wouldn’t stretching the cosine graph be able to give any infinite number of solutions the larger you make k ? If so how could you say how many solutions/roots there are?
And lastly for (c) how would you go about finding the range of values for k, as I haven’t had this demonstrated in class and cannot find any examples in my textbook.
(In the original question, Frankie misquoted the problem, which led to some confusion. Showing the actual problem as given often helps us get to the main issues more quickly! But in this case, even the original problem is faulty.)
Part (b): Graphing with a stretch
Doctor Rick answered, correcting the problem and suggesting a starting point:
Hi, Frankie, thanks for writing to the Math Doctors.
I believe there is a typo in the problem. The inequality 0 ≤ k ≤ 360 makes no sense to me. First of all, that would mean that k is qualified twice; there would be no need for the additional qualification “k is a positive constant.” Second, if there is no condition on x, then the equation has an infinite number of solutions, and questions (a) and (c) make no sense. Also, it is implied that k is an angle — up to 360° — so that x would be a pure number. I really doubt that this is intended.
So I’m going to assume that the condition is 0 ≤ x ≤ 360. Thus the graph of y = f(x) will extend only from x = 0 to x = 360, rather than going on forever in both directions.
You don’t indicate that you had any trouble with part (b), so I’d like to see what you did with that part. It can be a good start in understanding what the other two parts mean and how to solve them. I say this because one good way to start “playing” or “experimenting” with a problem is to try a specific case, and letting k = 1.5 is a specific case. From that, we can try to generalize to any value of k.
Regarding your question about (a), you’re right that the number of solutions will increase as the value of k increases. Therefore the answer to (a) will not be a number; it will be an expression in k. That expression should give the number of solutions you got in (b) when you plug in 1.5 for k.
Part (c) is the reverse of part (a), so without solving it yet, I would guess that the answer will involve using the expression from part (a) to write an equation in k, and solving that equation. However, since the result is to be a “range of possible values”, not just one value, there must be something else going on here. I’m pretty sure I know what it is, but I want you to discover that for yourself.
So again, please show me your answer to (b) and how you thought that through, then give (a) a try and tell me what you run into.
You may have noticed that in (a), k is an integer, while in (b) it is not, and (c) doesn’t mention integers. Frankie had initially omitted the word “integer”, changing the problem slightly. But (b) is still a good place to start.
Frankie wrote back:
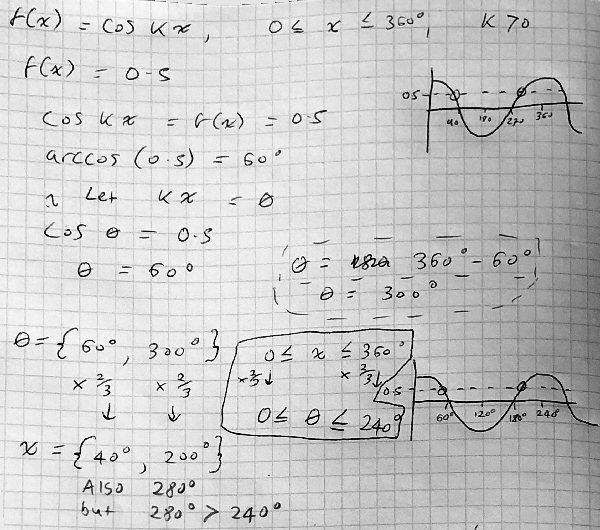
For part (b), I had a graph of cosine with a stretch in the x axis with a scale factor of 2/3 so the first zero at 60 degrees, then 180, 300 etc.
For part (a), I’m still a little lost. From where my head is, I have an equation cos kx = 0.5. I then do arccos(0.5) to get principal value of 60 degrees and from here I’m assuming (which may be wrong) that kx=60 or something along those lines ?
Here is the graph of \(f(x) = \cos(1.5x)\), showing how the graph of \(f(x) = \cos(x)\), dotted, has been “stretched” (actually compressed) by a factor of \(\frac{2}{3}\):
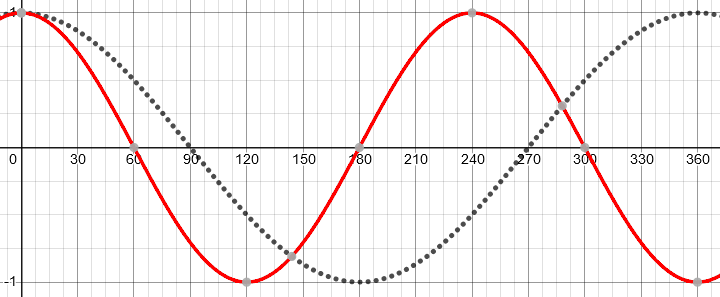
Frankie is correct about where the zeros are, as shown, and has a good start on part (a).
Doctor Rick replied:
Thanks for getting back to me.
I’d like you to extend your work on (b) by finding the solutions of the equation f(x) = 0.5. That is, find the points on the graph for which y = 0.5. The number of solutions you find will be the answer to part (a) when k = 1.5. (When I talked before about part (a) being a generalization of part (b), I was actually thinking that part (b) asked you not just for the graph but for what I’m asking you to do now.)
(I still haven’t worked the problem all the way through; I want to walk through it along with you.)
(Part (a) actually restricts k to be an integer, but that wasn’t yet clear in the actual discussion.)
Frankie responded:
For part (b) would the answers be either 60 and 300 degrees on the normal cos graph, or 40 and 200 on the modified graph?
Here is the same graph showing y = 0.5, showing that Frankie is right about the first two intersections in each case:
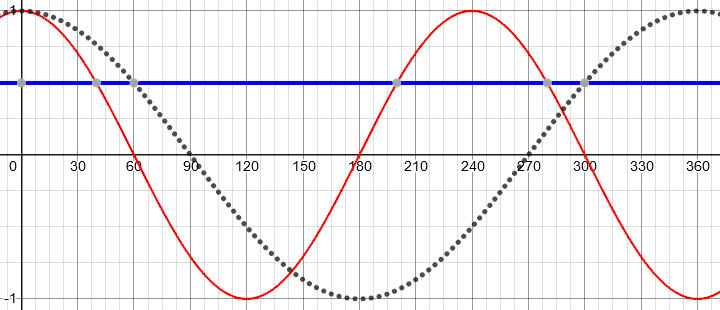
Part (a): Solving within an interval
Doctor Rick responded:
You are saying, I believe, that the solutions to cos(kx) = 0.5, for 0 ≤ x ≤ 360°, are 60° and 300° when k = 1 (the “normal” graph as you called it, that is, y = cos(x)), and 40° and 200° when k = 1.5. That’s mostly correct; you missed one solution in the second case. Can you find it? In addition, we’ll need to talk about how you got your result, because it’s the “how” that will enable us to generalize from what we’re doing now to part (a).
Are you familiar with descriptions of an infinite family of solutions, such as the following?
x = 40 + 240n, for any integer n
If you are, could you find all solutions to cos(1.5x) = 0.5, expressed in this form? I just showed you half the solutions. Then, can you use this result to find all the solutions for x that are between 0° and 360°? Show me your work, not just your solution.
Frankie answered:
Okay, good. Here is my work:
Frankie has correctly found the two angles with the given cosine, within the first cycle of the unstretched graph, but is having trouble applying the restriction on x correctly.
Keeping track of the restriction
Frankie tripped over the transformation; so Doctor Rick focused on that part:
I notice that you may have confused yourself a bit in your work. Let me go over it with you to see what’s happening. You are trying to solve the equation
cos(kx) = 0.5, subject to the constraint 0 ≤ x ≤ 360°
You made a change of variables (not a bad idea), letting θ = xk, and then you solved the equation
cos θ = 0.5
You found a first solution, θ1 = arccos(0.5) = 60°. Then you found a second solution, θ2 = 360° – θ1 = 300°. So far, so good.
Now, you change back to the original variable, x:
θ in {60°, 300°}
θ = kx = 1.5x
x = θ/k = (2/3) θ
x1 = (2/3) 60° = 40°
x2 = (2/3) 300° = 200°
Still good! Now we get to some work you put in a box. Starting from the domain restriction on x,
0 ≤ x ≤ 360°
you correctly obtain a restriction on θ:
0 ≤ θ ≤ 240°
Then you write “Also 280°”, which I believe refers to a third solution for x. Presumably you added 360° to θ1, obtaining the angle θ3 = 420° which is coterminal to θ1; then you multiplied this by 2/3 to get x3 = 280°. Still good! But you didn’t write explicitly that this is a value of x, so you got confused and compared it with the maximum value of θ, 240°! You should be comparing x = 280° with the maximum value of x, 360°, which tells us that 280° is a valid solution to the equation.
You really made a pretty small error, but it’s important.
Now we need to try to generalize. To move in that direction, can you start listing all the solutions for x, ignoring the restriction? As I think you know, this will involve writing all angles that are coterminal to θ1 or θ2. In my last message, I wrote an expression that represents all angles coterminal with 40°, so you only need to write a similar expression for angles coterminal with 200°.
Once we have that, we can use each expression to write an inequality that says a particular solution meets the condition. That’s where we’re headed.
I think Doctor Rick misinterpreted the inequality on θ. Since \(x=\frac{2}{3}\theta\), if \(0\le x\le 360\), then \(0\le \frac{2}{3}\theta\le 360\) and therefore (multiplying everything by \(\frac{3}{2}\), \(0\le \theta\le 540\). Frankie multiplied everything by \(\frac{2}{3}\) instead.
But the main point is correct: 280 is a valid solution of the problem.
Frankie answered:
I think if the scale of the graph is changed then you would just scale these up/down to size (using the appropriate scale factor) after working out the initial values of x for sin(x) = theta .
I notice that Frankie is still talking about the number of solutions “in first 4 quadrants”, that is, in one cycle, and not looking at the restriction of x to [0, 360]. The variables x and θ are still being confused, as \(0\le x\le 360\) is being used to describe one cycle of the untransformed function, which should really be \(0\le \theta\le 360\), while \(0\le \theta\le 240\) is taken to refer to one cycle of the transformed function, which should be \(0\le x\le 240\). But these are not prominent here.
Counting cycles
Doctor Rick approved of the graph, showing implications Frankie may have missed:
The graph you show for part (b) is correct: in the domain of 0° to 360°, the function goes through 1 1/2 cycles. Notice that the number of cycles (or periods) in 360° is 1.5 = k. That might be a clue as we try to generalize to any k!
Also, notice that if you add the line y = 0.5 to your figure, it intersects the graph in 3 points — confirming that there are three solutions to cos(1.5x) = 0.5. This contradicts your claim in part (a) that there are always two solutions! We have to figure out what went wrong in your reasoning.
I can’t tell exactly what you were thinking because you are rather terse in this section, but I suspect you made essentially the same mistake I pointed out last time: mixing up x and θ when considering the domain. Your graph shows two solutions in 0° ≤ θ ≤ 360°, which is true, but we’re interested in how many solutions there are in 0° ≤ x ≤ 360°.
You marked on your graph that the end of one period of the function is k · 360°. Is that correct? One period corresponds to θ going from 0° to 360°; θ = kx, so x = θ/k and a change in θ of 360° corresponds to a change in x of 360°/k, not k · 360°. Now, if one period of f is 360°/k, how many periods are there in the domain of f, with width 360°? If you get this right, it will agree with what you drew for part (b).
We are almost at the solution for part (a), once we get past the confusion of the two variables.
Frankie replied,
For part (a) where I said that there are only two solutions what I meant was that in the first wavelength (i.e. 360 degrees in (a) or 240 degrees in (b) there is only 2 solutions. So for cos1.5x there is three solutions because there is 3/2 wavelengths of cos. And for my graph of (a) I think it should be 360/k that was my mistake.
We’re definitely getting there; the restriction of \(0\le x \le 360\) covers \(\frac{3}{2}\) of the 240° period (“wavelength”) of our function for the case \(k=1.5\). For part (a), we just need to know the general answer in terms of k.
After some discussion of this, Doctor Rick explained the meaning of part (a) in detail:
Let’s review exactly what the problem said (with the typo corrected):
f(x) = cos kx, 0 ≤ x ≤ 360°, where k is a positive constant.
(a) In the case when k is a positive integer, write, in terms of k, the number of solutions to the equation f(x) = 0.5.
What constitutes a solution to the equation f(x) = 0.5? It’s a value of x, in the domain of f, such that f(x) = 0.5. (If x is not in the domain of f, then f(x) is not defined, so it cannot equal 0.5.) So we are to find the number of distinct values of x in the interval 0 ≤ x ≤ 360° for which cos kx = 0.5.
Let’s also pull together some of the things you have determined:
- The first period of f ends at x = 360°/k.
- In the case k = 1.5, f(x) goes through 1.5 periods between x = 0 and x = 360°.
- There are 2 solutions to the equation in each period.
If you can use the first bullet point to generalize the second bullet point, then combine the generalization with the third bullet point, you’ll have the answer to part (a).
Frankie responded:
I was misunderstanding the question to just be essentially how many solutions are there to f(x) however from the way it’s worded and the way you explain it I’m assuming that the number of solutions and k will be related, as k changes all x values. From the second bullet point, k = 1.5, there are three solutions so for that it is 2k solutions but I’m unsure if this is in general and how to work this out for different questions. But from the first bullet point if 360/k is the period and there are 2 solutions in each period maybe I could set up an equation like 360/k = period, period has 2 solutions so 360/k =2 ⇒ 360 = 2k solutions but I’m not certain this is right.
Doctor Rick replied:
Yes, there are 2k solutions when k is a positive integer. You’re right not to be sure that this is general, if all you’re seeing is that when k = 1.5, there are 3 solutions. We need to generalize the method, not just the result. I’ll show you how, since we’re so close.
We have established that the period of the function f(x) = cos(kx) is 360°/k. This is a fraction 1/k of the width of the domain of our function, 0° to 360°, so k periods fit into the domain.
We have also established that within each period there are two solutions to the equation f(x) = 0.5. Therefore the number of solutions is twice the number of periods, or 2k. That’s all there is to it (after we did all the preparatory work). Now I hope there is no need for uncertainty.
Part (c): For what k are there exactly 3 solutions?
In parallel with the discussion we’ve seen, Frankie had also been attempting part (c), including some false starts I will omit. Eventually they got to this:
I have made a second attempt here with what I think is the right method for (c).
Doctor Rick replied:
Your second attempt is good! Let me clean it up by using standard terminology, being explicit about the change of variables, and using more algebra, which is concise and precise.
You found that the first four solutions of the equation cos θ = 0.5 are 60°, 300°, 420°, and 660°. For full generality, we could write all solutions of this equation as
θ = 60° + n·360° or 300° + n·360°, where n is any integer
using the fact you have noted that adding 360° (any number of times) to a solution of the equation produces another solution. Now we replace θ with kx:
kx = 60° + n·360° or
kx = 300° + n·360°, where n is any integer
We can solve these equations for x:
x = 60°/k + n·360°/k, or
x = 300°/k + n·360°/k, where n is any integer
The first two solutions of the first form are 60°/k and 420°/k; the first two solutions of the second form are 300°/k and 660°/k. There is nothing wrong with doing the same thing for each solution separately, as you did; for instance
kx = 60°
x = 60°/k
So we have the first four solutions for the general case of any k. We need to find all values of k for which only the first three are in the restricted domain:
So now we want to apply the restriction on the domain of f, and find what restrictions to put on k so that there are exactly three solutions. As you say, we require that the third solution, 420°/k, be in the domain, and thus
420°/k ≤ 360°
But we don’t want the fourth solution, 660°/k, to be in the domain, because then there would be too many solutions!
360° < 660°/k
Solving these inequalities, using the fact that k > 0 so we can multiply by it without changing the direction of the inequality, we obtain
k ≥ 420°/360° = 7/6
k <660°/360° = 11/6
And that’s the answer to part (c):
7/6 ≤ k < 11/6
As I suggested last time, we can check for consistency with the particular case we found by extending part (b), by showing that k = 1.5 gives three solutions. Indeed, 7/6 ≤ 3/2 < 11/6, so we’re good.
Frankie:
Wow, thanks for clearing that up you’ve been a great help. Thankfully I can now say that there is no uncertainty in part a or c. Anyways thanks a lot for your help and I will make sure to take these methods with me in future.
Doctor Rick closed:
I’m glad we could help. I noticed that this problem is labeled “Gold”, which I suppose means it is particularly challenging. Such problems require clear thinking, and you can learn a lot about thinking clearly as you solve them. (In a way, that’s what math is really about: the art of clear thinking.)