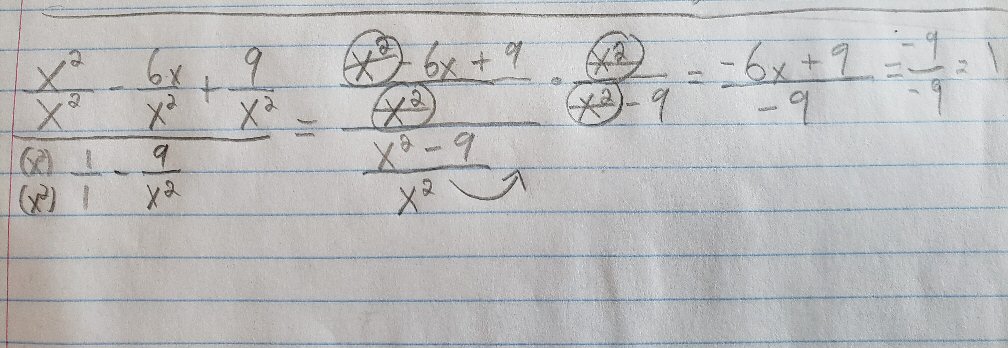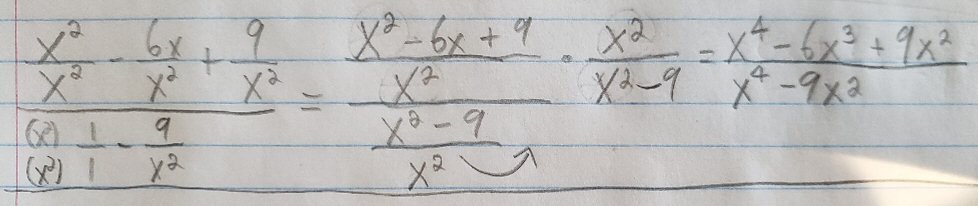(A new question of the week)
I have often said that calculus class is where many students finally learn algebra, because now algebra is an essential tool, not just something to learn for an exam. This is especially true of a nontraditional student, who may not have taken math recently, or may even be learning on his own. So quite often when we help a student with a calculus problem, much of our effort goes into guiding them through the algebraic parts of the work, correcting old misunderstandings or forgotten details. Here we’ll look at a limit problem that provided several opportunities to review algebra. (Almost none of what we discuss here will actually be calculus.)
A limit of a rational function
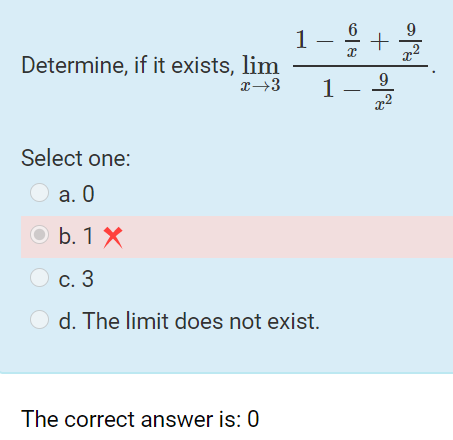
Here is the question, which came from Chase in late August:
I’m trying to figure out where my solution goes south. I’ve attached the problem and my solution. I come to the conclusion of 1 while the answer says 0. Do you see the flaw in my workflow?
I observe that the problem is (intentionally?) tricky, as it is written in the form we would put it into if we were taking the limit as x approaches infinity, so that all the fractions approach 0, and the limit would be 1. But instead x approaches 3; and Chase didn’t take the bait, but changed all terms to use the common denominator by \(x^2\), added them to turn the expression into the quotient of two fractions, and then rewrote that as a product of fractions, $$\frac{\frac{x^2-6x+9}{x^2}}{\frac{x^2-9}{x^2}} = \frac{x^2-6x+9}{x^2}\cdot\frac{x^2}{x^2-9}$$ That is excellent work so far. But then something goes wrong …
An error in simplification
Doctor Rick answered:
Hi, Chase. I can’t follow your work in regard to the circled x2‘s. What does that mean?
The last valid step I see, if I am interpreting it correctly, is to change the division by ((x2 – 9)/x2) into multiplication by x2/(x2 – 9). When we do that, we should get
x2 - 6x + 9 ----------- x2 - 9All I can think is that you thought you could subtract x2 from the numerator and the denominator. If that’s what you thought, you were wrong! For instance, if I have the fraction 3/4 and subtract 2 from the numerator and denominator, I get 1/2, which is not equivalent to 3/4.
What you need to do in order to simplify this algebraic fraction is to find a common factor of the numerator and denominator, and “cancel” that factor from both. That is, divide — not subtract — the same quantity in the numerator and denominator. This step will require factoring the numerator and denominator. Can you do that?
I often see students who are generally good at algebra make this mistake of “canceling terms”, as Chase has done by crossing out the \(x^2\) where it occurs in numerator and denominator. Proper “cancellation” doesn’t mean just crossing off the same thing in two places, but thinking about what operation it takes to do that, as Doctor Rick has said here, and making sure that is legal in the context. You can’t subtract from both parts of a fraction (crossing off terms), but you can divide both parts (crossing off factors). So before you can simplify a fraction, you need to look for factors.
Can we ignore the variable?
Chase replied:
After the multiplication step you say we should get,
x^2 - 6x + 9 ------------ x^2 - 9But if that was the answer, then we ignored the second x^2 that came before 9? A common factor I see without all the Xs is 3.
The mention of 3 as a common factor “without all the x‘s” suggests that Chase is not factoring the numerator and denominator as a whole, but looking for common factors of terms, ignoring the variable.
Step by step
Doctor Rick wrote back, narrating Chase’s work from the start so that every step will be as clear as possible, including the reason it is correct:
If by “the second x2 that came before 9″, you mean the x2 in the expression x2 – 9, I definitely did not ignore that one — but you may not be following what happened to the first x2. Let me go over the work thus far in more detail.
The expression we started with, whose limit we would like to find, was
6 9 1 - --- + -- x x2 ------------ 9 1 - -- x2You correctly gave all the terms in the numerator a common denominator, so that they could become a single fraction:
6 9 x2 6x 9 x2 - 6x + 9 1 - --- + -- = -- - -- + -- = ----------- x x2 x2 x2 x2 x2Likewise you gave all the terms in the denominator a common denominator, and made them a single fraction:
9 x2 - 9 x2 - 9 1 - -- = -- --- = ------ x2 x2 x2 x2
So the numerator and the denominator are good.
Then, as I noted last time, you correctly recognized that the new expression is a division of one fraction by another, which is equivalent to multiplication of the first fraction by the reciprocal of the other:
x2 - 6x + 9 x2 - 9 x2 - 6x + 9 x2 ----------- ÷ ------- = ------------ × ------ x2 x2 x2 x2 - 9
(We normally avoid using the multiplication sign “×” in algebra, to avoid confusing it with the variable “x“; but here I suspect Doctor Rick wants to carefully emphasize the operation (particularly as we continue below) because distinguishing multiplication from addition is a key to getting all of this right.)
Cross-canceling: “Nothing up my sleeves …”
Now we’re up to the step I did, in which I skipped a step, supposing you would follow it. Now that we’re multiplying fractions, we can use the concept of “cross-cancellation” — which is often misunderstood, so I’ll expand this next step so you can see what’s really going on — not some magic trick. I will first multiply the fractions by multiplying the numerators to get the new numerator, and multiplying the denominators to get the new denominator — but I won’t do any of the multiplication, just write out the instruction to multiply:
(x2 - 6x + 9) × x2 ------------------ x2 × (x2 - 9)
“Cross-cancellation” means crossing off those two lone \(x^2\)s even before writing this step; that’s a shortcut for all the thinking that follows, and can be done safely once you really understand why (and when) it can be done).
Now I’ll switch the order of the factors in the denominator — you may recall the “commutative property of multiplication” which says we can do this:
(x2 - 6x + 9) × x2 ------------------ (x2 - 9) × x2
This just lines up the matching (common) factors for the next step:
Next I’ll take a “backward” step, pulling this apart into a multiplication of two fractions — but not the same two fractions I started with:
x2 - 6x + 9 x2 ----------- × --- x2 - 9 x2
Why would we “unmultiply”? Because that second factor can be simplified greatly!
Now, I notice that the second fraction is a quantity divided by the same quantity, which is always 1 (as 2/2 = 1, 5/5 = 1, and so on). Multiplying a quantity (in this case, a fraction) by 1 is the same as doing nothing to it (we say 1 is the “multiplicative identity”), so we can just drop the fraction that’s equal to 1. And there go the x2‘s that you were wondering about!
x2 - 6x + 9 ----------- x2 - 9
In terms of cross-cancelling, we would just have done this: $$\require{cancel}\frac{x^2-6x+9}{\cancel{x^2}}\cdot\frac{\cancel{x^2}}{x^2-9} = \frac{x^2-6x+9}{x^2-9}$$
Factoring in order to cancel further
Now we need to talk about the next step. We will be doing the same sort of thing that we just did, when the numerator and denominator were both products. But the numerator and denominator aren’t products! In order to use the “canceling” idea, we will have to make them into products. That’s what we mean by “factoring”. We can only cancel factors (things that are multiplied by something else), not terms (something added to something else).
You said that “a common factor without all the x’s is 3.” We can’t ignore the x’s, though. If you were bothered that I seemed to ignore some x’s, then you should be bothered by your own statement.
That statement about a common factor referred, I believe, to the fact that, in \(x^2-6x+9\), if we dropped all the variables we would have just \(-6+9\), and both terms are multiples of 3. But the first term really has a coefficient of 1, which is not a multiple of 3, so in fact this polynomial has no numerical common factor. We need something more.
Factoring a polynomial is a complicated topic that I can’t go into in one message. If you have forgotten what you learned about this topic in algebra class, then you will need to go back and relearn it. There is no way around this; most of the work we do in calculus is actually algebra. I’ll point you to the Ask Dr. Math Archive, and a couple of respected math sites that go through this topic in a more systematic manner.
The “Learning to Factor” section of the Ask Dr. Math FAQ deals with both factoring of numbers and factoring of polynomials. You will mostly need the latter, of course. For the numerator you want to factor a quadratic; for the denominator, you’ve got a special, simpler type of quadratic called a difference of squares, and there is special help with that.
The PurpleMath site has help with “Factoring Quadratics: The Simple Case” which is all you’ll need for now. For the simpler case in the denominator, see “Special Factoring: Differences of Squares“.
MathsIsFun is another site that can guide you in the “how-tos” of topics such as Factoring Quadratics.
Give those a try.
Chase didn’t ask for further help with factoring, so probably this reminder was enough. Let’s finish the problem.
Finishing the limit
As was hinted, we can factor the numerator as a trinomial, and the denominator as a difference of squares: $$\frac{x^2-6x+9}{x^2-9} = \frac{(x-3)\cancel{(x-3)}}{(x+3)\cancel{(x-3)}} = \frac{x-3}{x+3}$$
Now we can take the limit: $$\lim_{x\to 3}\frac{x-3}{x+3} = \frac{3-3}{3+3} = 0$$
Since the function, after simplifying, is continuous at \(x=3\), we can just substitute. What happened here was that the simplification yields an expression that is equal to the original except at \(x=3\), where the canceled factor is zero, and the limit is unaffected by any single value.
So we have finished the problem, and got the answer we were told was correct.