Let’s look at a nice little challenge: to find a cubic function with maximum and minimum at given locations – without using calculus. We’ll explore how to solve it with graphing software, and using algebra in a couple ways, and finally with calculus. And, surprise! They all give the same answer, though the results look different each time.
Finding a cubic without calculus
Here is the question, from a teacher, Mary Jo, in mid-May:
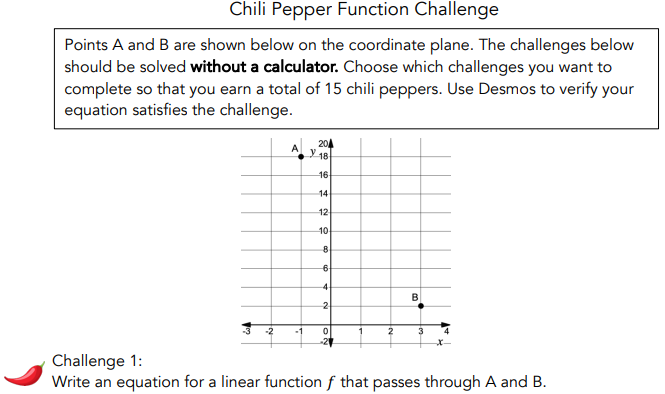
Dear Doctor Math, This was a challenge problem in the AP Precalculus Math Medic curriculum Chili Pepper Challenge. You are given two points, (-1, 18) and (3, 2), and asked to find various types of functions that pass through these points.
The hardest challenge was to find a cubic that passes through these points, assuming that (-1, 18) is a relative maximum and (3, 2) is a relative minimum, without calculus (this is a precalculus course).
I figured that the point of inflection was (1, 10) (using average values) but you still need a 4th point to get an equation. The suggestion was to play around with your graphing calculator for an answer. It seems to me that there are infinite answers to this problem. The one presented as a possible answer was
.5x3 – 1.5x2 – 4.5x + 15.5.
I found something similar by testing out various 4th points.
Is there a mathematical way to do this? I found your blog post Max and Min of a Cubic Without Calculus – The Math Doctors which seems to be what I want but backwards; but I could not puzzle my way through using your post. Can you answer my question directly!
You can tell I am a math nerd – my husband (an engineer) and I are puzzling though this problem over my Mother’s Day breakfast! Thanks for any clarification you can provide.
Here is a graph showing what is required, which you could sketch from the description (but which I’ve made from their answer):
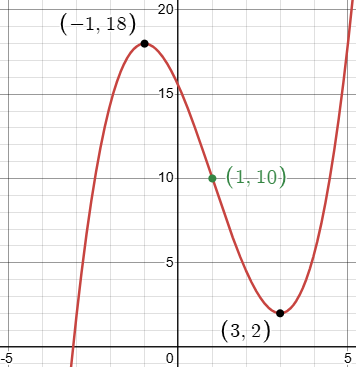
We see the curve passing through the two given points, which are respectively a local (or relative) maximum and a local (relative) minimum, or turning points; and Mary Jo’s third point, the point of inflection where the curve changes from curving downward to curving upward. (This term is taught in calculus, and probably not in precalculus, though maximum and minimum are.) This is what it is because for any cubic of this sort, the point of inflection is exactly between the max and the min: $$\text{POI}=\frac{\text{max}+\text{min}}{2}=\frac{(-1,18)+(3,2)}{2}=\left(\frac{-1+3}{2},\frac{18+2}{2}\right)=\left(1,10\right)$$ Precalculus students are unlikely to know this fact; we’ll look into that later.
Here is an image of the actual problem as I found it just now:
…

Since a cubic function \(y=ax^3+bx^2+cx+d\) has four unknown parameters to “play with”, pure “investigation” might take a lot of work; but perhaps some intelligent preparation can make it easier. Let’s try doing that before we look for a purely algebraic approach.
Just playing
The point \((-1,18)\) tells us that \(a(-1)^3+b(-1)^2+c(-1)+d=18\), i.e. $$-a+b-c+d=18.$$
The point \((3,2)\) tells us that \(a(3)^3+b(3)^2+c(3)+d=2\), i.e. $$27a+9b+3c+d=2.$$
We can partially solve this system of equations, subtracting the first equation from the second to get \(28a+8b+4c=-16\); dividing by 4, \(7a+2b+c=-4\). So if we knew a and b, we would know that $$c=-4-7a-2b.$$
But then we can also find d, by plugging that into the first equation to get \(-a+b+4+7a+2b+d=18\), or \(6a+3b+d=14\), so that $$d=14-6a-3b.$$
So we only need to tweak a and b in $$y=ax^3+bx^2-(4+7a+2b)x+(14-6a-3b).$$
I did this, with two sliders in Desmos; it was not easy to make the graph behave as we want!

Playing a little more wisely
But Mary Jo mentioned an idea that leaves us much less to guess: We know three points the curve will pass through, so that will leave us with only one unknown parameter!
For a student insightful enough to include \(1,10)\), we also have \(a(1)^3+b(1)^2+c(1)+d=10\), i.e. $$a+b+c+d=10.$$
Plugging in our expressions for c and d above, this tells us that $$a+b-4-7a-2b+14-6a-3b=10$$ so that $$3a+b=0$$ and \(b=-3a\). Therefore $$c=-4-7a-2b=-4-7a+6a=-4-a,$$ Similarly, $$d=14-6a-3b=14-6a+9a=14+3a.$$
This reduces our general equation down to $$y=ax^3-3ax^2-4x-ax+3a+14,$$ which we can put into Desmos with one slider for a:
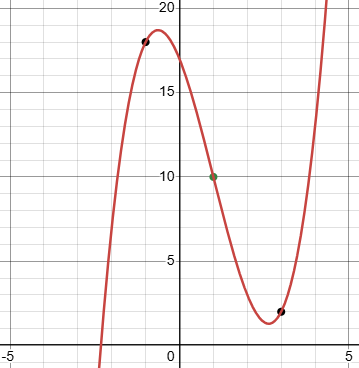

Drag the slider and you quickly find that \(a=0.5\) works!
Mary Jo may have done something different, and the authors of the challenge may have had less elaborate methods in view. But this shows what can be done with what amounts to “intelligent guess-and-check” coupled with technology.
Algebra: Shifting the point of inflection
But we want just algebra. And I hadn’t done this exploration; I’d done something else. I answered:
Hi, Mary Jo.
Yes, this is a fun problem. I’ve solved it by algebra (in fact, I haven’t yet done that with calculus, though in principle it’s straightforward). But since you know what real fun is (I define that as “challenging”), I don’t want to say too much. I’ll just describe my key ideas.
The answer is unique, and is what you said they gave.
I used your excellent starting point, that the point of inflection is (1, 10). But then I observed that a cubic is symmetric about its inflection point, so it’s an odd cubic, that is, y = ax3 – bx, shifted right 1 and up 10. So my function has the form
y = a(x-1)3 – b(x-1) + 10.
To avoid taking away the fun, I’ll just mention one other fact, from the post you found: If we shift the graph down, then x = 3 has to be a double zero — that is, we can divide by (x – 3) twice, getting zero remainder twice.
I hope this is enough to guide you, but not too much to still be an adventure.
A key idea here is that any cubic with max and min is just a stretched and shifted copy of the very same graph. In this case, if we shift the POI to the origin, we get this:
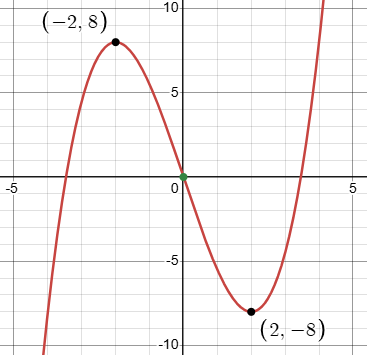
This is an odd function, that is, it is symmetrical about the origin (which is the POI). Its equation therefore has the form $$y=ax^3-bx$$ (The negative allows b to be positive. Experiment with this sort of graph a little, and you’ll see that.) Shifting this back to the location of the problem, with the POI at \((1,10)\), the equation becomes what I suggested: $$y=a(x-1)^3-b(x-1)+10$$
I don’t think we can easily prove what I’ve said here without calculus; it comes mostly from experience – experience a student can easily get by playing with a graphing tool.
Now, how do we find those coefficients?
Mary Jo didn’t respond; I hope that’s because this was all it took. But I was hoping for more discussion, so let’s talk about it now!
Moving the minimum
The key idea from the article Mary Jo had found is that if we shift a cubic so that a max or min is on the x-axis, then that zero will be a double root, corresponding to a squared factor:
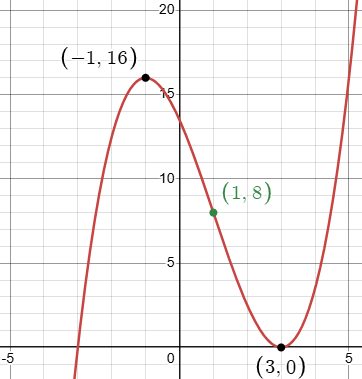
This is the function we want, shifted down 2 units, namely $$y=a(x-1)^3-b(x-1)+8.$$ Its equation must have the form $$y=a(x-c)(x-3)^2$$ where the coefficient a will be the same as above, and c is the single (negative) root.
There are several ways we might proceed from here. I’ll do what I did before writing my answer, as indicated by my hint. I first used the fact that \(f(-1)=16\), so $$a(-1-1)^3-b(-1-1)+8=16\\-8a+2b=8\\b=4a+4=4(a+1)$$
Next, I expanded the equation, with b replaced by this expression, making $$y=a(x-1)^3-4(a+1)(x-1)+8\\=a(x^3-3x^2+3x-1)-4(ax-a+x-1)+8\\=ax^3-3ax^2+3ax-a-4ax+4a-4x+4+8\\=ax^3-3ax^2-(a+4)x+(3a+12)$$
Since this must have \((x-3)^2\) as a factor, I used synthetic division twice and set the remainder to zero:
3 | a -3a -a-4 3a+12
| 3a 0 -3a-12
+---------------------
a 0 -a-4 | 0
3 | a 0 -a-4
| 3a 9a
+--------------
a 3a | 8a-4
Therefore we need $$8a-4=0\\a=\frac{1}{2}$$ and $$b=4a+4=6$$ Our equation is therefore $$y=a(x-1)^3-b(x-1)+10=\frac{1}{2}(x-1)^3-6(x-1)+10.$$
From the result of the divisions (the quotient being \(ax+3a\)), we can also see that the equation is $$y=\frac{1}{2}(x+3)(x-3)^2+2$$
Either of these forms would be a valid answer to the problem.
Checking that these are indeed the same, we can expand each:
$$\frac{1}{2}(x-1)^3-6(x-1)+10=\frac{1}{2}(x^3-3x^2+3x-1)-6(x-1)+10\\=\frac{1}{2}x^3-\frac{3}{2}x^2-\frac{9}{2}x+\frac{31}{2}$$
and
$$\frac{1}{2}(x+3)(x-3)^2+2=\frac{1}{2}(x^2-9)(x-3)+2\\=\frac{1}{2}(x^3-3x^2-9x+27)+2=\frac{1}{2}x^3-\frac{3}{2}x^2-\frac{9}{2}x+\frac{31}{2}$$
Both of these equal the given answer, \(.5x^3 – 1.5x^2 – 4.5x + 15.5\).
Algebra without the point of inflection
In writing this up, I’ve noticed other possibilities. Here’s an interesting one:
Suppose we know nothing about the point of inflection, but want to deal with both the max and the min in the same way.
If we call the function \(y=f(x)\), then since shifting down by 2 results in a double zero at \(x=3\), we see that $$f(x)-2=a(x-b)(x-3)^2;$$ and likewise, since shifting down by 18 results in a double zero at \(x=-1\), we have $$f(x)-18=a(x-c)(x+1)^2.$$ That is, $$f(x)=a(x-b)(x-3)^2+2=a(x-c)(x+1)^2+18.$$
Here b and c are the locations of the other intersections with \(y=2\) and with \(y=18\), respectively.
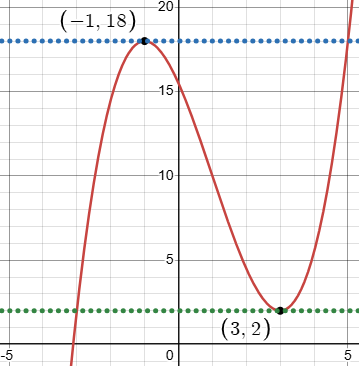
Now we have an identity: the following must be true for all x: $$a(x-b)(x-3)^2+2=a(x-c)(x+1)^2+18.$$
So we can expand both sides and set coefficients equal:
$$a(x^3-(b+6)x^2+(6b+9)x-9b)=a(x^3-(c-2)x^2+(1-2c)x-c)+16$$
$$b+6=c-2\\6b+9=1-2c\\-9ab=-ac+16$$
From the first two, we find that \(b=-3\) and \(c=5\). From the last, $$a=\frac{16}{c-9b}=\frac{16}{5-9(-3)}=\frac{1}{2}$$
This leaves us, again, with two forms that are equivalent: $$y=a(x-b)(x-3)^2+2=\frac{1}{2}(x+3)(x-3)^2+2\\y=a(x-c)(x+1)^2+18=\frac{1}{2}(x-5)(x+1)^2+18.$$ Check them out!
Using calculus after all
Let’s also try solving the problem using calculus, which may not be any easier!
We have a generic cubic, \(f(x)=ax^3+bx^2+cx+d\), whose derivative is \(f'(x)=3ax^2+2bx+c\). Setting \(f(-1)=18\), \(f(3)=2\), \(f'(-1)=0\), and \(f'(3)=0\), we get a system of four equations in four unknowns:
$$a(-1)^3+b(-1)^2+c(-1)+d=18\\a(3)^3+b(3)^2+c(3)+d=2\\3a(-1)^2+2b(-1)+c=0\\3a(3)^2+2b(3)+c=0$$
which simplifies to $$-a+b-c+d=18\\27a+9b+3c+d=2\\3a-2b+c=0\\27a+6b+c=0$$
We can subtract the first from the second to leave $$28a+8b+4c=-16,$$ and then subtract 4 times the third from that to leave $$16a+16b=-16,$$ and subtract the third from the fourth to leave $$24a+8b=0$$
These last two equations simplify to $$a+b=-1\\3a+b=0$$ so that $$a=\frac{1}{2}\\b=-\frac{3}{2}$$ Backtracking, $$c=-3a+2b=-3\left(\frac{1}{2}\right)+2\left(-\frac{3}{2}\right)=-\frac{9}{2}\\d=18+a-b+c=18+\frac{1}{2}+\frac{3}{2}-\frac{9}{2}=\frac{31}{2}.$$
Once again, we get $$y=\frac{1}{2}x^3-\frac{3}{2}x^2-\frac{9}{2}x+\frac{31}{2}$$
In summary, here are all the answers we’ve found:
$$y=0.5x^3 – 1.5x^2 – 4.5x + 15.5$$
$$y=\frac{1}{2}x^3-\frac{3}{2}x^2-\frac{9}{2}x+\frac{31}{2}$$
$$y=\frac{1}{2}(x-1)^3-6(x-1)+10$$
$$y=\frac{1}{2}(x+3)(x-3)^2+2$$
$$y=\frac{1}{2}(x-5)(x+1)^2+18$$
