A recent question led me to find a series of old questions, each answering it at a different level. All of them are worth presenting.
Here is Debarghya’s question:
Hello doctor, I have a silly question that came in my mind without any specific context. I know that I can ask question here fearlessly, so I am daring to ask this question.
I know that circle is a 2D shape as it uniquely defines a plane; but dimension is the number of independent parameters to specify an object. Since circle is a curved line having length (circumference) only, it is a 1D shape. Then which is correct?
On searching internet I found a statement (in Quora), “A circle together with its interior (i.e. the points inside it) is called a disk and is a 2-dimensional object. However, the circle itself is just the boundary of that disk, i.e. the points you would touch with your pencil if you were to move it around the circle. And that, i.e. the circle, is 1-dimensional.”
In this context surface of sphere is 2D but the space it occupies it is 3D. Is it correct?
I agreed with this conclusion, and then searched for our past answers to the same question, which I’ll expand here.
What are dimensions? Line, plane, circle
Let’s start with this basic question from 2001:
Dimensions
What are 1-dimensional, 2-dimensional, and 3-dimensional? What's the difference?
I answered:
Hi, Emily. Essentially, an N-dimensional object is one that requires N numbers to describe a location in it. A line is 1-dimensional, since one number, the distance from zero, tells you where you are. A plane is 2-dimensional, since you need x and y to locate a point.
The point on this line is fully identified by one number, 3, so the line is one-dimensional:
![]()
The point on this plane is fully identified by two numbers, \((3,2)\), so the plane is two-dimensional:
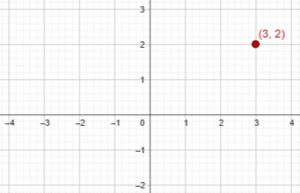
But each point in itself is just a point; we’ll see later that they have zero dimensions.
Although our overall question about a circle was not asked, I introduced it:
A circle (the curve itself, not the interior of it) is a 1-dimensional object in a 2-dimensional space, since although it takes 2 numbers to identify where in the plane a point on the circle is, only one number (the angle from a starting position) tells you where you are as long as you know you are on the circle.
The circle itself needs three numbers to identify it (location and size):
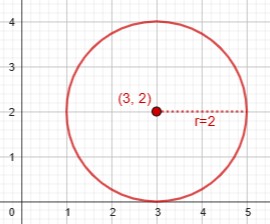
But a point on the circle requires only one number, so the circle is a one-dimensional figure:
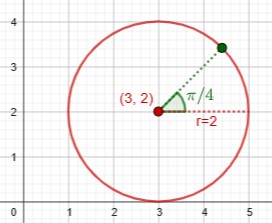
On the other hand, if we include the interior and ask about the disk, the location of a point requires two numbers (such as x and y, or r and θ), so the disk has two dimensions:
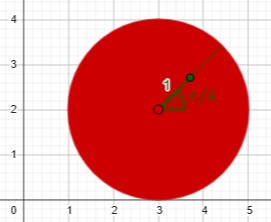
Then I referred to the following previous answer:
For 3 dimensions, here is a discussion I found in our archives: Is a Sphere 2-D or 3-D? http://mathforum.org/dr.math/problems/janice.8.8.96.html
How about a sphere?
Here is that reference, from 1996:
Is a Sphere 2-D or 3-D?
Dear Dr. Math: Is a sphere a two- or a three-dimensional object?
Doctor Jerry answered Janice:
Just to be certain we mean the same thing by sphere, a sphere is the set of all points in space (or R^3, which is Euclidean three space) at an equal distance from a fixed point. Not a solid ball.
Just as a circle is a curve, while a disk is a region including the interior, a sphere is a surface while a ball is a region including the interior. This is very important: What we are discussing is just the surface of a ball.
Although the sphere is a subset of three-dimensional space, it is a two-dimensional object. A circle can exist in either two-dimensional or three-dimensional space (or even higher-dimensional spaces), but it is a one-dimensional object. A line segment, which is one-dimensional, can be deformed into a circle. We can think of the line as elastic. A circular disk, which is two-dimensional, can be deformed elastically into a sphere.
Any curve can be thought of as a piece of a line that has been bent out of that line into two- or three-dimensional space.
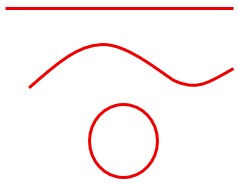
Each of these is still one-dimensional.
Similarly, any surface can be thought of as a piece of a (two-dimensional) plane even when it has been bent into three-dimensional space, or even closed back on itself.

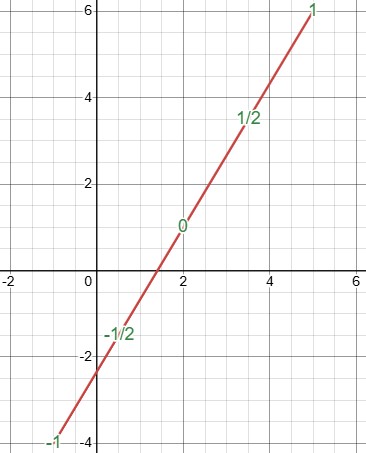
If you know about describing curves and surfaces parametrically, then, with certain restrictions, the dimension of the object is equal to the number of parameters required in its description. For example, a line in two-space can be described by the equations
x = 2+3t
y = 1+5t
The parameter t varies over a line or line segment, both of which are two-dimensional. Hence, the line in two-space is one-dimensional.
Here is that line, with values of the parameter marked:
We can do the same with a curve, such as this parabola, $$x=t\phantom{^2}\\y=t^2$$
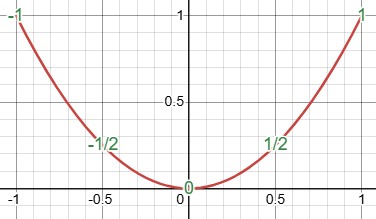
In each case, though the two coordinates x and y place the curve in two-dimensional space (a plane), the one parameter t makes the curve itself one-dimensional. It is an image of the t-axis.
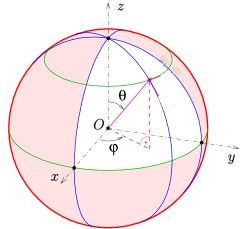
A sphere of radius a can be described by
x = a*cos(theta)*sin(phi)
y = a*sin(theta)*sin(phi)
z = a*cos(phi)
The parameters are phi and theta. So, the sphere is two-dimensional.
There are other, more complex definitions of dimension. These can be found in subject called topology, particularly in something called dimensional theory.
Here he is identifying a point on the sphere using spherical coordinates:
There are details about curves and surfaces beyond what we’ve said here, which are touched on in the next answer.
Getting technical
Doctor James also answered:
That's a very tricky question, and I can see exactly where your confusion lies. In one sense, we'd like to think that a sphere is a three-dimensional object, since we can take a ruler and measure its length, width, and height. But in another sense, it can't be a three-dimensional object because it has no volume (remember, a sphere is only the "skin of a ball," not the inside of the ball too), just like a flat plane has no volume.
The ambiguity is related to Doctor Jerry’s use of the word “describe”, which could be taken to mean either measuring the object in terms of the space it is in, or, as he used it, identifying locations within the object itself. Tricky, isn’t it?
If you've noticed, I've carefully avoided answering your question. :>. I can give you a technical answer that might not mean that much to you, but I'll try to explain it. A sphere is what is called a 2-manifold. A 2-manifold is a type of mathematical object, like a sphere, that looks like a plane if you zoom in far enough on it. Some other manifolds are a plane, the surface of a donut (also called a torus), and a 2-sheeted hyperboloid. A cone is NOT a 2-manifold, because it has a pointy part and no matter how much you zoom in on that point, the point won't start to look like a regular plane.
So a 2-manifold is a surface that behaves like a plane on small scales, though it may be bent and connected in odd ways on a large scale.
There are 1-manifolds too, and those look just like lines when you zoom in on them. Some examples of 1-manifolds are lines, circles, knotted circles, and lines that squirm around a bit in space. Two intersecting lines do NOT make a 1-manifold, because you can't zoom in on the intersection point and make it look like part of a regular line.
A 1-manifold is a curve that behaves like a line on small scales.
Mathematicians like to be formal about defining things sometimes, and so we define a 2-manifold as an object that is "locally diffeomorphic to a plane." This is a formal way of saying that every piece of a 2-manifold looks like a patch of a plane if you zoom in far enough. This kind of math is part of a subject called 'real analysis,' which is great fun.
He goes on, but you get the idea! The basic ideas are simple, but covering all possibilities can get complicated.
Two ways to look at it
This 2004 question is what I sent to Debarghya:
Two Interpretations of Dimensionality in Geometric Figures
I am a high school math teacher who could possibly be teaching geometry in the fall. I would like to teach the students about dimension. I understand that the x-axis alone is 1 dimensional. Throw in the y-axis and there are 2 dimensions. Add a z-axis and there are 3 dimensions. Overall I have a good understanding of dimensions. A line is 1 dimensional, a square or rectangle is 2 dimensional, and a cube is 3 dimensional. My question is what if you throw in parabolas or circles or the absolute value function, etc.? A parabola can only be drawn in 2-space, but lines are also drawn in 2-space unless the slope is 0 or does not exist. A circle is kind of like a parabola, but it is very much like a square, so I am thinking it is 2-dimensional. My conclusion is that the only 1 dimensional object is a straight line, and a point is 0 dimensional, but I am not confident that I am correct. Can you please clear this up for me?
We can see here echoes of the sort of issues we’ve seen already. Is the dimensionality of an object dependent on the space it is drawn in, or on something about itself? And is a circle or square a whole region, or just a curve like a parabola?
Intrinsic and extrinsic dimensionality
I answered:
Hi, Marianne. I think you have a very good understanding of this, and you are correct that a point is 0 dimensional. But there's lots more to dimensionality as well. The fact is that dimensionality can be taken in two ways: what we may call intrinsic dimensionality, which is essentially the number of dimensions it takes to identify the location of a point WITHIN the object, and extrinsic dimensionality, which is the number of dimensions of the (minimal) space it is "embedded" in. In the latter sense, a parabola is two-dimensional, since it can't be embedded in a Euclidean space of less than two dimensions; that is, it doesn't fit in a line. In the former sense, it is one-dimensional, since one number is enough to identify where you are along the parabola.
I think I more or less made up the terms, though the concept was a familiar one.
Note that the parabola can be thought of as a bent line; bending affects the extrinsic dimensionality, as I am calling it, but not the intrinsic dimensionality. The latter is therefore a topological property, one that doesn't depend on notions of straightness and length; it is what is described here:
We’ve seen this idea of topology above, and there will be more below. It is sometimes described as rubber-sheet geometry, dealing with properties that are unaffected by bending or stretching – that is, “invariant under continuous deformations”. I quoted a reference that gives a very informal depiction of dimensions:
http://mathworld.wolfram.com/Dimension.html To see how lower and higher dimensions relate to each other, take any geometric object (like a point, line, circle, plane, etc.), and "drag" it in an opposing direction (drag a point to trace out a line, a line to trace out a box, a circle to trace out a cylinder, a disk to a solid cylinder, etc.). The result is an object which is qualitatively "larger" than the previous object, "qualitative" in the sense that, regardless of how you drag the original object, you always trace out an object of the same "qualitative size." The point could be made into a straight line, a circle, a helix, or some other curve, but all of these objects are qualitatively of the same dimension. The notion of dimension was invented for the purpose of measuring this "qualitative" topological property.
Here we start with a point (0 dimensions), drag it to make a curve (1 dimension), then drag that to make a surface (2 dimensions), and then drag that to make a 3-dimensional region:

Here is a page on which I discussed some of these ideas, and also included a link to another page which includes another link. All of those are worth reading: Mobius Strips, Spheres, and Dimensionality http://mathforum.org/library/drmath/view/62980.html
We’ll be looking at that question next.
What I have called extrinsic dimension is a geometrical property, in which lengths and angles count. We call a triangle, for example, two-dimensional, because although the line segments that form it are one-dimensional, in geometry we are interested in the properties it has IN THE PLANE; we are interested not just in the object itself, but how it embeds. So it is an object we study as part of a plane, in two-dimensions.
It could also be said that in geometry we are not looking only at the edges of the triangle, but its angles and interior, the whole two-dimensional region.
Other sources
Looking for what else we’d said about dimensions, I found this:
This page on our site discusses the geometrical concept of a "two- or three-dimensional figure":
FAQ: Defining Geometric Figures http://mathforum.org/dr.math/faq/formulas/faq.figuredef.html "A two-dimensional figure, also called a plane or planar figure, is a set of line segments or sides and curve segments or arcs, all lying in a single plane. The sides and arcs are called the edges of the figure. The edges are one-dimensional, but they lie in the plane, which is two-dimensional."
This touches on both aspects:
Note that here the whole figure made up of segments and curves is considered two-dimensional because it lies in a plane, though the edges, even when curved, are acknowledged as one-dimensional.
So that article doesn’t disagree with what we’re saying here.
The trouble is that, although mathematicians tend to think about the topological idea of dimensions, anything before college tends to use only the geometrical perspective. From that point of view, your parabola is a two-dimensional figure, since you are drawing it on paper, and it doesn't lie along a line. A helix, really a one-dimensional object, would have to be called a 3-dimensional figure in this sense, since you can't draw it on paper except as an image of something in three-dimensional space.
One could say that at this level, we are looking at objects from the outside, extrinsically.
An additional complication arises when we talk about a circle, which we have defined as just the curve and not its interior, but then ask about its area, which is really the area of the disk formed by the circle and its interior. The names of most two-dimensional figures that are really one-dimensional objects are often used sloppily to refer to the corresponding two-dimensional object, like the disk, just because we are focusing not on the object itself at this level, but on the whole figure; and similarly for three-dimensional figures like a cylinder.
A mathematician talking to other mathematicians might talk only about the area of a disk, to avoid inconsistency; but we’re in the real world where such a distinction feels unnatural, so we live with the conflict!
Now, I made up the terms "intrinsic and extrinsic dimension"; they aren't standard terms, perhaps because we don't commonly bother thinking about both ideas at the same time! But here is one place where I found the same idea discussed:
I was glad to find at least one place where my invented terms were used, showing I wasn’t being unreasonable!
What is Topology? http://www.pepperdine.edu/seaver/natsci/FACULTY/KIGA/topology.htm "These objects are examples of curves in the plane. In some sense they are two dimensional since we draw them on a plane. In another sense, however, they are one dimensional since a creature living inside them would be only aware of one direction of motion. We might say that such shapes have extrinsic dimension 2 but intrinsic dimension 1."
I’ve linked to an archived copy of this old page. Today, I find a very nice discussion of the idea (again pointing out that it is not often taught in this sort of context) in this paper by Matthew N. Bernstein:
Before we move on, let me spoil the ending: the intrinsic dimensionality of a space is the number of required pieces of information that we need to describe each object in the space. This may differ from the number of pieces of information that we are using, which we call the extrinsic dimensionality of the space.
So what's my recommendation? If you have a text, follow its terminology; perhaps make some mention of this issue, which may stimulate the better thinkers in your class; but try not to let it confuse everyone. That may be hard!
This is advice we give on many topics where perspectives vary.
How about the Möbius strip?
We’ll close with the 2003 question I’d referred to:
Mobius Strips, Spheres, and Dimensionality
Is a Mobius Strip 2-D or 3-D? Or is it 1-D? I find it confusing because we start off with a 2-D strip of paper with a clear height/width. When we twist and join it, we still have a clear width, but we are unsure about length, though you could take this as one circuit of the loop. Depth is very confusing, though, because at one point you have the twist, which seems to have no depth at all. And the rest of it does make a shape which seems 3-D, but the 'depth' of the object is the same bit we measured for the width. Please can you help me? Thanks.
Here is a picture of a Möbius strip:
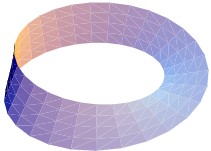
The question is, what are its three dimensions, sometimes called “length, width, and depth”? Or are there only two?
I answered:
Hi, Ruth. Actually, the same questions can be raised about a sphere (meaning the surface, not the solid object we call a ball). It is only a surface, making it 2-dimensional (that is, any point on the surface can be located by only 2 dimensions, such as latitude and longitude). But it is embedded in 3-dimensional space, so that we can also assign each point on the sphere to its (x, y, z) coordinates. The sphere has no thickness (ideally, that is - just as your paper really has some thickness, but we ignore it for the sake of the mathematical concept), so that any small part of it looks like a piece of a plane. Its two-dimensionality depends on that "local" property rather than on the "global" idea of size.
This idea is essentially what we saw earlier about 2-manifolds: it “looks like a plane if you zoom in far enough on it”. And the idea of a “local property” is the source of my idea of “intrinsic” dimension.
Note that the concept of dimensions doesn't really have anything to do with whether the object as a whole has a length, width, and thickness or depth, or whether there is a boundary when you go around it. The sphere has no edges at all, so that within the sphere itself you could only measure how far you go before you loop back on yourself. In the three-dimensional space in which it resides, you can describe it by only one dimension, its radius. But dimensionality relates to how you can specify a location in it, not to the overall size of the object.
And location on a sphere can be specified by latitude and longitude. On a Möbius strip, it could be “distance along” and “distance from the middle”.
Then I referred to the answer we started with, so we’ve come full circle, so to speak.
