(A new question of the week)
Having written last week about the definitions of trigonometric functions, I want to look at a question from a few months ago that illustrates a rather common mistake students make in applying those definitions. It also demonstrates the patience required to find out what is in a student’s mind, and how to correct subtle errors of thinking.
Here is the question:
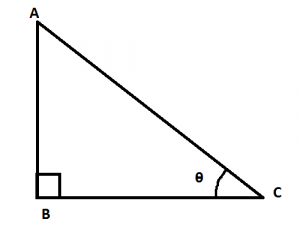
See the triangle in the attachment.
What is cos(B) in the given triangle? Is it BC/CA or AB/CA?
I will be thankful for any help.
There is a fundamental error in the question, so the first thing to do is to find out more about what the student is thinking. The picture is not appropriate for asking about the cosine of B; those are not ratios of sides in this triangle (and in fact, not in any actual triangle). The picture is appropriate for a different question, cos(C). Doctor Jacques gave an initial reply, checking whether the error is just a typo, and answering possible corrected questions:
In your picture, B is a right angle: cos(B) = 0.
If you mean cos(θ) or cos(C), then it is BC/CA.
Note that the subject line of your question is about sin(B). If that is your question, sin(B) = 1 and sin(θ) = AB/AC.
But the student did mean what he had written:
But, I wanted to know the value of cos(B) in terms of the sides of the triangle, i.e., Is cos(B)=BC/AC or cos(B)=AB/AC?
THANKS!
This doesn’t fully clarify what he is thinking, but does confirm that the error is in his thinking, not just his typing. He really wants the cosine of the right angle, and it appears that he recognizes that the denominator of the cosine is the hypotenuse, but doesn’t know which leg to consider “adjacent”, because the picture is not what he is used to.
Now Doctor Jacques can dig a little deeper:
Please check the drawing that you submitted. On that drawing, B is a right angle, and the cosine of a right angle is 0.
In a right triangle, you can express the cosine of an acute angle as a ratio of sides of the triangle (adjacent side / hypotenuse); that does not work for the right angle.
Your drawing has a mark on the angle θ; if you want the cosine of that angle, then it is BC/CA, as I wrote.
He is now pointing out that the drawing does not fit the question asked: a right triangle is the setting for the definition of trig functions of its acute angles, not of the right angle. Now it is the student’s turn to dig deeper:
But, why that does not work for the right angle, and works only for acute angles?
Now we have a good question: What is it about the definition of trig functions that makes this true?
Doctor Jacques explains, by reviewing that definition:
Think about how we would find cos(C). Given the angle C, we construct a right triangle ABC with the right angle at B; we have cos(C) = BC/AC.
Note that the right angle (B) is another angle of the triangle; it is not C itself.
If we want to do that with a right angle, we will get a triangle with two right angles, and that is not possible, as the third angle would be 0.
So, as explained last week, the process of defining the cosine of a given angle C looks like this: We construct the angle; then construct a right angle by making a perpendicular line; and then look at the ratio of sides in the triangle formed:
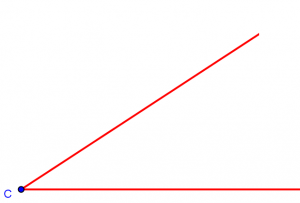
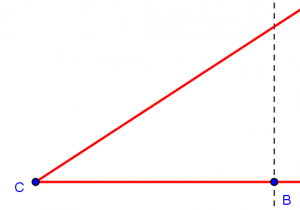
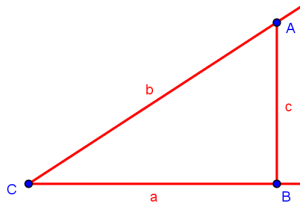
The cosine of our angle C is the ratio a/b.
But if the given angle C were a right angle, we couldn’t make a right angle at B and still have a triangle:

The error underlying the question is probably that the student doesn’t see this process of constructing a triangle from an angle, but pictures taking a right triangle, and any angle in it, as a starting point. If he is interested in a right angle, he may just see the right angle in a traditional picture of a right triangle (as in the attachment to the question above), and look for the “adjacent side” to that angle. (If the question had been about the sine, it would be even more confusing, as the side “opposite” the right angle would have to be the hypotenuse.)
Note the wording of the question: “What is cos(B) in the given triangle?” Trig functions are not relative to a particular triangle; the triangle is constructed from the given angle. How we present the definition of trig functions can be very important, because it is very easy to see the triangle as preexisting when the same picture is used over and over.
So how is the cosine of 90° defined? That is where the extension of the definition, using the unit circle or similar constructions to replace the right triangle, is needed. Here is a picture from our FAQ on Trigonometry Formulas:
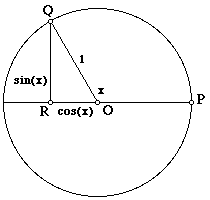
If angle x is 90°, then Q is at the top of the circle, and R is at the origin. The cosine is therefore 0; the “right triangle” is just a line segment.
In case the student is ready for a higher perspective, Doctor Jacques then suggested another way to look at it:
There is another point of view. To find the cosine of the angle between two vectors, we project one of the vectors onto the other (orthogonally). The cosine is the ratio of the projection to the original vector.
If the vectors are perpendicular, the projection is 0, and therefore the cosine is 0.
This orthogonal projection is just what we got when we “dropped a perpendicular” in our construction above:
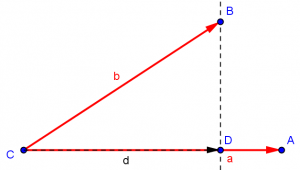
The cosine of angle C is the (signed) length of the projection, d (which you can think of as the “shadow”), of vector b on vector a, divided by the length of b. If b were perpendicular to a, then the projection of b on a would be 0.
The student probably didn’t benefit from this last idea, but thanked Doctor Jacques for the explanation.