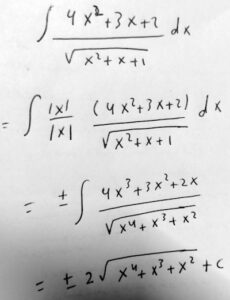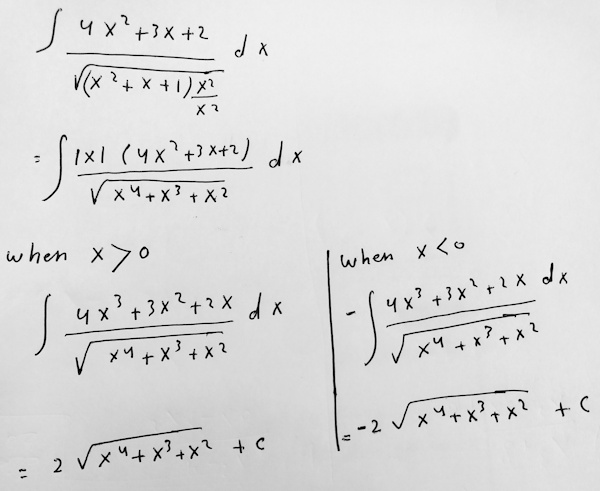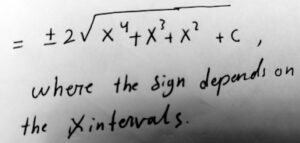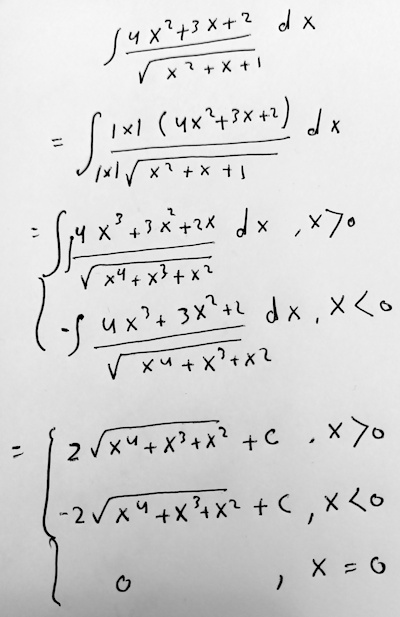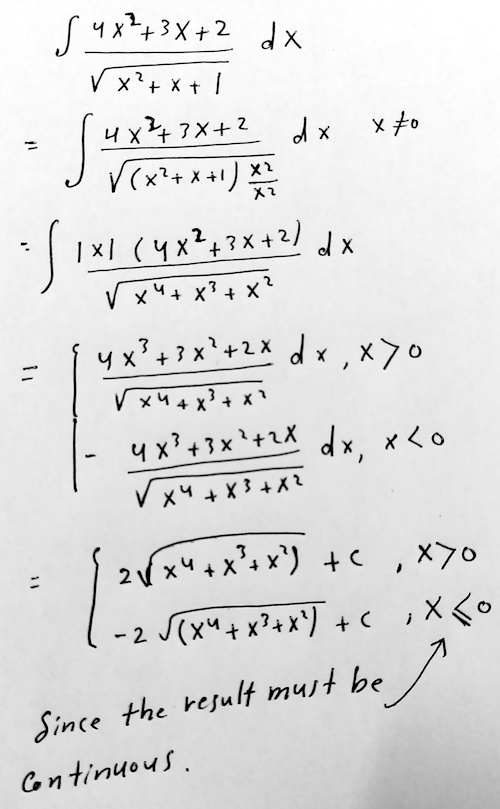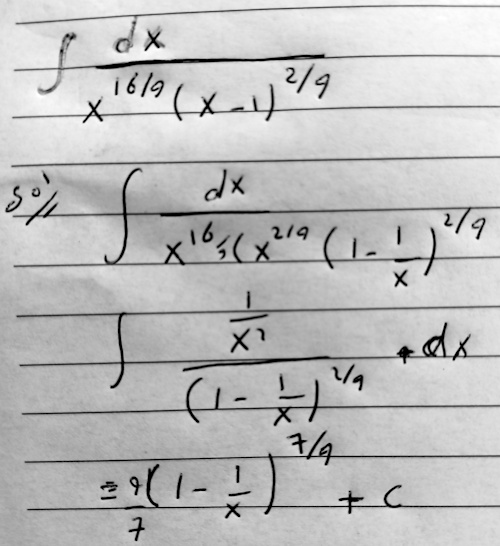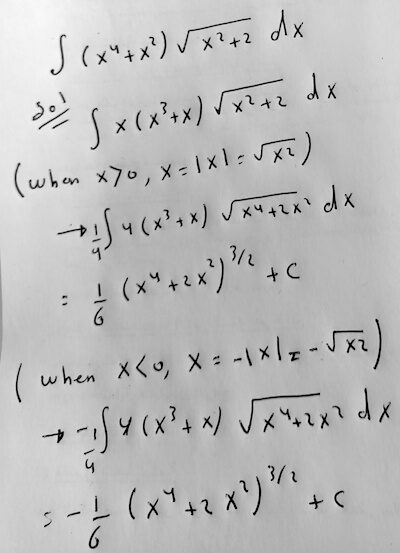Several recent questions involve things that go wrong with signs in integrating, and reveal some subtleties that are easily overlooked. We’ll also see some creative thinking!
Moving x inside a square root
The questions are all from our friend Amia. Here is the first, from late February:
Hi Dr math,
I want to check my solution to the question below.
Amia has multiplied both numerator and denominator by \(|x|\), evidently having seen that this will result in the numerator being the derivative of the radicand, permitting a substitution. When you happen to see something like that, do it! But while the absolute value was needed in the denominator, it made the sign of the numerator uncertain. What to do?
Doctor Rick answered:
Hi, Amia.
Interesting!
The thing that concerns me, just looking at your final answer, is the “±”, which makes this not a function! The idea is good, but something is wrong.
You say you multiplied by 1 in the form |x|/|x|; but actually you multiplied by x in the numerator and |x| in the denominator. You probably thought that the ± would take care of this discrepancy, but as I noted, this introduces a double-valuedness that we don’t want.
The reason for the “±” is that the absolute value is equal to either \(x\) or \(-x\), depending on the sign of x itself. But we have to specify which to use.
How can we do this correctly? Note that x/|x| = sgn(x), the signum function (except at x = 0, where sgn(x) = 0 while x/|x| is undefined — but that’s just a point). So you’re multiplying by sgn(x) essentially, whereas we want to multiply by 1.
To fix this, we could multiply again by sgn(x), since sgn(x)2 = 1 (except, again, at x = 0). That is, we multiply the integrand by sgn(x)x/|x| = 1 (except at 0); the x and |x| are absorbed into the integrand as you did, leaving sgn(x) multiplying the quantity that you integrated.
I would have to think more deeply than I can at the moment to justify pulling the sgn(x) out of the integral.
The signum function is defined as $$\text{sgn}(x)=\left\{\begin{matrix}
-1&\text{if }x<0 \\0&\text{if }x=0\\1&\text{if }x>0\\\end{matrix}\right.$$
The fact that it is equal to \(\frac{x}{|x|}\) except at one point is related to a point we noted last time (no pun intended!), that changing the integrand at one point (even an endpoint) has no effect on the integral.
The reason we actually can pull that signum function outside of the integral, replacing the “±” with \(\text{sgn}(x)\) even though it is a function of x, is that it is just a (piecewise) constant function, always equal to 1 or -1.
However, when I take my result,
F(x) = 2 sgn(x) √(x4 + x3 + x2) + C
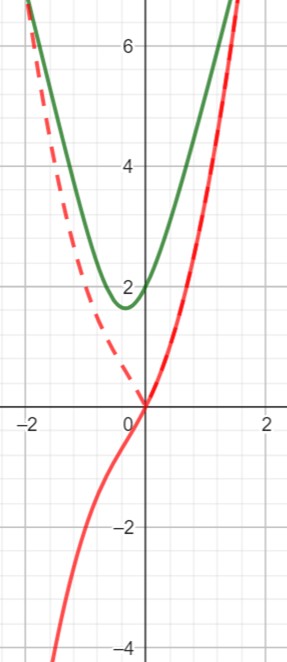
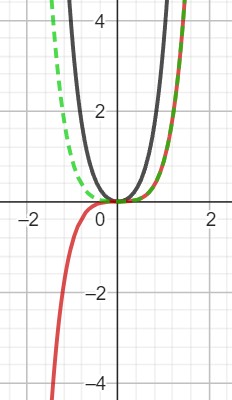
and differentiate it, I do get the original function back. Here is a graph:
The green curve is the original function (integrand), and the red curve is the antiderivative F(x) with C = 0. Without the sgn(x) in F(x), that function would follow the dashed line. (Its derivative is not the original function.)
Amia suggested a slightly different approach:
Thank you Dr Rick.
So I can accept it like the solution below?
Here the two cases have been dealt with separately, keeping the answer in piecewise form. It also raises more explicitly the question, what should the antiderivative be when \(x=0\)? Since the integrand is not defined there, that is a moot question; but by filling in the hole, letting \(F(0)=0\), we make it equivalent to the sgn form, and make a function that is, in fact, everywhere differentiable.
Doctor Rick responded:
Yes, I think that is a perfectly reasonable way to do it, avoiding the complication that I introduced with sgn(x).
Amia suggested an alternative to the final answer:
I think I saw the answer below in similar situations.
Doctor Rick answered:
This answer is, of course, incomplete; we need to say precisely what that dependence is. Your last solution did this: the sign is + for x > 0 and – for x < 0.
Amia went further:
This solution?
Doctor Rick replied:
I wondered if you might eventually raise the issue of what happens at x = 0, which I had deliberately glossed over.
Since the integrand is defined for all x, the indefinite integral should be differentiable for all x. In order to make it continuous (a requirement for differentiability), we need to change what you wrote above to “C, x = 0”. This was probably just an oversight on your part.
Now, since √(x4 + x3 + x2) = 0 for x = 0, we can simply drop the third line above and change “x > 0” to “x ≥ 0”.
Amia made some small changes:
Here final answer.
Doctor Rick concluded:
My first reaction was that we could make the solution simpler by using |x| = {x, x ≥ 0; –x, x < 0} to write the piecewise form with x ≥ 0 instead of x > 0, and thus not need your last step (involving continuity). But then I remembered that in the first step we multiply by x2/x2, with the result that the modified integrand is undefined for x = 0. It’s a removable discontinuity, but the way to resolve it is just what you did. I don’t think I could improve on it.
(Except that you omitted integral signs in the piecewise step.)
It would be nice to have a simpler form for the answer; how about applying the same trick we used to carry out the integration? We can rewrite \(2\sqrt{x^4+x^3+x^2}\) as \(2\sqrt{x^2(x^2+x+1)}=2|x|\sqrt{x^2+x+1}\), and now if we multiply this by sgn(x), we get \(2x\sqrt{x^2+x+1}\) as our antiderivative. And in fact, its derivative is our integrand:
$$\frac{d}{dx}2x\sqrt{x^2+x+1}=[2]\left[\sqrt{x^2+x+1}\right]+[2x]\left[\frac{2x+1}{2\sqrt{x^2+x+1}}\right]\\=\frac{2(x^2+x+1)+x(2x+1)}{\sqrt{x^2+x+1}}=\frac{2x^2+2x+2+2x^2+x}{\sqrt{x^2+x+1}}\\=\frac{4x^2+3x+2}{\sqrt{x^2+x+1}}$$
We’ll see something similar later.
On the other hand, there are probably several other ways to solve this integral, which likely bypass the sign issue entirely, though they may take a little more work. We didn’t pursue that.
Similar work with a ninth root
The next question is from mid-March, with a similar procedure involving ninth roots:
Hi Dr math,
I want to check if the solution is complete?
Is there any need to use absolute value when I took the common factor x^2/9?
Here he multiplied and divided the denominator by \(x^{2/9}\), again obtaining a new numerator that is the derivative of the inner function, allowing for a substitution, \(u=1-\frac{1}{x}\). The similarity probably triggered a concern.
I answered:
I see no place where I would consider using an absolute value.
If you were factoring something out of a square root, you would need to consider that; but here we have an odd root (9th), so that is not an issue; and that is squared (2/9 exponent), which would make x2/9 positive anyway!
The work looks good. And it’s good that you do consider issues like this, which are easy to miss when they do matter!
I checked with Wolfram Alpha just to make sure:
So odd roots don’t cause sign trouble.
Three more integrals
Here is the last of the series, from a couple days later:
Hi Dr math ,
I have the three integrals below ,and I want your opinion.
This was followed by three images. I’ll show each of them as we answer it below.
1. Another radical with a hidden sign issue
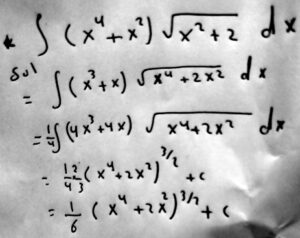
I answered:
Do you have any specific questions about these?
For the first, your method is nice; I suppose you saw that a little manipulation happens to give a u and a du. I haven’t tried other ways, to see how much effort you save this way.
I would often be very interested in seeing a description of your thinking, which could be worth sharing with others.
The work is similar to our first problem above; we’ll see it again soon, for similar reasons! Do you notice how he quietly moved an x inside the radical? I didn’t (yet)!
But let’s try working it out in a more routine way.
Not seeing anything else to do, I might let \(u=x^2+2\), the radicand, so that \(du=2xdx\), and \(x=\sqrt{u-2}\) … but that assumes \(x\ge0\), bringing in our sign issues. I’ll just assume \(x\ge0\) for now!
We get $$\int(x^4+x^2)\sqrt{x^2+2}dx=\int(((u-2)^2+(u-2))\sqrt{u}\frac{du}{2\sqrt{u-2}}\\=\int\frac{(u-2)(u-1)}{2\sqrt{u-2}}\sqrt{u}du=\int\frac{1}{2}(u-1)\sqrt{u-2}\sqrt{u}du\\=\frac{1}{2}\int(u-1)\sqrt{u^2-2u}du$$
Now we have a new radicand, and might try that as a substitution: Let \(v=u^2-2u\), so that \(dv=2u-2=2(u-1)du\). Things look surprisingly nice; we get $$\frac{1}{2}\int(u-1)\sqrt{u^2-2u}du=\frac{1}{4}\int\sqrt{v}dv\\=\frac{1}{4}\frac{2}{3}v^{3/2}=\frac{1}{6}(u^2-2u)^{3/2}\\=\frac{1}{6}(u(u-2))^{3/2}=\frac{1}{6}((x^2+2)(x^2))^{3/2}\\=\frac{1}{6}(x^4+2x^2)^{3/2}$$
which looks familiar. Our two substitutions amount to \(v=u^2-2u=u(u-2)=(x^2+2)(x^2)=x^4+2x^2\), which is exactly what Amia did all at once.
2. Shortcuts for a trig integral
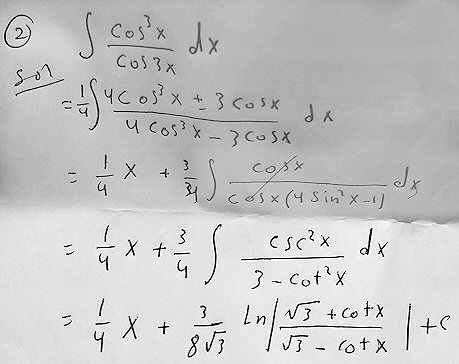
I didn’t follow what you are doing in the first step:
$$\int\frac{\cos^3x}{\cos3x}dx=\frac{1}{4}\int\frac{4\cos^2x\pm3\cos x}{4\cos^3x-3\cos x}dx$$
From the next line, I suspect you intended the numerator there to be 4cos3x – 3cos x + 3cos x (which is not the same as what you wrote). This is what I have sometimes called ‘partial cancellation”, and have compared to long division. I might instead have substituted u = cos x and used long division on the resulting u3/(4u3 – 3u).
I introduced my term “partial cancellation” in Integrating Rational Functions: Beyond Partial Fractions, and saw it again in Integration: It Takes a Whole Toolbox.
If I’m right, then his work, in more detail, would start like this:
$$\int\frac{\cos^3(x)}{\cos(3x)}dx=\frac{1}{4}\int\frac{4\cos^3(x)}{4\cos^3(x)-3\cos(x)}dx\\=\frac{1}{4}\int\frac{4\cos^3(x)-3\cos(x)+3\cos(x)}{4\cos^3(x)-3\cos(x)}dx\\=\frac{1}{4}\int\left(\frac{4\cos^3(x)-3\cos(x)}{4\cos^3(x)-3\cos(x)}+\frac{3\cos(x)}{4\cos^3(x)-3\cos(x)}\right)dx\\=\frac{1}{4}\int1dx+\frac{1}{4}\int\frac{3\cos(x)}{(4\cos^2(x)-3)\cos(x)}dx\\=\frac{1}{4}x+\frac{3}{4}\int\frac{1}{4\cos^2(x)-3}dx$$
The third line in his work makes an unexplained leap from this.
But there are more places where I don’t follow your work, and am not sure it is correct. And your final answer could be rewritten in various ways to make it easier to compare with results obtained by other methods
Can you show more steps and explanation?
He didn’t show more.
Here is my best guess at the rest, with corrections: $$=\frac{1}{4}x+\frac{3}{4}\int\frac{dx}{\cos^2(x)+3(\cos^2(x)-1)}\\=\frac{1}{4}x+\frac{3}{4}\int\frac{dx}{\cos^2(x)-3\sin^2(x)}\\=\frac{1}{4}x+\frac{3}{4}\int\frac{dx/\sin^2(x)}{\cos^2(x)/\sin^2(x)-3\sin^2(x)/\sin^2(x)}\\=\frac{1}{4}x+\frac{3}{4}\int\frac{\csc^2(x)dx}{\cot^2(x)-3}$$
This is his fourth line, but with a difference in sign.
Now we substitute \(u=\cot(x)\), \(du=-\csc^2(x)dx\), and then use partial fractions:
$$\int\frac{\csc^2(x)dx}{\cot^2(x)-3}=\int\frac{-du}{u^2-3}\\=\int\frac{du}{3-u^2}=\int\frac{du}{(\sqrt{3}+u)(\sqrt{3}-u)}\\=\frac{1}{2\sqrt{3}}\int\left(\frac{1}{\sqrt{3}+u}+\frac{1}{\sqrt{3}-u}\right)du\\=\frac{1}{2\sqrt{3}}
\left(\ln\left|\sqrt{3}+u\right|-\ln\left|\sqrt{3}-u\right|\right)du\\=\frac{\sqrt{3}}{6}\ln\left|\frac{\sqrt{3}+u}{\sqrt{3}-u}\right|=\frac{\sqrt{3}}{6}\ln\left|\frac{\sqrt{3}+\cot(x)}{\sqrt{3}-\cot(x)}\right|$$
So our final result is $$\frac{1}{4}x+\frac{3}{4}\frac{\sqrt{3}}{6}\ln\left|\frac{\sqrt{3}+\cot(x)}{\sqrt{3}-\cot(x)}\right|=\frac{1}{4}x+\frac{\sqrt{3}}{8}\ln\left|\frac{\sqrt{3}+\cot(x)}{\sqrt{3}-\cot(x)}\right|$$
which is what Amia got.
Wolfram Alpha gives a different-looking answer that requires some work to see that it is equivalent:
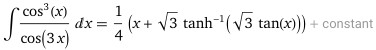
3. Another radical, using parts and a specialized trick

The answer and the work are both good. The trick you use at III is unexpected, but is equivalent to the trick I had to use after substituting x = tanθ, leading to ∫secθdθ, which one either memorizes or learns the trick (multiply by (secθ + tanθ)/(secθ + tanθ)). I made that substitution from the start, but your way is very nice, and possibly better.
We didn’t dig into this one, so I won’t try to elaborate. The trick used here is related to methods shown in Integration: More Than One Way, More Than One Answer.
Back to the sign issue!
Doctor Rick pointed out a connection from the first of these three, to our first question in this post:
Your work on problem 1 reminds me of a problem that you and I discussed recently, so I’d want to check that it doesn’t have the same issue.
$$\int(x^4+x^2)\sqrt{x^2+2}dx=\int(x^3+x)\sqrt{x^4+2x^2}dx\\=\frac{1}{4}\int(4x^3+4x)\sqrt{x^4+2x^2}dx=\frac{1}{4}\frac{2}{3}(x^4+2x^2)^{3/2}\\=\frac{1}{6}(x^4+2x^2)^{3/2}+C$$
I notice that your solution is positive everywhere except at x = 0, where it is zero. Thus its derivative (the integrand) ought to be negative to the left of 0, but in fact it is positive everywhere. Something is evidently wrong with your solution, and I suspect it’s the same sort of issue we discussed. I haven’t looked at it in detail yet; I’ll give you a shot at it first.
This is a useful way to check an integral.
To confirm my suspicions and show the resemblance to the issue from that other problem, here is a graph; the integrand is in black, your solution is the green dashed line, and GeoGebra’s solution is in red.
Using technology (in this case GeoGebra’s ability to integrate numerically) is another good way to check! We can see that the correct answer needs a sgn(x), just as before.
I saw how I’d missed this issue, which is instructive:
Before saying you were correct, I had checked with Wolfram Alpha, which gave this:
I failed to notice that although at first glance this agrees with your answer, 1/6 (x4 + 2x2)3/2, it will have the same sign as x, whereas yours is always positive! That’s because (x2)3/2 ≠ x3.
That issue arises on the very first line of your work, where you implicitly assume that x = √(x2).
And I thought I had given myself enough time to be right. (Technically, I suppose, I didn’t actually say your answer was correct …)
It’s the same error we saw before, but in a very slightly different form.
Amia responded:
I made a new solution:
I responded:
Yes, a piecewise solution is the easiest way to correct for the sign error. What you write looks valid.
Alternatively, you could combine the two cases by writing
x = sgn(x)√(x2),
which is true for all x (positive, negative, or zero), leading to the solution
sgn(x)/6 (x4 + 2x2)3/2
Then you could factor out x2 to get
1/6 x3 (x2 + 2x)3/2
by observing that (x2)3/2 = x3 sgn(x), and the signs cancel.
This is one way to obtain Wolfram Alpha’s solution.
I’ve tried looking for an approach that would not require separately checking signs, but always ran into a similar issue.
So we don’t need a piecewise function, or the sgn function, in our final answer. But we do have to pay close attention to signs as we work.
Readers are invited to suggest alternate methods for any of the integrals shown here.