Ranking a Word Among Its Permutations

(A new question of the week)

There are some topics that appear to be standard in certain parts of the world, but far less familiar in our own. Sometimes it takes two of us to recognize what a student is asking, due to language issues and different past experience with such questions. This is an example that gets into a couple challenging areas of combinatorics.

Two problems

Kurisada asked this in March:

There are 8 letters: A, B, H, N, O, S, U, U

1. If I take 6 numbers from above, how many possible arrangements can be made?

2. If I arranged the letters into the word “OUBUNSHA”, what is the number of order of the word? (I don’t know how to say this in English, but I mean: ABHNOSUU is the first order and the total order is 8!/2!)

The second question at first glance appeared to be one we had previously discussed (see last week’s post, Arranging Letters with Duplicates); the first is trickier. Doctor Rick took the question:

Based on our previous discussion, I figure you would have no trouble with problem 2. Is there anything you want to ask us about that? (Besides how to state the question — I might say: In how many ways can the letters of OUBUNSHA be arranged (or permuted, or ordered)?)

Regarding problem 1, I would consider two cases separately:

1. The six letters selected are all different, that is, selected from {A, B, H, N, O, S, U}

2. The six letters include both U’s and four more chosen from {A, B, H, N, O, S}

He has interpreted “What is the number of order?” as “How many orderings are there?” That makes sense, but will turn out to be wrong; in fact, Kurisada has answered that question, calling it the “total order” (total number of permutations). We’ll get to that in a moment.

Breaking a problem into cases sometimes feels like cheating, because it can verge on “brute force”, and sometimes there are ways to avoid it; but it is often the best way. Here there are only two cases to consider, so it is a reasonable strategy.

Rank of a word

Before Kurisada answered, I jumped with a suggested interpretation of problem 2, having seen something like it in the Ask Dr. Math archives:

If I may add one comment, I am wondering if the second question might be asking for the “rank” of a word, as discussed here:

Rank of the Word FOCUS

That is the word’s “order” (position) within an alphabetized list of all possible “words”.

This fits with Kurisada’s identification of ABHNOSUU as the first permutation (“order”) of the letters; he is asking for the position (“number”) of the given word OUBUNSHA in this sorted list of permutations (“orders”). Mathematical words can be very tricky for someone translating an unfamiliar problem into English; the word choice is often almost arbitrary, as “order” and “rank” are almost synonymous in ordinary English.

Doctor Rick now responded:

I think Doctor Peterson has the right idea about what you were trying to say. When you said, “ABHNOSUU is the first order and the total order is 8!/2!”, you were trying to say that of all the words formed by permutation of these letters, ABHNOSUU is the first word in alphabetical order, and that the total number of words is 8!/2!. I had thought you were just asking about that total number, which is what we had discussed in regard to the previous problem.

The archived answer to which Doctor Peterson pointed you is pretty easy to follow. I’m glad he thought of this!

Let’s look at that archive page. Here is the question, from 2003:

Rank of the Word FOCUS

The letters "CFOSU" are arranged in dictionary order. What is the rank of the word "FOCUS" in this order?

Thank you a lot in anticipation.

Note that the question is not written clearly; it should really say that all permutations of CFOSU are listed in order, not the letters themselves (which are, in fact, in order as written). But the correct word, rank, was used in the problem, which made it clear enough to those who recognize the term in this context.

Doctor Achilles answered, first stating the problem clearly, and then changing the representation to make it easier to see the ordering:

Let's use a code to solve this problem. We have the following letters:

  C

  F

  O

  S

  U

And we will take all the permutations of these letters and arrange them in alphabetical order.

I think it will be helpful to think of these letters as numbers. The first letter, alphabetically, in this list is C, so let's replace "C" with the number 1.

The second letter is F, so let's replace it with 2.

And so on.

Using this code, the word "FOCUS" will be the sequence:

  2 3 1 5 4

The first permutation in the sequence "alphabetically" is:

  1 2 3 4 5

Then

  1 2 3 5 4

Then

  1 2 4 3 5

And it goes on like that.

Now alphabetical ordering is replaced with ordinary numerical ordering. Our list of permutations will start out as:

• 12345
• 12354
• 12435
• 12453
• 12534
• 12543
• …
• 23154 (FOCUS)
• …
• 54321

This list contains \(5! = 120\) entries. Where is our number in the list? We won’t find a mere formula, but there is an algorithm – an orderly procedure we can follow.

The permutation we want is, again:

  2 3 1 5 4

Which starts with a 2, so it comes AFTER every permutation that starts with a 1. How many permutations start with a 1? The answer to that is the number of ways the digits:

  2 3 4 5

can be arranged. A quick look at our FAQ on permutations

   Permutations and Combinations
   http://www.mathforum.com/dr.math/faq/faq.comb.perm.html 

tells us that that number of combinations is going to be 4! (4*3*2*1) or 24.

So our list consists of 24 numbers starting with 1, then 24 more starting with 2, among which is the number we are “focusing” on.

So there are 24 permutations that begin with 1. That means that the 25th permutation is:

  2 1 3 4 5

Now we've gotten the first digit in place. The next digit we want is 3. So we are going to have to work through all of the permutations that start with "2 1". How many are there?  3! (3*2*1) or 6.

So the 31st permutation is:

  2 3 1 4 5

And the 32nd permutation is:

  2 3 1 5 4

Which is the one we wanted.

After 24 starting with 1, we have 6 starting with 21. There are none starting with 22 (don’t be fooled!); our number is the second one starting with 23. So it is number 24 + 6 + 2 = 32. For confirmation, here is the list up to that point:

1. 12345
2. 12354
3. 12435
4. 12453
5. 12534
6. 12543
7. 13245
8. 13254
9. 13425
10. 13452
11. 13524
12. 13542
13. 14235
14. 14253
15. 14325
16. 14352
17. 14523
18. 14532
19. 15234
20. 15243
21. 15324
22. 15342
23. 15423
24. 15432
25. 21345
26. 21354
27. 21435
28. 21453
29. 21534
30. 21543
31. 23145
32. 23154

So the steps to solving this are:

1) Assign a number to each letter using alphabetical order.

2) Determine what number sequence corresponds to the word you want.

3) Determine how many permutations it takes to get the first letter into place.

4) Now that the first letter is set, focus on the remaining letters and repeat step 3 until you're done.

We could probably turn this into something close to a formula if we were going to be doing this a lot; but for most of us, practicing the orderly thinking involved is more important than devising a formula or writing a program to do it.

Our problem will be considerably harder than this example!

Permutations of 6 letters from ABHNOSUU

Back to our discussion, Kurisada confirmed our interpretation of problem 2, then solved problem 1:

Thank You Doctor for the link!

And yes Doctor, for number 2, I meant the rank of the word.

Then, here are what I tried:

1. I separate it into 2 parts as Doctor said

The first one, I made 7P6 = 7!/1! = 5640 (In these arrangements, the arranged word may take no U or 1 U).

The second one, I made 6P4 = 6!/2! = 360 (the arranged word takes 2 U).

So the total is 6000.

I’ll look at his answer for problem 2 below, after we finish this one.

Recall that the first case is when the six letters chosen are all different; we are just permuting 6 letters from ABHNOSU. The second case is when two letters are the same, namely UU, so we are choosing 4 from ABHNOS, and then mixing in UU with them. Kurisada has so far only chosen the other 4 letters.

Before any response, Kurisada made a correction:

Now I think my number one for 2 U is wrong, because it hasn’t included the Us yet.

So I find the number of arrangements:

a. If the Us are adjacent to each other (I made it to X)

__ A __ B __ H __ N __

There are five places to input X

b. If the Us are separated

__ A __ B __ H __ N __

I made = 5! / (3! 2!) = 10

So there is 15 arrangements for U

And the total arrangements for the second part is 15 x 360 = 5400.

And the total arrangements (first and second part combined) is 11040.

If we want the UU together, we have to choose one of 5 places to put it, so we multiply the \(_6P_4\) ways to place the non-U’s by 5 ways to place the UU.

If we want UU separate, we have to choose two of the 5 places to put them, so we multiply this time by \(_5C_2\).

Doctor Rick replied:

Your revised answer isn’t what I got, but I think that is due to a simple miscopying of a number: 7! = 5040, not 5640. (You wrote this correctly on problem 2.) With this one correction, your answer will be 10440.

I used a different approach to get the same answer for the number of words with two U’s. First I select four of the 6 non-U letters (ABHNOS): 6C4 = 6!/(4! 2!) = 6*5/2 = 15. Then I permute the six letters including the two U’s, which can be done in 6!/2! ways. The result is 15*6*5*4*3 = 5400.

We really like it when we can get the same result for a counting problem in two ways, because it’s hard to be really confident that we haven’t missed something or else overcounted.

Instead of splitting the arrangements according to whether the U’s are together as Kurisada did, Doctor Rick first chooses (without arranging) the 4 other letters, in 15 ways, and then permutes all 6 letters, 2 of which are alike, in \(\frac{6!}{2!} = 360\) ways. We previously explored this in Arranging Letters with Duplicates.

Rank of OUBUNSHA

Now we can look at problem 2, the rank question. It will help in reading this to see that Kurisada has changed ABHNOSUU to the numerical form 12345678, so that OUBUNSHA becomes the number 57284631. This ignores the two U’s, so I’d consider it a good practice run before solving the actual problem – not a bad idea! We should really be looking for the position of 57274631 among all permutations of 12345677.

Apart from this, his work is very good (and even clearly written, considering how much has to be said).

But here is his work:

2.

The number of arrangements when the first digit is 1 is 7! = 5040

And it’s the same for 2, 3, and 4

So when the first digit is 1/2/3/4, the number of arrangements is 20160

Then the next arrangement has the first digit of 5 (I don’t add 1 here, but I’ll add it below)

When the second digit is 1, the number of arrangements is 720

When the second digit is 1 – 6 except 5 (because 5 has been taken), the number of arrangements is 3600

The next arrangement is 57123468

When the third digit is 1, the number of arrangements is 120

The next arrangement is 57213468

When the fourth digit is 1, the number of arrangements is 24

When the fourth digit is 1/3/4/6/8, the number of arrangements is 96

The next arrangement is 57281346

When the fifth digit is 1, the number of arrangements is 6

When the fifth digit is 1/3, the number of arrangements is 12

The next arrangement is 57284136

When the sixth digit is 1, the number of arrangements is 2

When the sixth digit is 1/3, the number of arrangements is 4

The next arrangement is 57284613

And the next arrangement is 57284631

So the rank is 20160 + 3600 + 120 + 96 + 12 + 4 + 1 + 1 = 23994

Wow the way is very long! (But I fully understand this concept)

I wonder if there is a more simple way

Doctor Rick replied to this:

You left out some helpful information on your method at the start. I suppose that you took the advice in the Ask Dr. Math answer and changed the word into a number. However, the example was simpler than yours because it had no repeated letters. Also, of course, the word is longer! I assume that these factors are what made it so complicated. Let me just try it myself and see how it goes.

I will stick with letters. The letters to be permuted are ABHNOSUU. We first need to find the number of words preceding OABHNSUU (the first word starting with O). We count the words beginning with A: this requires permuting the letters BHNOSUU, which can be done in 7!/2 ways. We will get the same count for words beginning with B, H, and N, so the total number of words preceding OABHNSUU is 4×7!/2 = 10,080.

Hmm … that’s already different from your answer. I suppose you forgot to take into account that the two U’s are identical?

At this point I drop the O; we consider the word UBUNSHA. We want to find the number of words beginning with A, B, H, N. or S among the permutations of ABHNSUU. Following the same procedure I obtain 5×6!/2 = 1800 words preceding UBAHNSU.

Dropping the first U, we now consider the word BUNSHA, finding the number of words beginning with A among the permutations of ABHNSU. All the letters are distinct now, so the next number is 1×5! = 120.

It appears that starting from this point I’m going to get the same answers you got, because the problem of having two identical letters is out of the way. But it certainly is tedious! This is all new to me, so others may already know a quicker way, but I don’t; so let’s look at the series I’ve found thus far:

4×7!/2 + 5×6!/2 + 1×5! + …

If we want to find a quicker way, I think it will involve defining exactly how to determine each factor in each term, so that we don’t need to think as much in the future. The first factor is the tricky one. I’m not going to do more work on this, at least at present (as I must leave soon). Perhaps another Math Doctor will either know a way, or find a resource with further help.

Kurisada answered,

Thank You very much Doctor!

And yes I forgot if there are 2 Us

I have no more experience with this than Doctor Rick, but I had time to search for a resource:

I have seen only a couple questions of this type in the past, but they made it clear that this is a topic explicitly taught in some curricula. Searching for more information just now, I found this page that explains a routine procedure, and will even solve your problem for you:

https://www.careerbless.com/calculators/rank/index.php .

It gives the answer as 12114.

Here is the output of that rank calculator for our problem:

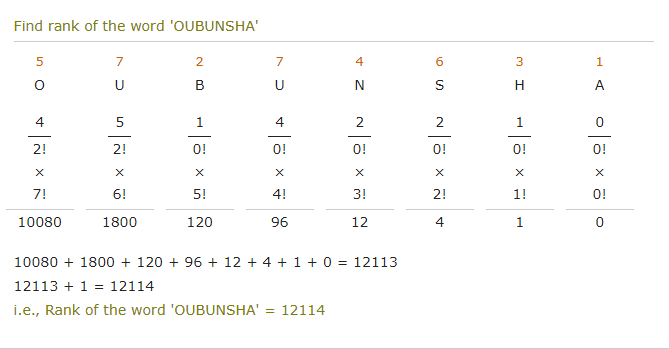
The fractions in the third row consist of the number of lower values to the right of each place, over the number of ways to arrange the duplicate letters. These are multiplied by the number of ways to permute the letters to the right, and then added. All the work and the results agree with what Doctor Rick obtained, as well as much of Kurisada’s.