(A new question of the week)
Let’s look at a quick question from mid-September, that had a number of different answers. In some ways, this is an easy question; but we’ll take it a little further, so keep reading to the end.
Can I multiply a fraction and a decimal?
Azraf asked:
Can I multiply a fraction with a decimal number?
We are regularly taught how to multiply two fractions, and how to multiply two decimals; but what happens when you combine them? An example would have been helpful, to make sure we dealt with the kind of problem Azraf is dealing with, but the question is reasonably clear, apart from the fact that it is probably not intended to be taken literally as a yes/no question! The big question is, how? And, perhaps, is there a specific method to do such a multiplication directly?
Three ways
I answered, choosing a simple example to start with:
Hi, Azraf.
Quick answer: yes. Fractions and decimals are both numbers, so they can be multiplied.
Long answer: I’ll want to see what you are thinking when you ask the question. Possibly what you are really asking is something like this: Can I multiply a fraction and a decimal number without first converting one to the other form?
For example, we can multiply 1/3 × 0.75 by converting 1/3 to the (approximate) decimal 0.3333 and multiplying to get 0.249975, which rounds to 0.25.
Or, we can do it by converting 0.75 to the fraction 3/4, then multiplying 1/3 × 3/4 = 1/4. This answer is exact.
But we don’t have to explicitly convert. Instead, we can just divide 0.75 by 3 to get 0.25 (again exact). Here we didn’t convert anything, but used rules for working with fractions. We can think of this as rewriting 1/3 × 0.75 as the fraction 0.75/3 and simplifying by dividing.
There are several other ways I can think of doing it.
I’d love to hear what you had in mind specifically, so we can discuss your thoughts.
My first suggested method does the multiplication in decimal form: $$\frac{1}{3}\times 0.75 = 0.333…\times 0.75 = 0.249975…\approx 0.25$$ This gives the impression that the answer is not necessarily accurate; and it requires some long and tiring work if you want to multiply by hand. (If you use this method on a calculator, you would just treat the fraction as a division, which will automatically be done as decimals: \(1\div 3\times 0.75 = 0.25\). Doing it this way, the calculator isn’t rounding, and will get the answer more accurately than we did by hand.)
My second method does the multiplication in fractional form: $$\frac{1}{3}\times 0.75 = \frac{1}{3}\times \frac{3}{4} = \frac{1\times 3}{3\times 4} = \frac{1}{4}$$ This makes is clear that our answer is in fact exact. If we do this by hand, the hard part is in converting the decimal to a fraction, by long division (though in this case, you might well just recognize it). Then we have to simplify the answer. But it is reasonably straightforward. (Using a calculator, you would have to be able to convert a decimal to a fraction; my TI-30X IIS does this for 0.75, using the “F◄►D” button, but it doesn’t work for uglier decimals like 0.7557.)
My third suggestion uses fraction methods with the decimal just as we would multiply the fraction \(\frac{1}{3}\) by the integer 75: $$\frac{1}{3}\times 0.75 = \frac{1}{3}\times \frac{0.75}{1} = \frac{1\times 0.75}{3\times 1} = \frac{0.75}{3} = 0.25$$
The specific problem
Now, as hoped, Azraf provided a specific example; as I expected, it was a little more complicated than my intentionally simple one, but not by a lot:
I want to do this calculation: 110/100×694.44. I am struggling to do it.
While I was busy that morning, Doctor Rick took an interest and responded:
Hi, Azraf. Doctor Peterson will probably have his own thoughts to share with you, but for now let me point out that all three methods that he mentioned can be applied to your expression:
110/100 × 694.44
First, we could convert the fraction 110/100 to a decimal; this is particularly easy because of its denominator. Can you do this, then complete the multiplication?
Second, we could convert the decimal 694.44 to a fraction. This is the reverse of the process you’d use to convert 110/100 to a decimal; in fact, we’ll end up with the same denominator, 100.
Third, we can use the rules for working with fractions. How would you multiply 110/100 by the whole number 694? You should be able to do exactly the same thing with 694.44 in place of 694; if you can’t figure out how, show us the steps you’d use and we can help.
In fact, it will be helpful if you can try all three methods, and show us your work. That will give us more to talk about, and a better idea of where you are struggling.
Let’s apply the three methods, as I did above:
As decimals: $$\frac{110}{100}\times 694.44 = 1.10\times 694.44 = 763.884$$ Since the decimal terminated (as division by 100 always will), this is an exact answer despite working in decimals.
As fractions: $$\frac{110}{100}\times 694.44 = \frac{110}{100}\times \frac{69444}{100} = \frac{110\times 69444}{100\times 100} = \frac{7638840}{10000} = \frac{190971}{250}$$ If we want a decimal answer, we can just divide and get the same answer as before; but working in fractions suggests we want a fractional answer, and that means simplifying. Not so easy without the fraction button on your calculator!
Combined: $$\frac{110}{100}\times 694.44 = \frac{110}{100}\times \frac{694.44}{1} = \frac{110\times 694.44}{100\times 1} = \frac{76388.4}{100} = 763.884$$
I’d seen the response and given it some thought, but when I had time to respond, I found I had nothing to add:
Doctor Rick said exactly what I was going to say, so it must be good advice!
I look forward to seeing your work, whether you are now able to do it successfully or not, as there may be more to discuss.
Azraf responded with some work:
Is it correct? After trying a lot, I came to this stage. If wrong, please describe it.
Clearly this is correct; Azraf used my third method, with some simplification before actually multiplying, first canceling a 10, and then dividing to get a decimal.
I responded with approval, plus demonstrations of the other methods:
Yes, that is correct. Good work!
If you converted the fraction to a decimal, the work would be very similar. Since 110/100 = 1.1, you would multiply 1.1 × 694.44; in doing that by hand, you would multiply 11 × 69444 to get 763884, and then divide by 1000 (move the decimal point three places) to get 763.884.
And if you converted 694.44 to a fraction, you would be multiplying 110/100 × 69444/100, so the numerator would be 110 × 69444 = 7638840, and the denominator would be 10000. Everything looks very similar.
Azraf closed:
Thanks for help. Will discuss again mathematical problems in near future.
Stay safe.
Azraf
An old example
But let’s not stop there. Azraf’s problem was particularly easy by all three methods, because the denominator was such as to make the fraction almost a decimal. Shall we do a couple more examples?
In writing up this post, I found only one question like this in the Ask Dr. Math archive, from 1996:
Multiplying a Fraction by a Decimal How do I simplify and multiply: 40 ----- x 78.5 360
Doctor Mike answered:
Hi Glenn,
There are several ways to do this. If you have a calculator, you could do 40/360 first, and then multiply that by 78.5 .
If you are doing it by hand, then the easiest way is to first reduce the fraction to lowest terms. The numerator 40 and the denominator 360 are both multiples of 10, so you could divide both numerator and denominator by 10 to get the equivalent fraction 4/36 . Since 4 times 9 is 36, this fraction is equivalent to 1/9 .
Your original problem is now
1
--- x 78.5
9
That is the same as 78.5/9 which you can do on paper with long division. Either way the answer is an infinitely repeating decimal 8.722222222... . A good approximate value is 8.722.
So he first gave what amounts to the decimal approach, just doing the division and getting a decimal result: $$\frac{40}{360}\times 78.5 = 0.111…\times 78.5 = 8.7222…$$ I did this on my calculator without writing down and retyping the intermediate result, so that there was no rounding involved (except at the far end of the calculator’s memory). This is probably how it would usually be done in the real world.
Then he did what amounts to my mixed method, first simplifying the fraction (which I would only do if it was easy, as this one is) and then treating the resulting fraction as a division: $$\frac{40}{360}\times 78.5 = \frac{1}{9}\times 78.5 = 78.5\div 9 = 8.7222…$$
If we had some reason to want a fractional result, we might use my pure fraction method, multiplying \(\frac{1}{9}\times 78\frac{1}{2}\). Recall that we do such a multiplication by writing the mixed number as an improper fraction: $$\frac{40}{360}\times 78.5 = \frac{1}{9}\times 78\frac{1}{2} = \frac{1}{9}\times \frac{157}{2} = \frac{157}{18} = 8\frac{13}{18}$$ Of course, \(\frac{13}{18} = 0.7222…\).
One step harder!
Let’s do one more case, which happens to tie in with the last thing we did. In looking for questions of this type, which seem to be very rare, I found this unarchived question from 2009 that takes it a step further:
I have a homework paper that I am having trouble on and I am not getting how to do it in class, but I am to scared to ask my teacher because I don't want to talk in front of the whole class.
I have to multiply an improper fraction with a decimal, but I am not sure how. I was wondering if you could explain how to get the answer.
3.2lx10 1/3
Thanks for taking your time to help me!
After dealing with a second question that I’ve omitted here, I said:
Now back to the other question, multiplying a mixed number by a decimal. I'm not sure what you were taught about this! Normally, when you have to multiply two different kinds of numerals, you rewrite one in the same form as the other, so you can multiply as usual. In your example, 3.2l x 10 1/3 we can either change the decimal to a mixed number, 3 21/100 x 10 1/3 and then multiply those by converting both to improper fractions, or change the mixed number to a decimal, 3.21 x 10.333... which is a little more awkward.
These are, of course, the same methods we’ve been discussing. Using fractions, we get $$3\frac{21}{100}\times 10\frac{1}{3} = \frac{321}{100}\times\frac{31}{3} = \frac{321\times 31}{100\times 3} = \frac{9951}{300} = \frac{3317}{100} = 33\frac{17}{100}$$
Using decimals, we have a non-terminating decimal, which gives $$3.21\times 10\frac{1}{3} \approx 3.21\times 10.333 = 33.16893\approx 33.17$$ Again, if I do the multiplication in my calculator without rounding, it shows the answer as exactly 33.17.
Not knowing if there was a specific reason the problem involved a mixed number, I suggested another method, which I probably would never do otherwise:
Were you taught something different? The only other method I can think of (and one which has some connection to your other question) is to "distribute", if you are familiar with that term. Multiplying by 10 + 1/3 is the same as multiplying by both 10 and 1/3, and adding the results: 3.21 x (10 + 1/3) = 3.21 x 10 + 3.21 x 1/3 Multiply by 10 by moving the decimal point, and multiply by 1/3 by dividing by 3. I doubt that this is what you were taught.
We find that \(3.21\times 10 = 32.1\) and \(3.21\times\frac{1}{3} = 3.21\div 3 = 1.07\), so the result is \(32.1 + 1.07 = 33.17\) yet again.
So, show me which way you think you should do it, and let me see your work. I'll guide you if you get it wrong, so don't be afraid to show me what you try. By the way, I teach adults who have trouble with some of these same things, and I'm always glad when there's someone who asks the questions the others all have! You may find that your class is waiting for someone to be bold enough to ask, and will like you more for doing so.
Katy replied,
Thank you so much! Thanks to you I aced my paper and now I understand what to do. I think it is wonderful that you take your time to help kids like me! Take care, Katy :-)
Some of our other problems above have been relatively easy, but this one was definitely worth the asking! Never be afraid to ask! But one of the reasons we’re here is to provide a private place to ask your questions and get understanding from us, in both senses of the word!

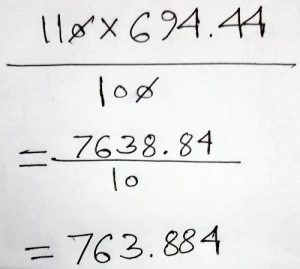
I am having trouble finding the answer to this
The Amazon rainforest covered 6.42 million square kilometers in 1994. In 2014, it covered only 50/59 as much. Which is closest to the area of the Amazon forest in 2014? (Hint: You might be able to answer the question without calculating the exact area).
Hi, Aya.
This is not really a comment, but a new question that we could handle better if you submit it to us via Ask a Question.
When you do so, please include the entire problem. They evidently listed some choices you are to pick from, and I can’t tell what they expect you to do without actually calculating, unless I see what they are. I suspect they want some sort of estimation.
But I myself would use a calculator, and just type in “6.42 × 50 ÷ 59”. Or you could do that by hand.