(An archive question of the week)
While I was researching for the post on uncountable sets, I ran across a discussion that didn’t quite fit, but raises interesting questions about how countable and uncountable sets can fit together. How can the rational numbers be countable, but the irrational numbers, which are closely intertwined with them, are uncountable?
Rationals between irrationals
Here is the question, from 2010:
Uncountable Infinitude, Illogically Concluded Regarding the question that I have seen here: Which set is bigger, the set of rational or irrational numbers? I understand both proofs: the countability of rationals and the uncountability of the irrationals. However, between each two irrational numbers we can always find a rational number. So -- to follow the same kind of reasoning that says there are the same infinite number of odd and even integers because between each two odd numbers there is an even number -- I would expect that there will be the same number (infinite of course) of rational and irrational. What is the solution to this contradiction? Where is my mistake?
To illustrate the ideas here, first think about the familiar irrational number \(\sqrt{2} = 1.4142135623730950488016887242097\dots\). We can see that this is between the rational numbers 1.4 and 1.5; or between 1.414 and 1.415; and so on. And between this and some other irrational number, there will be rational numbers like 1.414213562373. So there are irrationals between rationals, and rationals between irrationals.
Below I will be including proofs of the facts alluded to here, but it should make some sort of sense that if you choose any two irrational numbers there is at least one rational number (and in fact infinitely many of them) between, and likewise if you choose any two rational numbers there is at least one irrational number (in fact, uncountably infinitely many of them) between. Both rational and irrational numbers are “dense” among the real numbers, meaning that both types are within any interval you name. They are all packed tightly together – so much so that no picture I could make would give the idea accurately.
Boaz is picturing rational and irrational numbers sort of alternating the way even and odd numbers do:
![]()
But it is not, as he suggests, the mere presence of an even number between two odd numbers that shows that the even and odd numbers have the same cardinality; rather, we use a one-to-one correspondence that is implied by the very rigid alternation of the two (that is, that because there is exactly one odd number between any two consecutive even numbers, each odd number can be paired up with the immediately following even number). Boaz has not shown such a correspondence between rationals and irrationals! Furthermore, the real picture doesn’t look remotely like that.
I replied briefly, just noting the lack of a proper reason:
You seem to be assuming that because there is AT LEAST ONE rational between any two irrationals, and vice versa, that there are THE SAME NUMBER of each between the other. There are in fact countably (infinitely) many rationals between any two irrationals, but UNcountably many irrationals between any two rationals!
Assumptions in math can be dangerous; you need a justification for any conclusion you make! This is all the more true when dealing with infinities, which we can’t visualize. The comparison to even and odd doesn’t hold up, because those are discrete, with a definite gap between them, and only a finite number of odd numbers between any two even numbers. Infinity is much more slippery than that.
What it means to be uncountable
Boaz wasn’t satisfied, because there still seemed to be a reason for concern. He wrote back:
Many thanks for your reply. Between any two of your UNcountable irrationals, I can find a rational number. Doesn't that mean that the rationals are also UNcountable? I have seen some proofs regarding the countability of rationals, but they were not convincing. Maybe I need a more accurate proof.... (actually, I think I have two proofs, but they are probably not valid.) I hope I managed to explain my difficulty correct. Again, thanks for the prompt response!!!
This is much more convincing, on the surface: It would seem that there are uncountably many spaces between irrationals, so there must be uncountably many rationals in those spaces! Hmmm …
I replied, still pointing out that something that seems obvious from our finite experience may not be true of infinite sets, and would need proof:
You're assuming that if every member of a set A lies between two members of an uncountable set B, then set A is also uncountable. Do you have a proof of that? An uncountable set is one that CAN'T be counted. All you've done is essentially to show ONE way you could TRY to count the rationals and fail -- namely, by putting them between irrationals and realizing that you can't count those. That doesn't mean that another way does not exist. And in fact, proofs do provide a way to count the rationals. Infinities can't be trusted not to surprise you. You have to watch out for hidden assumptions such as the kind you've made.
The subtlety here lies in the negative nature of “uncountable”. To show a set is uncountable, you have to actually show that there is no way to count it, not just that one way doesn’t work, or even that no way you have found can do so.
Boaz answered the way we like to hear:
Many thanks. I think I can sleep now :-)
I know it still feels like we’ve failed to fully answer the question. We’d like a way to properly visualize what the relationship is between the rationals and the irrationals! Try this:
One way to count the rationals (within an interval, such as from 0 to 1) is to take them in order of their denominators, so we first list the halves (1/2), then the thirds (1/3, 2/3) then the quarters that are not already listed (1/4, 3/4), then the fifths (1/5, 2/5, 3/5, 4/5), then the new sixths (1/6, 5/6), and so on. As we do this, one layer at a time, each new interval we form will contain infinitely many rationals, and infinitely many irrationals. We keep descending deeper into the real number world with each increase in the denominator, picking up new rationals one by one (countably), but always leaving uncountably many irrationals still hidden between them. Here the solid dots are the rationals in the order we have counted them, top to bottom and left to right; the open dots are duplicates we don’t recount.
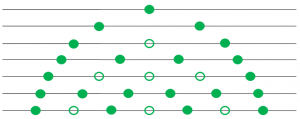
But there’s no way to put in red dots for the irrationals! At every step, there are infinitely many of both rational and irrational in every space between. All we can say is that because the rationals are countable but the reals are not, there are a lot of points in between that will not be touched, and they are “everywhere”.
Now, Boaz imagines looking at all the irrationals and putting a rational in each space between. But the uncountability of the irrationals means that we can’t carry out the process I just did with the rationals, looking at the spaces between at each step. All I can say to Boaz’s question is that it is a paradox: We can’t imagine uncountable infinity, but know that the conclusion must be true.
For more about counting the rationals, see
Set Theory and Orders of Infinity Infinite Sets Counting Rationals and Integers
Each of these uses a slightly different correspondence; the first, like mine above, deals only with numbers between 0 and 1, while the others deal with all rational numbers, positive and negative.
Proving the claims
A similar question was asked in 2000:
Do Rational and Irrational Numbers Alternate? It is known that: 1. Any two non-equal real numbers "contain" an irrational. 2. Any two non-equal real numbers "contain" a rational. These real numbers can of course be rational or irrational. Does this mean rational and irrational numbers alternate?
That is, between any two reals (including rationals) there is an irrational, and between any two reals (including irrationals) there is a rational number.
That time, Doctor Rob replied, with more formal details than I gave above, spending most of his time actually proving the two statements, and only briefly dealing with the actual question:
Yes, both statement 1 and statement 2 are true. The answer to your question, however, is "No." If that were so, the two sets would have the same size, and they don't (the irrationals are uncountable, the rationals are countable).
That was quick!
The proofs of these depend on the Archimedean Ordering Principle: if r > 0 and s > 0 are real numbers, then no matter how small r is and how large s is, there is a positive integer n such that n*r > s.
Let’s think about this, also called the Archimedean Property of the real numbers. What it says is that if I give you two numbers, say r = 0.00007 and s = 5,000,000, you can find an integer n such that 0.00007n > 5,000,000. How would you find it? Just divide 5,000,000 by 0.00007 to get 71,428,571,428.57…, and round up to 71,428,571,429. (Or anything bigger than that, like 75,000,000,000!) This says that no number is so large, and no number is so small, that you can’t exceed the former by taking steps of the latter size.
To prove the statement 2, for example [there is a rational between any two reals], let the two unequal real numbers be x < y. Then let r = y - x > 0, and s = 1 + r. Then by the A.O.P., there is a positive n such that
n*r > 1 + r,
n*y - n*x > 1 + r,
n*x < n*y - r - 1.
Now consider integer m = [n*y-r]. (Here [x] means the greatest integer less than or equal to x, that is, the integer you get by rounding down from x. It satisfies x-1 < [x] <= x.) Then we can see that
n*x < n*y - r - 1 < m <= n*y - r < n*y,
x < m/n < y.
Thus m/n is a rational number in the interval (x,y).
To get an irrational number in the interval (x,y) [statement 1], let z be any positive irrational number. Now use the above argument to find a rational number m/n in the interval (x/z,y/z). Then z*m/n will be in (x,y) and irrational.
To see what’s going on here, let’s find a rational number between the real numbers \(x=\sqrt{50}\) and \(y=\sqrt{51}\). (That can be done more easily using specific properties of radicals; I’ll do it here using Doctor Rob’s generally applicable method.)
I’ll use the more modern notation \(\left \lfloor x \right \rfloor\) for the “floor”, or “greatest integer”, function, for clarity; this wasn’t available on the old site.
Let \(r=\sqrt{51}-\sqrt{50}\approx0.07036\). The Archimedean Property implies that there is some integer n by which we can multiply this to get a product greater than \(s = 1 + r\) (which for our example is 1.07036); we can find it by dividing and rounding up:\(16\cdot0.07036\approx1.12577>1.07036\)). Now we let \(m=\left \lfloor ny-r\right \rfloor=\left \lfloor 16\cdot\sqrt{51}-0.07036\right \rfloor=114\). Our fraction is therefore \(\frac{m}{n} = \frac{114}{16} = 7.125\). This is in fact between \(\sqrt{50} \approx 7.07107\) and \(\sqrt{51} \approx 7.14143\).
Next, let’s find an irrational number between, say, \(x = \frac{7}{52}\approx0.134615\) and \(y = \frac{7}{51}\approx0.137255\). Let \(z = \sqrt{2}\), arbitrarily. We want to find a rational number between \(\displaystyle\frac{x}{z} = \frac{\frac{7}{52}}{\sqrt{2}}\approx 0.095187\) and \(\displaystyle\frac{y}{z} = \frac{\frac{7}{51}}{\sqrt{2}}\approx 0.097054\).
Doing the same things we did in the last paragraph, we let \(r=0.097054-0.095187 \approx 0.001866\). Our n will be 1.001866/0.001866, rounded up to 537.
Now we let \(m=\left \lfloor ny-r\right \rfloor=\left \lfloor 537\cdot0.097054-0.001866\right \rfloor=52\). So our m/n is 52/537; and our irrational number is \(\displaystyle z\left(\frac{m}{n}\right) = \sqrt{2}\left(\frac{52}{537}\right) \approx 0.136944\). And this is an irrational number in the right interval.
(Note that there is no actual value in these calculations themselves, because the numbers we found are just approximations to the irrational numbers we’re really talking about. What matters is that the exact values are demonstrably just what we say they are.)

This is the only article I have found (in my short search) that answers exactly this question. Absolutely brilliant article clearly explained. Most sources regurgitate the proofs. I understand the proofs but not always the implications. This teases out the subtle distinctions in a wonderful way. Thank you so much!
Thanks. A big part of the fun of a site like ours has been that questions like this force us to think through ideas in ways one doesn’t when just preparing an article from scratch!