(A new question of the week)
Sometimes a topic you think you know looks entirely different in an unfamiliar context. Here, a returning student faces a quadratic equation where x and y are reversed, making the quadratic formula seem foreign! But this is when real learning happens, when you are forced to think through the meaning of what was previously just a rote process.
What is the quadratic formula for?
The question came to us in late August, from Mike, a recent repeat user of the site:
Hello Again,
I am back with some more basic precalculus stuff. Hope you all are well. Anyway, in the equation set I’m currently working on I’ve come across something I haven’t seen before. The question is:
y^2 – 4y – 8 = 3x
Find the x and y-intercepts.
I was able to find the x-intercept no prob. Finding the y-intercept not so much. As far as I understand, the quadratic formula is only applicable to determining the x coordinate of a function? Any clarification on that topic would be helpful. Tried combining like terms and still was unable to figure it out. Any help would be greatly appreciated.
Thanks Math Doctors.
Such a question is usually asked of an equation representing a function of x. Here, both variables play the same role, as we have an “implicit” equation. Is there a function here? How do we find the intercepts?
Mike knows that the x-intercept is the value of x where the graph crosses the x-axis; that is, where y = 0. If we replace y with 0, we get:
$$y^2 – 4y – 8 = 3x$$
$$(0)^2 – 4(0) – 8 = 3x$$
$$-8 = 3x$$
$$x = -\frac{8}{3}$$
But to find the y-intercept, he has to solve
$$y^2 – 4y – 8 = 0$$
and that seems unfamiliar. The equation can’t be solved by factoring; but the quadratic formula is always written with an x: $$ax^2+bx+c=0$$ $$x = \frac{-b\pm\sqrt{b^2 – 4ac}}{2a}$$
Doctor Fenton answered:
Hi Mike,
Since you haven’t shown any of your actual work, you have only given a verbal description of what you have done and want to do, I can’t tell exactly where you are having difficulty.
You may be misinterpreting the Quadratic Formula, since your description of it says “the quadratic formula is only applicable to determining the x coordinate of a function”.
The quadratic formula is a method for finding the roots or zeros of a quadratic equation. That equation is usually written in terms of an unknown variable x,
ax2 + bx + c = 0 ,
but the letter x is irrelevant: the important feature is the pattern of the equation. The variable can represent anything, and can be designated using any letter or symbol: the equations
ay2 + by + c = 0 , at2 + bt + c = 0 , and au2 + bu + c = 0
all represent the same pattern, and the quadratic formula applies to each one in the same way.
A quadratic always has the same form: a constant (here represented by the letter a) times the square of the variable, plus another constant (b) times the variable, plus a third constant (c), and the right side of the equation is 0. The values of the variable which satisfy this equation are
-b ± √(b2 - 4ac) x = ----------------- 2a(and this equation is really two different equations, one with a + sign in the numerator, and a second equation with a – sign in the numerator).
By teaching the formula always using x as the variable, we make it easier to memorize, but also easy to associate too tightly with that particular variable! Doctor Fenton’s emphasis on the pattern of the equation is a useful perspective. The variable x (and, indeed, also the parameters a, b, and c) are “placeholders”, which are meant to be replaced by whatever numbers and/or variables play those roles; it is not their names, but their roles and relationships that matter.
He continued:
If the variable is denoted by y instead of x, we can then say that the values of y for which the equation is true are
-b ± √(b2 - 4ac) y = ----------------- . 2aDoes this help? Can you find the y-intercepts from this information?
If you still have difficulties or questions, please write back and show me what you have been able to do, and what difficulties you are having, and I will try to offer further suggestions.
Functions and equations
Mike responded with three questions, which I will interleave with Doctor Fenton’s answers. First:
Thank you for the response, and yes your information is very helpful. It’s funny, the way that my textbook explains the quadratic formula is poor at best, so understanding that it is specifically designed for determining the roots (zeros) of a function is of great conceptual value to me. Thank you for that. Quick question, what is the actual difference between a function and an equation?
In his question, Mike had focused on the formula finding x; changing that to “roots” (solutions of an equation) or “zeros” (values that make a function equal to zero) put the focus in the right place.
Doctor Fenton responded:
To answer your first question, you can think of a function as a rule which assigns a unique value to each input. For example, if you throw a ball vertically upward from a height of 10 feet at 30 feet per second, then the height of the ball t seconds later is h(t) = 30t – 16t2+10 (if we take the acceleration due to gravity at 32 feet per second per second). For each positive value of t (assuming the ball was released at t=0), this formula gives the height of the ball at that time, so we say that height is a function of time.
An equation is a statement of equality between two expressions. The expressions often contain an unknown quantity which we wish to determine, which is called “solving the equation”. Your question involves a function y2 – 4y – 8 = x, in which x i s a function of y. When you set x=0 to find the y-intercepts, you get the equation
y2 – 4y – 8 = 0
which you want to solve for the values of y which are associated with x = 0.
(The original equation actually was $$y^2 – 4y – 8 = 3x$$ which would have to be divided by 3 to express x as a function of y, but that doesn’t affect the y-intercepts.)
Finding the y-intercepts amounts to finding the roots of the equation \(y^2 – 4y – 8 = 0\), or equivalently finding the zeros of the function \(f(y) = y^2 – 4y – 8\).
Solving the original problem
Mike continued with his second question, just asking for a check on his work:
In regard to the question I had asked, when checking my answers in the answer key, it seems that the book just arbitrarily rounded up the y-intercepts I originally found to whole numbers (although the actual question asked for answers rounded to two decimal places.) That being said, I believe I found the correct answer the first time around, it being:
y2 – 4y – 8 = 3x
y-int:
y2 – 4y – 8 = 0
(can’t factor, so QF):
y = [4 ± √ (-4)2 – 4(1)(-8)] / [2(1)]
y = [4 ± √ 48] / 2
y = 2 ± 2√3
y-int = (0,-1.46) , (0,5.46)
Checked using graphing utility, and seemed to be right but just wanted to clarify with the Doctors.
(He had a further question, which I’ll show after we look at the response to this part. In the above, I have added brackets, [ ], that he omitted, which are necessary in order for it to mean what he intended. This is common, and we usually can figure out what was intended, but sometimes we have to ask.)
Here is the graph, showing all three intercepts and the vertex:
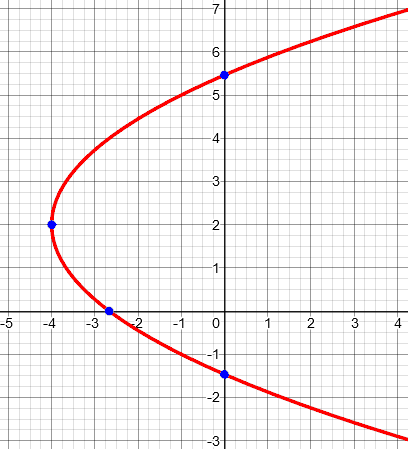
There was not much for Doctor Fenton to say:
Your solutions for the y-intercepts using the Quadratic Formula are correct.
Evidently the back-of-the-book answers were -1 and 5, rounded more than they were supposed to be, and Mike really had the right answers from the start.
Cube roots are different
Mike’s third question changed things (again I’ve inserted brackets to correct some equations):
I had also worked on another problem from the same problem set which also asks for the x-intercepts, the problem is:
2xy – x3 – 5 = 0
(I got what I assume is the right answer but wanted to clarify the justification of my mathematical reasoning with you as well, as it is conceptually not as clear to me)
After redistributing the equation I got: y = [5 + x3]/ [2x]
x-int: 0 = [x3 + 5] / [2x]
0(2x) = x3 + 5
0 = x3 + 5
x3 = -5
x = ³√-5
x = -1.71 and/or 1.71
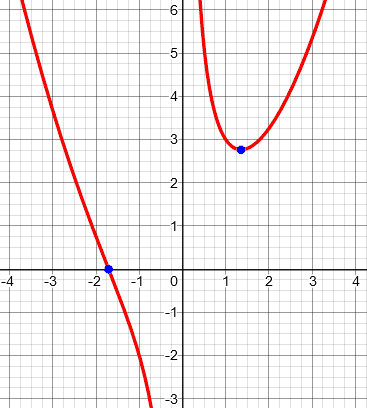
After plugging in both x-intercepts I found that x = 1.7 did not satisfy the equation. Therefore the only root (of both the x and y-intercepts) is (-1.7, 0 ).
It seems to be correct on paper but something about the way in which is was deduced has left me unsure, maybe it’s the cube root, just seems incorrect somehow (as in having a negative under the square root).
The issue is, why didn’t both solutions work? Here is a graph to confirm the conclusion:
To this, Doctor Fenton replied:
In your second problem, you correctly solved the equation for y, and set y = 0 to find the all the x-intercepts. You are correct that a fraction such as
x3 + 5 -------- = 0 2xonly if the numerator is 0 and the denominator is non-zero. That means that
0 = x3 + 5, so x3 = -5.
However, while your solution
x = ³√-5
is correct, your following conclusion
x = -1.71 and/or 1.71
is not.
When a non-zero number is squared, the result is always positive, and that means that every positive number has two square roots. Since 52=25 and (-5)2 = 25, both 5 and -5 are square roots of 25. Since we often want only the positive root, it is a convention that whenever we write √a for any positive number a, this symbol means only the positive square root. If we want to consider both square roots, we write ±√a .
But cube roots are different. Every real number has exactly one cube root, so when you take a cube root to solve x3 = -5, you do not write x = ± ³√-5. There is only one cube root of -5, ³√-5 = -1.70997595. The cube root of a positive number is positive, and the cube root of a negative number is negative.
So there is only one x-intercept in this case.
Thanks
Mike had one more thing to say:
I just wanted to say thanks for the responses (always so quickly, even on weekends; you guys are great). Incredibly helpful and cleared everything right up. I feel foolish about the cube root thing, can’t believe I forgot about that simple relationship pertaining to negative numbers to the power of three.
I have been in contact with you and your colleagues for a bit now off and on, and I have to say this is even more helpful than my any of my TA’s were at university. I had to leave university in my early 20’s (due to personal afflictions which have since improved greatly) and am going to be returning to the academic arena next year, hence why I am getting reacquainted with mathematics (stopped pursuing math while in first year calculus). It’s amazing how much you forget in such a relatively short time. I just wanted to thank you and your colleagues, as you have helped me greatly when I have been recently stumped or just plain forgetful. I plan on coming to your team for aid even upon my return to school. Thanks for everything, sincerely.
This is why we exist.
