Infinitely Truncating a Triangle

(A new question of the week)

Here is an intriguing question we got at the end of September from an adult whose name I’ll shorten to Arun.

Dear Sir

Let P_o be an equilateral triangle of area 10. Each side of P_o is trisected, and the corners are snipped off, creating a new polygon (in fact, a hexagon) P₁. What is the area of P_i? Now repeat the process to P_i – i.e. trisect each side and snip off the corners – to obtain a new polygon P₂. What is the area of P₂? Now repeat this process infinitely often to create an object P_∞. What is the area of P_o?

Here is my working for the above problem:

I have two questions regarding this problem.

1. I have calculated an approximate value to the answer by using brute force method. Is there a closed form for the given series?
2. I thought that since three sides of the subsequently generated polygon always lie on the parent triangle and this shrink to a point in the infinite limit, the resulting limiting figure should be the incircle.

But area of corresponding incircle is 10π/(3√3) = 6.046.

So is there a mistake in the geometric interpretation or calculation?

Thanks in advance.

There is some very good work here. Because Arun did not define the variables, it’s hard to say how close it is to being correct; but there is much in the work that we will see below. I suspect there is a wrong assumption about the shape of each triangle removed.

Here is the construction with three levels of truncation (the first truncation in red, the second in orange, the third in yellow, the remaining figure shown in green):

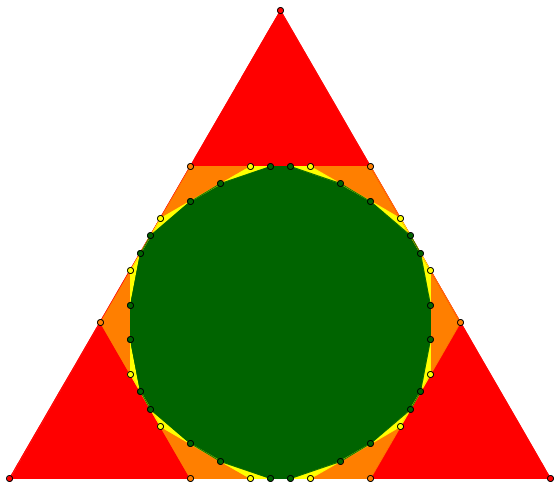
I constructed this using GeoGebra (using a trisection tool to speed the work); the areas of the successive polygons are reported as 10, 6.6666, 5.9359, and 5.7613. If we repeat the truncations, we can see that the area will only decrease, so Arun’s estimate of 5.82 is too large. We can also see that his guess that the result would be the incircle (inscribed circle) of the triangle is wrong:

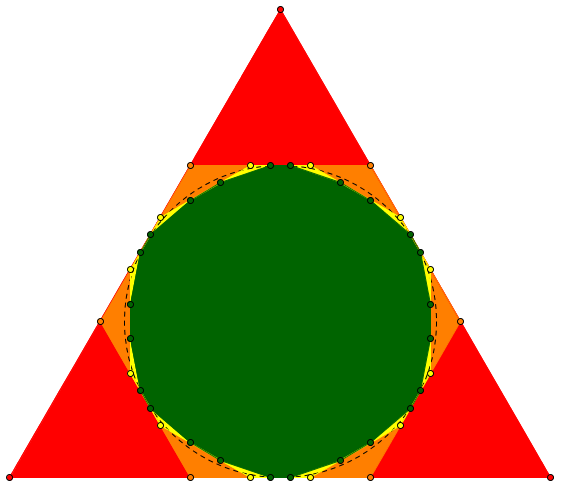
The incircle, shown as a broken line, has area 6.046, just as Arun calculated. (The incircle of an equilateral triangle has radius \(\displaystyle\frac{s\sqrt{3}}{6}\), so its area is \(\displaystyle\frac{\pi s^2}{12}\). The area of the triangle itself is \(\displaystyle\frac{s^2\sqrt{3}}{4}\), so the ratio of incircle to triangle is \(\displaystyle\frac{\pi\sqrt{3}}{9} = 0.6046\).)

Doctor Rick answered:

The more I looked at this problem, the harder it seemed — until I noticed something simple.

What made it look even harder than your work shows, is that after the third iteration (that is, the third set of triangles removed), the triangles to be removed next are no longer all congruent to one another. Thus, it seems as though the next step beyond what you did will have added complexity.

What I realized eventually was that I didn’t have to work with angles, or with the shapes of the triangles in any way, only with ratios of areas. To start with, each of the three triangles removed in the first iteration has area 1/9 of the equilateral triangle from which they are removed, thus the total area removed at this step is 3 × 1/9 × 10. What about the second iteration — how does the area of each triangle removed compare to the areas of those removed in the previous iteration?

Regarding your conjecture that the final area should be that of the incircle, I don’t have a lot of confidence in that argument. The polygons are not all circumscribed about the incircle; I do not believe the polygons will approach the incircle in the limit. Therefore if I get a result that differs from that conjecture, I would reject the conjecture rather than my work. What the limiting shape actually is, however, I do not know!

We’ve seen above that the limiting figure definitely is not the incircle.

Here is a closeup of the lower left corner of my figure:

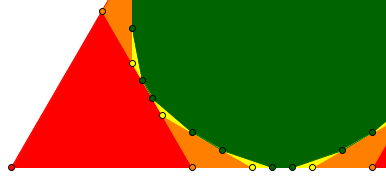
The second triangle (orange) has both height and base equal to \(\frac{1}{3}\) of the first triangle (red), so its area is \(\frac{1}{9}\) of the first. Does that continue to be true forever, even though the removed triangles from here on will not all be congruent?

Arun replied:

I’ll try again along the lines suggested by you and get back to you.

Thanks.

After waiting a long time for further progress, Doctor Rick wrote back, because the problem was too interesting to drop:

It’s been nearly two weeks. Have you done any more thinking about this problem?

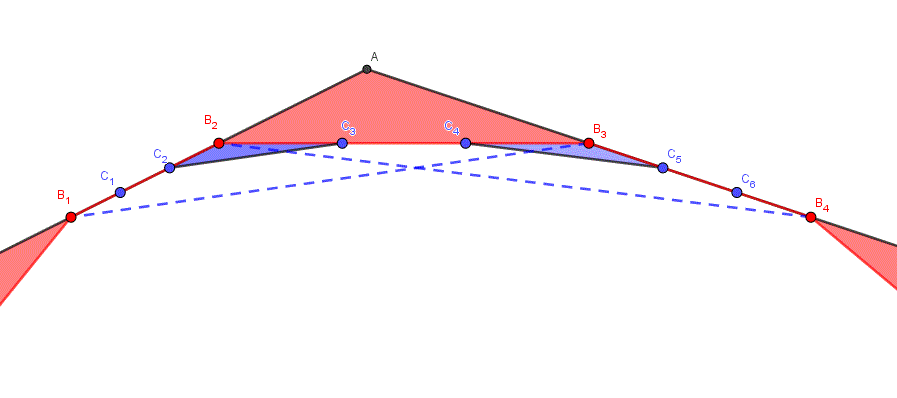
I want to share a figure that might clarify the idea I hinted at. In this figure, vertex A and the black line segments are part of the polygon at some iteration k–1 of the process. Vertices B_i and the red lines are part of the polygon at the next iteration, k; vertices C_i and the blue lines are part of iteration k+1. The red triangle AB₂B₃ is one of those removed in iteration k; the blue triangles B₂C₂C₃ and B₃C₄C₅ are among those removed in iteration k+1.

Using the figure, can you see how the area of the blue triangles is related to the area of the red triangle? The dashed blue lines might help you; they helped me to get this idea initially

We can see that triangle B₁B₂B₃ has the same area as AB₂B₃, and C₂B₂C₃ is similar to it, with \(\frac{1}{9}\) of the area as we saw above. And since this drawing represents any corner of the figure, at any stage, we know that all this is true despite other triangles not being congruent.

After another week, Arun was free to respond:

Sorry for not replying earlier, but I got into a fix. I’ve shown my working in the attached file. Kindly go through it and let me know whether I have grasped your hint properly.

Sorry. Wherever I said 1/3, I meant 1/9. So, an infinite geometric progression of common ratio 2/9.

This amounts to the same reasoning I gave above, with different letters (once we replace the \(\frac{1}{3}\) with \(\frac{1}{9}\)). The calculations at the end are an attempt to check that the two triangles do have the same area, using the method of the original work. Since it is obvious that triangles ABC and BFC have the same area (equal base and same height to C), the area calculations must be wrong.

Doctor Rick replied:

Thanks for getting back on this!

You erred in your calculation of the area of triangle BFC because, apparently, you used a as the length of both sides BF and BC. In fact, the length of BC is a√3.

Now you should see that the 2/9 common ratio for the series is consistent with the calculated ratio of areas for this first step, and you’re on the right track.

So the only error was in the check; the actual work toward the solution was all good.

And that was it:

Thanks Dr. Rick,

I’ve understood my error and got the solution. Thanks again for being patient with me.

Kind regards

To which Doctor Rick replied,

You’re welcome. I enjoyed the problem and I’m glad we could bring it to a good conclusion.

But let’s finish up ourselves. We are starting with an area of 10, and subtracting \(\frac{1}{3}\) of that, then \(\frac{2}{9}\) of that, and so on: $$\text{Removed area}=10\left[\left(\frac{1}{3}\right)+\left(\frac{1}{3}\right)\left(\frac{2}{9}\right)+\left(\frac{1}{3}\right)\left(\frac{2}{9}\right)^2\dots\right] = \frac{10}{3}\left(\left(\frac{1}{1-\frac{2}{9}}\right)\right)=\frac{10}{3}\cdot\frac{9}{7}=10\frac{3}{7}$$ so the remaining area is \(10\cdot\frac{4}{7}=5\frac{5}{7}\approx 5.714\), which agrees with the sequence of areas I measured at the top.