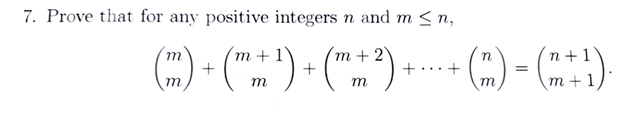We’ll first look at several old questions about proving a relationship between permutations or combinations, where we’ll see some algebraic proofs using formulas, and others that center on the meaning of the symbols as ways of counting. The latter are called “combinatorial proofs”. We’ll end with a recent question of the same type, which suggested this post..
C(n, r) C(r, k) = C(n, k) C(n-k, r-k)
We’ll start with a question from Scott in 1996:
Combinatorial Proof I'm trying to do a combinatorial proof on C(n,r)C(r,k) = C(n,k)C(n-k,r-k) where k <= r <= n. I have the hint "think of choosing a subset of k elements and another, disjoint, subset with r-k elements." Unfortunately, I can't really find a "formula" for this type of proof so other than the hint I'm not sure where to go with it. My book just has one example and it is for Pascal's identity. Can you maybe give me a better hint?
Pascal’s Identity is the fact, using this notation, that C(n, r) + C(n, r+1) = C(n+1, r+1). We explored how to prove this, both algebraically and combinatorially, in Writing a Proof: Substance, then Style. Using two other notations, it can be written as $$_n\mathrm{C}_k\,+_n\!\mathrm{C}_{k+1}=\,_{n+1}\mathrm{C}_{k+1}$$ or $${n\choose k}+{n\choose {k+1}}={{n+1}\choose{k+1}}$$ The fact we are to prove here is $${n\choose r}{r\choose k}={n\choose k}{{n-k}\choose{r-k}}$$
Recall the definition of combinations (see Permutations and Combinations: An Introduction): $${n\choose r}=\,_n\mathrm{C}_r=\frac{n!}{r! (n-r)!}=\frac{\underset{r\ factors}{\underbrace{n(n-1)\cdots (n-r+1)}}}{\underset{r\ factors}{\underbrace{r(r-1)\cdots (1)}}}.$$
An algebraic proof
Doctor Anthony answered first, giving an algebraic proof:
This can be proved very quickly if you use the formula for nCr.
nCr = n!/(r!.(n-r)!) Apply this to equation you quote.
nCr*rCk = nCk*(n-k)C(r-k)
n! r! n! (n-k)!
-------- * -------- = -------- * ------------
r!(n-r)! k!(r-k)! k!(n-k)! (r-k)!(n-r)!
If you cancel r! on top and bottom lines of the left hand side, and (n-k)! on top and bottom lines of the right hand side then each side reduces to
n!
-------------- and so the two expressions are equal.
(n-r)!k!(r-k)!
Scott replied:
I understand what you wrote, but that isn't a "combinatorial proof", is it? Isn't it just a proof based on the def of nCr?
Yes. A combinatorial proof is one in which we interpret combinations in terms of actually choosing r things out of n, and show that the same quantity can be counted using either of two expressions, which are therefore always equal.
A combinatorial proof
Now Doctor Sydney answered:
Dear Scott, I'm glad you wrote back. Dr. Anthony gave a nice algebraic proof of the equality, but you are right that it wasn't a combinatorial proof. Combinatorial proofs rely on counting arguments, not algebraic manipulation. So, let's see if we can work out a combinatorial proof to this problem.
Algebra is often routine and straightforward, applicable to any problem once it is put into algebraic terms; a combinatorial proof requires more ingenuity (and thus is more fun!) and sometimes more convincing.
When I am working on combinatorial proofs, I find it easier to have just one thing on one of the sides of the equation, because that way it is easier to put into words what a given quantity represents. Thus, rather then trying to prove the equation in the form it is above, I would rewrite the equation as follows: Prove that : C(n,k) = C(n,r)C(r,k)/C(n-k,r-k) That way, I can clearly understand what at least one of the sides of the equation is trying to represent. Here, in this case, I know that the left hand side of the equation represents the number of ways to choose k objects from n objects. Then, the only thing left to do is show that the right hand side of the equation also represents the number of ways to choose k objects from n objects.
We’ll see a direct approach, without the rewrite, after finishing this method.
So, let's attempt to do just that. First, let's think about what the numerator represents. C(n,r) is the number of ways to pick up r objects from a set of n objects, and C(r,k) is the number of ways to pick up k objects from a set of r objects. So, what would multiplying these values together represent? It would be the number of ways of choosing k objects from n objects in the following manner: We first choose a set of r objects from the set of k objects, and then from those r objects, we choose a set of k objects. So, basically, it is the number of ways to choose k objects from n objects, except that it overcounts. It is hard to put into words -- this is something you kind of have to think through on your own.
We’ve seen overcounting before, in Permutations and Combinations: Undercounts and Overcounts. Here, the idea is that we can get the same set of k objects as part of any set of r objects that contain them, so we’ve counted the same set more than once.
I often find it helpful to experiment with a small example in order to understand it better. Here, suppose that \(n=3\), \(r=2\), and \(k=1\). How many ways are there to choose 1 of 3 objects? \(\displaystyle{n\choose k}={3\choose 1}=3\):

If we choose 2 balls first, and then choose 1 of those, we have \(\displaystyle{n\choose r}={3\choose 2}=3\) ways to choose the pair:

Then for each of those pairs, there are \(\displaystyle{r\choose k}={2\choose 1}=2\) ways to choose one from it:
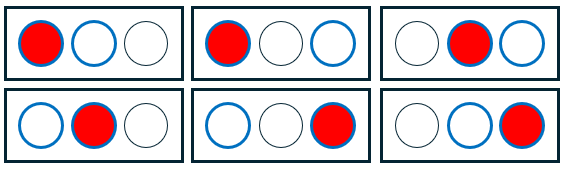
So there are \(\displaystyle{n\choose r}{r\choose k}={3\choose 2}\cdot{2\choose 1}=3\cdot2=6\) ways to take the two steps.
Clearly we have to divide this by 2 to get the correct number. We just need to see where this comes from.
To finish up the proof, we must figure out how to account for this "overcounting." Okay, so to be honest, if we believe that the equation is true, we only have to explain why dividing by C(n-k,r-k) takes care of the overcounting. But let's try to figure out by how much we overcounted when we did the C(n,r)C(r,k) counting thing. In other words, given a set of k items, how many times did we count it? Well, every time that set of k items was in the set of r that we chose in the first step, we counted it, right? So how many times is a given set of k items in a set of r items?
In our example, we have to divide by 2. What formula gives this?
Let's figure this out. We have n items total, and we want to know how many sets of r items contain a given set of k items. Well, if we have a set of r items containing our given set of k items, then we know for sure that those k items are in the set of r items (duh!). So, how many choices do we have for the other r-k items? Well, we can choose the other r-k items from the remaining n-k items (remember that we've already designated k items to belong to our set), so we have C(n-k,r-k) ways to do this. Thus, each set of k items belongs to C(n-k,r-k) sets of r items, and thus each set of k items was counted C(n-k,r-k) times.
So our \(\displaystyle{{n-k}\choose{r-k}}={{3-1}\choose{2-1}}={{2}\choose{1}}=2\) represents the number of ways to choose an extra object from the 3 to fill up a set of 2.
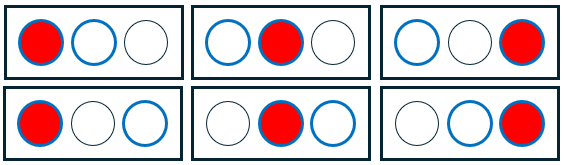
In effect, we’re working backward from the r chosen objects to the possible sets of k they can be chosen from.
From here on out, I'm sure you can fill in the details for the proof. I hope that helps and makes sense. If this way doesn't make sense, you can try to approach it by proving the equation as it is written and translating each side into understandable language and showing that they are equal. Essentially, combinatorial proofs boil down to providing two different ways to count something. They are nice, because they are fairly flexible -- you can go about them in several different ways.
A simpler version
Five years later, reader Rob Pratt wrote with a direct approach, which is just the method I like:
On 7/16/96, Scott Turner asked for a combinatorial proof of C(n,r) C(r,k) = C(n,k) C(n-k,r-k). The identity becomes clear when one thinks of committees and subcommittees. Both sides count the number of ways to select, from among n people, a committee of r containing a subcommittee of k. For the left-hand side, we first select the r committee members and then select the k subcommittee members from among these r. For the right-hand side, we first select the k subcommittee members and then select the remaining r-k committee members from among the remaining n-k people.
So the LHS, \(\displaystyle{n\choose r}\cdot{r\choose k}\), represents the ways to choose, in our example, a committee of 2 and a “subcommittee” of 1 within it,

while the RHS, \(\displaystyle{{n}\choose{k}}\cdot{{n-k}\choose{r-k}}\), represents the ways to choose a “subcommittee” of 1, and then 1 more to join it in the committee of 2:

These are the same set of 6 possibilities. We’ll see a similar style of thinking later.
Can you see how this fits the hint, “think of choosing a subset of k elements and another, disjoint, subset with r – k elements”? We are choosing the subcommittee of k people, and then an additional \(r-k\) to fill out the committee of r.
C(n, 0) = 1
Here is a quick question from 2003:
C(n,0) = 1 How is C(n,0)=1, where n is an integer?
The fact that $${n\choose 0}=1$$ for any n might be confusing either for algebraic reasons, or in terms of the meaning of combinations.
Doctor Samus answered, from both perspectives:
Hi Saurav,
To see why C(n,0) = 1, for n an integer, we must look at the formula for C(n,r), when n is an integer, and r is an integer 0 <= r <= n. It is:
n!
C(n,r) = -------- (where a! = (a)*(a-1)*(a-2)*...*2*1)
r!(n-r)!
So if r = 0, then we have:
n!
C(n,0) = --------
0!(n-0)!
n!
= -------- (since we define 0! = 1)
n!
= 1
This assumes you know and understand that \(0!=1\). That is discussed in Zero Factorial: Why Does 0! = 1 ?, which includes discussion of the meaning of permutations and combinations along the lines of the combinatorial explanation that follows.
Another way to think of it is that C(n,r) can be interpreted as the number of ways you can select r elements from a set of n elements. How many ways can we take 0 elements? Only one: by taking none.
This may feel odd at first, but it grows on you.
Another simple, and very useful fact, is that $${n\choose k}={n\choose {n-k}}$$ for any n and k.
This, combinatorially, is because choosing k out of n objects to include means the same as choosing \(n-k\) of the n to exclude. Here, again, we have counted the same thing in two ways, showing that the two formulas are equal.
C(2n, 4) = 2C(n, 4) + 2C(n, 3) C(n, 1) + (C(n, 2))^2
Now let’s look at a bigger one, also from 2003:
Combinatorial Proof: Identity I don't understand how combinatorial proof is meant to work. I have read textbooks and it still makes no sense to me. Here is an example: C(2n,4) = 2C(n,4) + 2C(n,3)C(n,1) + (C(n,2))^2 for all n in N; n >= 4
We want to prove $${{2n}\choose 4}=2{n\choose 4}+2{n\choose 3}+{n\choose 2}^2\;\;\text{ for }n\in\mathbb{N},n\ge4$$
To use combinatorial reasoning, we first observe that the goal (LHS) is to choose 4 out of an even number of objects, and the RHS involves choosing 4 or less from half as many at a time. This suggests we think of the total set as two groups of n, and select some from each group.
Doctor Anthony answered concisely:
We are using a combinatorial argument to prove the identity above. The argument is clearer if we let n have a particular value, but the reasoning is perfectly general. Suppose n = 5, so 2n = 10 and we require to find the number of ways that 4 things can be chosen from 10 different things. For convenience let the 10 things be the letters a,b,c,....i,j.
Again, picturing the situation with specific small numbers is useful for understanding what to do, and checking that it makes sense. This time we won’t be trying to show all possibilities, just to visualize examples. Here we have two sets of 5, and want to pick any 4 from all 10, which we can do in \(\displaystyle{{2n}\choose 4}={{10}\choose 4}=210\) ways; here is one of them:
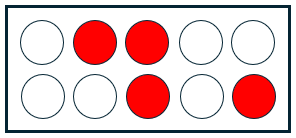
Then we divide the 10 things into two groups of 5, that is, letters a,b,c,d,e and f,g,h,i,j
a,b,c,d,e | f,g,h,i,j Number of selections
----------|-------------------------------------
b,c,d,e | = C(5,4)
|
| f,h,i,j = C(5,4)
|
b,c,e | h = C(5,3) x C(5,1)
|
c | f,h,j = C(5,1) x C(5,3)
|
a,d | h,j = C(5,2) x C(5,2)
These are all the ways we can take the four chosen objects from the two rows, described in terms of examples (for example, “b, c, d, e” is one particular way to choose 4 of the top row, “a, b, c, d, e”). The first two examples take 4 from one row; the next two take 3 from one row and 1 from the other; the last takes 2 from each row.
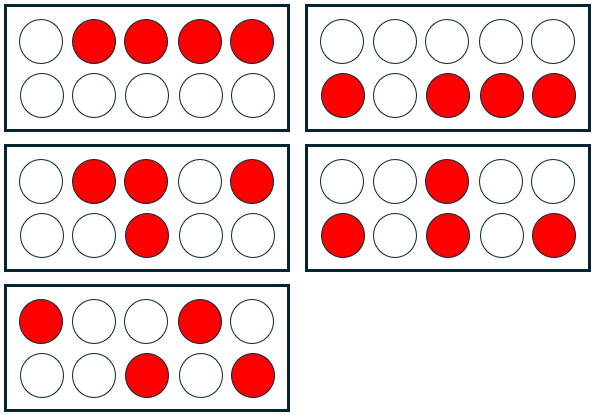
This covers all possible ways of selecting 4 things from 10 different things. So C(10,4) = 2.C(5,4) + 2.C(5,3).C(5,1) + [C(5,2)]^2 and the identity is proved.
Indeed, $$2{{5}\choose 4}+2{{5}\choose 3}{{5}\choose 1}+{{5}\choose 2}^2=2(5)+2(10)(5)+(10)^2=210$$
To make an actual proof, we’d just use a variable in place of the specific number 5.
C(m, n) + C(m+1, n) + … + C(n, m) = C(n+1, m+1)
We’ll close with the recent question, from Joash in early April:
I am struggling to answer this question in a logical way.
I can see that the LHS of the equation essentially counts all possible committees of m members out of a list of options of size between m and n (inclusive). So essentially if m = 5 and n = 10 then it would count all possible committees of 5 individuals out of anywhere between 5 and 10 possible committee members.
However I’m struggling to break down the RHS of the equation so it matches the LHS. Logically I just can’t see how picking a committee of m+1 members from n+1 possible options is the same as the LHS.
Joash is starting with the same ideas we’ve seen above: considering the meaning of each side, imagining an example with relatively small numbers, starting with the RHS, which is a single expression. All I could suggest was to use a smaller example, more literally.
I answered:
Hi, Joash.
I’ll tell you how I started.
I took a small example, with m=3, n=5. I checked that it is true that 3C3 + 4C3 + 5C3 = 6C4, in case the claim might be false. (1+4+10=15)
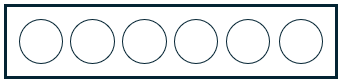
Then I drew 6 dots, and thought about how I might count ways to choose 4 of them to color in, that might involve choosing 3 out of 3, 4, and 5.
Here I’ll use 6 letters instead: ABCDEF. I want to choose 4 of them.
In particular, I decided to start from the right end of the LHS, using 5C3 first. That made sense: If I choose A, then I still have to choose 3 of the remaining 5.
What if I don’t choose A? Keep going.
Once you see this in the small case, then you can generalize to any m and n.
(When I was finished, I noticed that the thinking is similar to an induction proof; or you might think of it as a recursive process: Just keep doing the same kind of thing.)
Let’s use dots.
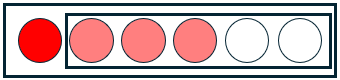
If I choose the first dot, I need 3 more:
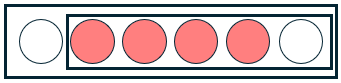
If I don’t choose the first, I need to choose 4 of the remaining 5:
Joash replied with a partial answer:
I have done what you said and drew the arrangement as 6 letters and I think I understand now. Just to check with you, would it be accurate to say…
The RHS takes n+1 options in a line and goes from the left, selecting the (m+1)th option as a “point of no return” essentially. Then it goes from the right and counts all possible committees until it reaches the (m+1) point of no return at which point going further would mean trying to pick a committee of size m where the remaining options are < m. Therefore the RHS essentially counts the same thing as the LHS, meaning they are equal.
I may be wording this incorrectly but I think I do understand it
I responded:
I’m not sure I follow your details, but you’re probably at least in the right ballpark. Mostly, I’m just not sure what you mean by “point of no return”.
Here’s my thinking, in terms of my small number example, which can be easily generalized:
We have m=3, n=5, and want to see that 3C3 + 4C3 + 5C3 = 6C4. That is, we want to see that we can choose 4 of 6 objects in 3C3 + 4C3 + 5C3 ways,
So we want to partition the process into three cases.
So here are 6 objects, of which I want to choose 4:
ABCDEF
I first decide whether to take A.
If I take A, then I have to choose 3 of the remaining 5; I can do that in 5C3 ways.
If I don’t choose A, I have to choose 4 of the remaining 5,
BCDEF
Now I can repeat the same process:
If I take B, then I have to choose 3 of the remaining 4; I can do that in 4C3 ways.
If I don’t choose B, then I will have to choose 4 of the remaining 4,
CDEF
But 4C4 is 1, which is the same as 3C3! (Or, I could say that I have to choose C, and then have to choose 3 of the remaining 3, in 3C3 ways.)
So the total number of ways to choose 4 of 6 is 5C3 + 4C3 + 3C3.
This can be generalized, and explained more directly.
Here is a visual version: We can choose 4 of 6

in one of these three ways:
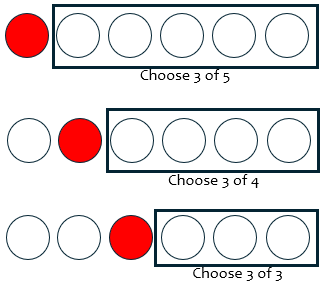
So the kth term in our sum is the number of ways to choose \(m\) more objects when the first object we take is the kth object of the \(n+1\).
Now let’s try to turn this example into a proof.
We want to count the ways to choose \(m+1\) out of \(n+1\) items. We can split these into two groups: Either we take the first object, and then need to take m of the remaining n object; or we do not take the first object, and need to take \(m+1\) out of the remaining n objects. So $${{n+1}\choose{m+1}}={{n}\choose{m}}+{{n}\choose{m+1}}$$
But by the same reasoning, replacing \(n+1\) with n, $${{n}\choose{m+1}}={{n-1}\choose{m}}+{{n-1}\choose{m+1}}$$
Combining these, $${{n+1}\choose{m+1}}={{n}\choose{m}}+{{n-1}\choose{m}}+{{n-1}\choose{m+1}}$$
We can repeat until the last term is \(\displaystyle{{m+1}\choose{m+1}}=1\), and replace it with \(\displaystyle{{m}\choose{m}}=1\), and we have $${{n+1}\choose{m+1}}={{n}\choose{m}}+{{n-1}\choose{m}}+\dots+{{m+1}\choose{m}}+{{m}\choose{m}}$$ which was our goal.