Have you ever wondered how to add, subtract, multiply, and divide using Roman numerals? On one hand, we’ll give the simple answer that the Romans didn’t actually do what you think; on the other hand, we’ll consider what they actually did.
Adding and subtracting
We’ll start with a question from 1999:
Adding and Subtracting Roman Numerals I would like to know how to add and subtract Roman Numerals without converting them to regular numbers. I tried looking for patterns in different problems like XXX + X = XXXX, which I know is written XL. A problem I can't find a pattern for is LX - XIV = XLVI. What did the Romans do to solve this kind of problem?
Doctor Rick answered:
Hi, Greg. You might want to look at the Roman Numerals page in our Dr. Math FAQ: http://mathforum.org/dr.math/faq/faq.roman.html I have read that Europeans didn't switch to Hindu-Arabic numerals for a long time because they didn't see a reason to do arithmetic on paper, using written numerals. They would set up the numbers on an abacus, do the math, then write down the answer. (It's a little like using a calculator and not bothering to learn to do arithmetic by hand.) Roman numerals are closely related to the abacus -- that was one reason they liked them.
We discussed this relationship of Roman numerals to the abacus last time. The FAQ (before showing how to use the abacus!) gives two examples of how one might do addition, which I’ll reformat here for readability:
Let’s start with an addition problem: 23 + 58.
In Roman numerals, that’s XXIII + LVIII.
We’ll begin by writing the two numbers next to each other: XXIII LVIII.
Next, we rearrange the letters so that the numerals are in descending order: LXXVIIIIII.
Now we have six Is, so we’ll rewrite them as VI: LXXVVI.
The two Vs are the same as an X, so we simplify again and get LXXXI, or 81, as our final answer.
Note that this had no subtractive parts, so the sum is just the sum of all the symbols, which we could rearrange at will. All the work was mere simplification.
Now let’s try another addition problem:
14 + 17, or XIV + XVII.
Notice that the I in XIV is being subtracted, so this problem is going to be a little more complicated.
We begin the way we did before, by writing the numbers side by side: XIV XVII.
The subtracted I in XIV cancels out another I, so we cross them both out: X
IV XVII.Next we put the remaining letters into the right order: XXVVI. Simplifying gives us XXXI, or 31.
Would you enjoy doing this? Doctor Rick showed a subtraction, offering some ways to make both addition and subtraction easier:
If you want to add and subtract Roman numerals, I suggest you do a little bit of conversion first: get rid of the subtraction rule. That is, rewrite XIV as XIIII. Then you can subtract like this:
LX = XXXXX V IIIII
- XIIII = - X IIII
-------- -------------
XXXX V I
Now you can resume using the subtraction rule, so that the answer is XLVI.
I "borrowed" or "regrouped," sort of the way we do it in regular subtraction: I changed L into XXXXX so there would be enough X's, and I changed X into VV and one of the V's into IIIII so there would be enough I's. You can make shortcuts by remembering that V - IIII = I, for instance.
The Romans probably never wrote work like this, but did equivalent things on the abacus:
This method is much like using an abacus. The abacus does not use the subtraction rule; 4 (IV) is represented by four beads (like IIII). An abacus uses the same principle of changing a bead in one column into two "5" beads in the column to the right, then changing a "5" bead into five "1" beads in the same column. When it comes to multiplication, forget it! The Egyptians had a similar kind of numeral system (without the subtraction principle), and they used a completely different method of multiplication from ours -- one that works something like the way computers do it. You can find information on Egyptian multiplication by searching our Dr. Math Web site.
We’ll be taking that advice soon! But first we’ll try other ways.
Adding on the Roman (and later) counting board
Here is what the FAQ shows for addition:
When they wanted to do complicated arithmetic problems, the Romans used a special counting board or an abacus. A Roman counting board looked something like this:Counters, such as pebbles, were placed in each column. The columns were often grooved, so that the pebbles wouldn't roll away. A pebble in the bottom half of the board meant one, ten, one hundred, or one thousand, depending on its placement. A pebble in the top half had its value multiplied by five. For example, here's 2564 (MMDLXIV) on the counting board. Note that the Romans didn't worry about the subtraction principle unless they were actually writing their numbers down (and not always then).
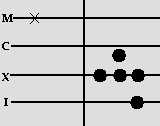
There were many variations on the Roman counting board, such as extra columns for larger numbers. People in the Middle Ages turned the columns the other way and drew lines down the middle, so that the board could hold several numbers at once. This board was designed for flat counters. Counters were placed on the line for I, X, C, and M, and between lines for V, L, and D. The little x on the M line is like the modern comma in 1,000: it helps you remember the meaning of each numeral's position. Let's use this board to add 23 and 58.
The first step is to place the two numbers (XXIII and LVIII) on the board:
Next, we slide the counters together:
We can replace five of the counters on the I line by a counter in the V space,
and the two counters in the V space by another counter on the X line, for a final answer of LXXXI.
It’s not hard to see how to follow the same procedure on the Roman version of the board, or on the abacus (which has attached beads or buttons rather than pebbles or counters). Here is a picture, from last time, of a replica abacus:

Multiplying?
Here’s a question from a teacher in 2001, which is not about Roman numerals at all, but will lead to them:
Place Value and Roman Numerals What is the importance of place value in relation to the value of a number? For example, where the number "2" is located in a number changes its valuation in the number, so how does one explain the importance of the place value in our number system? I have explored the realm of whole numbers, prime numbers, decimals, fractions, and mixed numbers, but cannot find anywhere to date, a cogent and readily ascertainable description or explanation of this phenomenon. Please explain so that I can address this problem with my class, as I cannot seem to describe this relation.
I answered:
Hi, James.
The way to demonstrate the importance of place value is to demonstrate how to multiply two Roman numerals.
You will quickly find that you have to learn the same facts in several different guises. For example, rather than just learning that 3 x 4 = 12, you have to learn
III x IV = XII
XXX x IV = CXX
CCC x IV = MCC
Because Roman numerals have no place value, when you do the same thing in different digits, you have to say it different ways. With place value, you can continue this with numbers as large as you wish, just reusing the same ten symbols; Roman numerals stop at the thousands, because they would need two new symbols for every new decimal place you tack on.
So the Romans, if they tried to multiply as we do, would have needed to memorize huge multiplication tables. That’s why they considered the very idea ridiculous.
Multiplying on the abacus
The FAQ. after showing how to add on the Roman counting board, shows how to use it to multiply.
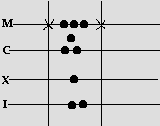
Here's an example of multiplication. We'll multiply 116 by 32 (CXVI times XXXII). This board has space for three numbers, so we can keep track of partial results.We have to break the multiplication into steps. 32 = 30 + 2, so we're going to start by multiplying by 30. The first step is to make a copy of the bigger number, 116, on the other side of the board.
Next we multiply our copy by 10, because 30 = 10*3. We can do this by sliding the counters up one full line.
Now we have to multiply by 3: just triple the number of counters in the copy.
We simplify our result, and remove the three X counters from the 32 section, to show that we have multiplied by 30.
The next step is to multiply 116 by 2. We can do this by doubling the counters for 116 on the left-hand side of the board.
We simplify again, and remove the 2 I counters, because we have finished multiplying by 2.
As soon as we push the counters together, and simplify one last time, we are done. Our answer is MMMDCCXII, or 3712. This can be checked using a calculator, or by hand.
I imagine you still prefer the modern way, whether on paper or with a calculator!
Multiplying the Egyptian way
As mentioned before, the Romans likely also used the Egyptian method, which is the subject of this 1996 question:
Egyptian Method of Multiplication Have you ever heard of an Egyptian Method of Multiplication?
Doctor Jodi answered:
Hi Carrie! Yes, we have.... Here's a description of the method, from http://www-groups.dcs.st-andrews.ac.uk/~history/HistTopics/Babylonian_and_Egyptian.html Unlike the Greeks, who thought abstractly about mathematical ideas, the Egyptians were only concerned with practical arithmetic. In fact the Egyptians probably did not think of numbers as abstract quantities, but always thought of a specific collection of 8 objects when 8 was mentioned. To overcome the deficiencies of their system of numerals the Egyptians devised cunning ways around the fact that their numbers were unsuitable for multiplication, as is shown in the Rhind papyrus which date from about 1700 BC.
All of this is true of the Romans, too!
The Rhind papyrus recommends that multiplication be done in the following way. Assume that we want to multiply 41 by 59. Take 59 and add it to itself, then add the answer to itself and continue:
41 59
______________
1 59
2 118
4 236
8 472
16 944
32 1888
______________
Since 64 > 41, there is no need to go beyond the 32 entry. Now go through a number of subtractions:
41 - 32 = 9, 9 - 8 = 1, 1 - 1 = 0
to see that 41 = 32 + 8 + 1.
All the arithmetic you need is doubling, in each column, and then subtraction to find which doubles add up to our multiplier!
Next check the numbers in the righthand column corresponding to 32, 8, 1 and add them.
59
______________
1 59 X
2 118
4 236
8 472 X
16 944
32 1888 X
______________
2419
Notice that the multiplication is achieved with only additions; notice also that this is a very early use of binary arithmetic.
We found that \(41=32+8+1\), so $$59\cdot41=59(32+8+1)\\=59\cdot32+59\cdot8+59\cdot\\=1888+472+59=2419$$
How is this binary? In splitting 41 into 32 + 8 + 1, we are effectively writing it as the binary number 101001. We’ll look at this more next week, in examining a related method in more depth.
It doesn’t matter which number you put on each column, though one way may involve more additions:
Reversing the factors we have
59 41
______________
1 41 X
2 82 X
4 16
8 328 X
16 656 X
32 1312 X
_______________
2419
Enjoy! Let us know if you need more help.
Here, \(58=32+16+8+2+1\), so $$41\cdot59=41(32+16+8+2+1)\\=41\cdot32+41\cdot16+41\cdot8+41\cdot2+41\cdot1\\=1312+656+328+82+41=2419$$
Dividing the Egyptian way
A 1998 question is about Egyptian division, which the Romans would also have used:
Egyptian Division My fourth graders are studying ancient Egypt. We have tried working with Egyptian multiplication but haven't found any reference to division. What format did the ancient Egyptians use for dividing? Can you help?
Doctor Mateo answered:
Hello Anne,
Egyptian division is basically Egyptian multiplication in reverse. The divisor is repeatedly doubled to give the dividend.
For example, 153 divided by 9.
powers of two divisor and successive doubling
(doubling)
2^0 = 1 9
2^1 = 2 18
2^2 = 4 36
2^3 = 8 72
2^4 = 16 144
2^5 = 32 288
288>153 so you can stop.
Look for the combination of numbers that add up to 153 in the divisor column.
This can be like a puzzle for the students and an excellent way to teach the problem-solving method known as guess and check.
The combination that works here is 144 + 9 since 144 + 9 = 153.
Here, rather than find which rows in the first column add up to the multiplier, we are finding which rows in the second column add up to the dividend.
To determine the divisor, look at the corresponding column of powers of two. Here we have:
2^4 corresponding with 144 and
2^0 corresponding with 9.
So the divisor is 2^4 + 2^0 = 16 + 1 = 17.
Here, we found that the dividend is $$153=144+9=9\cdot16+9\cdot1=9(16+1)=9\cdot17,$$ so \(153\div9=17\).
What if we didn’t get an exact sum to 153?
The complication with Egyptian division comes with remainders.
For example, 17 divided by 3.
Powers of two column divisor doubling column
2^0 = 1 3
2^1 = 2 6
2^2 = 4 12
2^3 = 8 24
24>17 so we can stop.
Looking at the combinations of 3, 6, and 12 we see that 12 + 3 = 15 is the closest we can seem to get without going over 17.
I’m going to skip the rest, because the Egyptians had their own way to handle fractions, which is irrelevant to Roman numerals. I imagine they would find a way to use uncia (twelfths).
Egyptian division in Roman numerals
We’ll close with a 2004 question on division:
Division with Roman Numerals I'm having real problems trying to divide using a non-place system. I can think in the Hindu place system, but the concept of using letters rather than numbers is confusing me. Can you please give me an example of a division calculation?
I answered:
Hi, Trish. There is a demonstration of addition and subtraction in our FAQ: Roman numerals http://mathforum.org/dr.math/faq/faq.roman.html That also points out that the Romans and others probably wouldn't have bothered doing arithmetic with their numerals in the sense we think of doing it; they would put the number on an abacus and use that. The Egyptians did multiplication and division using a method of doubling and halving, which is described here: Egyptian Method of Multiplication http://mathforum.org/library/drmath/view/57542.html Egyptian Division http://mathforum.org/library/drmath/view/57574.html Egyptian Division, Shelley Walsh http://faculty.ed.umuc.edu/~swalsh/Math%20Articles/EgyptDivide.html That method didn't require memorizing multiplication tables (which would have to be different from one place to another). Actually, the idea that one could memorize such tables was considered preposterous, at least for most people, long after Hindu-Arabic numerals became popular.
(The reference to halving is to a variant of the method, called Russian Peasant Multiplication; we’ll look into that next time.)
Each operation can in principle be done in any numeral system by thinking in terms of place value. For example, to add CIV and CCXCII, you would arrange each number in columns (as on an abacus, or in a place-value system) and add the columns:
C IV
+ CC XC II
----------
CCC XC VI
I can see why division would be the hardest to do this way; estimating a quotient requires some sort of familiarity with multiplication tables. Probably anything reasonable you do will amount to either translating (bit by bit) into Hindu-Arabic, or thinking in terms of an abacus, or using the Egyptian method. We could try to demonstrate several such techniques, but you get the idea: if you want to do as the Romans did, you won't bother!
But what would it look like to use the Egyptian method for division, using Roman numerals? Let’s have fun!
I'll just try the Egyptian division using Roman numerals, since you asked for a sample. Here is 153 / 9, as in the link above:
I | IX * C L III X VI
II | XVIII -C XL IV + I
IV | XXXVI --------- ------
VIII | LXXII IX X VII
XVI | CXLIV*
I doubled starting at I and at IX until the next doubling would take me past CLIII; then subtracted each number in the second column that I could, marking those I used with *; then added the corresponding numbers in the first column to get my answer, XVII.
I have doubled repeatedly, starting with 1 and 9, then subtracted repeatedly from 153 to find that \(153=144+9\), just as in the example above. The doubling, and the subtractions, would undoubtedly be done on an abacus. I also suspect that they would skip the subtractive notation, and just write IIII and CXXXXIIII rather than IV and CXLIV. That takes less thought.

While reading the posting above, I noticed a couple errors in multiplication:
XXX x XV = CXX
CCC x CD = MCC
In the first of those lines, I think you meant to write XL (40) instead of XV (15), but that would still give a result off by a factor of ten: 30 times 40 is 1200, not 120. In the second line, 300 times 400 is 120,000, not 1200.
You missed a worse typo just before those: 3 x 4 = 13! Clearly they are meant to be versions of 3 x 4 = 12; I’ve fixed them so the second number in each case is IV = 4, not XV or CD.
Thanks for the catch (after 23 years).