(A new problem of the week)
We usually look here at problems or concepts that are relatively basic and generally applicable; that could give a wrong impression of the kinds of questions we get. Here I want to show a recent example of a discussion about a problem, related to a geometric figure called the arbelos, that is challenging though it does not require advanced knowledge. This illustrates how an interesting problem can stimulate thought and discussion beyond just solving it, and how a mix of individual problem-solving effort and research of known work can be illuminating.
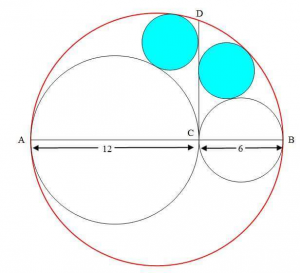
Here is the question, from earlier this month:
Find the distance between the centres of blue circles.
Doctor Rick, as usual, asked to see Suyash’s work and ideas, in order to know what sort of help he needs; our goal is to help students be able to solve problems themselves, not just to give answers. He added,
In particular, I have no idea what sort of math you have been learning. Personally, I would tackle this as an analytic-geometry problem, defining a coordinate system (perhaps with the origin at the center of the large circle) and writing a set of equations to be solved for the radii and the coordinates of the centers of the two smaller circles. This might get a bit tedious, but it should be straight-forward and surely will work. Is that something you’d do, or do you think another method would be expected?
I find this to be a good way to start an interaction, giving some ideas while waiting for details from the student. Suyash responded,
Thanks for your help sir. Now I have solved this question by using simple geometry and Pythagoras Theorem. Thanks for replying. I appreciate it.
We could have left it at that, but the problem was too interesting! Doctor Rick, having worked on the problem while he waited, answered,
If you constructed lines parallel to the lines in the figure in order to apply the Pythagorean theorem, your classical geometrical solution may have been essentially the same as the analytic-geometry approach I mentioned. If your approach didn’t involve finding the distances of the centers of the two small circles from the horizontal and vertical lines, then you may have a much nicer solution, and I’d be interested to see it. The fact that the two circles have the same radius, and that it is a very simple number, suggests that there may be an elegant solution.
He was doing something we recommend to students who want to get the most out of a problem: looking back after solving it, to see if there is a nicer alternative method. When an answer is simpler than the method of solution, it often suggests that there is more to learn! Suyash was willing to continue the discussion:
Here’s my solution, we could also directly use distance formula to find the required solution instead of doing congruency.
(I did some extra processing on his photo, to make it easier to read.)
He has skipped some steps; this is really a summary of key steps in the work, so it takes a little work to follow what he is doing. This is a good time to practice reading math slowly, figuring out the reason for every symbol he writes! But it is very well written.
(If you need help understanding a step, feel free to write with a comment or question! There are several points that are worthy of discussion; one, the simplification of a nested radical near the bottom, will have to be a subject of a post soon.)
Doctor Rick responded with some comments:
Thanks, Suyash. That’s very good! I like the way you chose to solve a more general problem, with a and b rather than the specific numbers given. Because you did that, we have an answer to the question, “Is it just coincidence that the two circles have the same radius?” I notice that the formula you obtained can be expressed in the neat form
1/r = 1/a + 1/b
and the symmetry on interchange of a and b is sufficient to show that both circles have the same radius.
This elicited a further question — good math is always worth discussing!
Thanks a lot. I think it’s due to the symmetric formula which we obtained, expressed by you in a very neat manner i.e. whatever value of a and b we take, the radius of both circles remains the same. What’s your thought in this matter: can it be proved that both radius are same without finding the general formula? Thanks for your help I appreciate it.
Doctor Rick did a little research:
Hi, Suyash. I’d say that in order to prove that the radii are the same regardless of the location of C on the diameter AB, we need to define variables; the thing to be proved is inherently a generalization, so whatever we come up with is, in a sense, a “general formula”. Perhaps you mean, though, whether we can prove the result without algebra, in a way that the ancient Greeks might have done it?
Recalling that the shape of the region above semicircles AC and CB, and below semicircle AB, is called an Arbelos, I searched for figures like yours and discovered that what we’re talking about is Proposition 5 of the Book of Lemmas, attributed to Archimedes:
Proposition 5: Let AB be the diameter of a semicircle, C any point on AB, and CD perpendicular to it, and let semicircles be described within the first semicircle and having AC, CB as diameters. Then if two circles be drawn touching CD on different sides and each touching two of the semicircles, the circles so drawn will be equal.
So there must be a classical-style, non-algebraic proof of the theorem. I have seen the two equal circles referred to as “Archimedes’ Circles” or “Archimedes’ Twins”. I haven’t found a copy of the proof from the book yet, and I haven’t tried proving it myself in a more classical framework. Of course, the way they proved this might turn out to be equivalent to what we have done.
Subsequently,
I found an English translation of The Book of Lemmas online. It’s part of the complete works of Archimedes; Proposition V is on page 305:
The Works of Archimedes (Google Books)
I haven’t gone over the proof thoroughly, but you will see that the end of the proof says,
AC . CB = AB . HE
In like manner, if d is the diameter of the other circle, we can prove that
AC . CB = AB . d
Therefore d = HE and the circles are equal.
In other words, he derived the formula d = ab/(a + b), showing that it holds for both circles. He did essentially what we have done in broad outline, but he does not invoke the Pythagorean theorem at all. Interesting.
In the past, we have discussed the arbelos a couple times by name (and probably many other times without naming it):
Circles within a Circle Arbelos Construction
Suyash replied,
Well, thanks for illuminating me with the classical Archimedes circle. I really appreciate your efforts towards solving my each and every query. Seems like this case is closed now and we have done all the required work to find the solution of the problem. Well, thanks a lot for guiding and helping me throughout the course. I appreciate your effort and time and would share how helpful this site is. Cheers!
Doctor Rick said something that is true for all of us:
You’re welcome, Suyash. We put in extra effort because it’s fun! I learned some things in this process.


Hi
I have a question. Why AS^2=(a+b-r1)^2 ?
I’ve been wondering when someone would ask about these details. I probably should at least have provided a clearer picture and defined the points, as Suyash did not do. (Just as an equation should never be written without defining variables, a figure should not be drawn without defining the assumed relationships.)
Here is a better version of his figure:
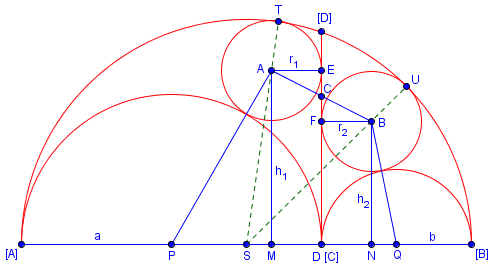
The point S is the center of the large semicircle, as P and Q are the centers of the smaller semicircles; so ST, as I’ve labeled it, is the radius, a+b, while AT is the radius r1. Therefore AS = ST – AT = a + b – r1.
Let me know if there are any other parts to be clarified.