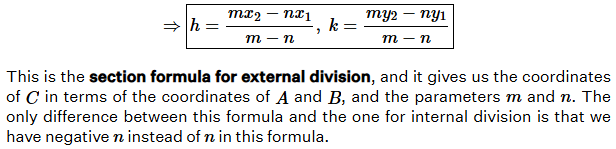Last time, we considered how to represent algebraically the division of a line segment in a given ratio. At the end, we touched on a subject I recalled discussing extensively almost four years ago: that such a “division” can be either internal (inside the segment, as you’d expect) or external (elsewhere on the line containing the segment). Let’s dive in.
Internal and external division
This question came from Rahul in October 2021:
Find the ratio in which P (8, 9) divides the segment joining A (1, -5) and B (2, -3). Also state the type of division and the order of the points.
I know that there are two types of division, Internal and External.
There are two formulas.
For internal division ((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n))
For external division ((mx2 – nx1)/(m – n), (my2 – ny1)/(m – n)).
I understand the derivation of these formulas also.
My question is,
While solving the problem which of the formulas is to be used?
How to guess whether the division is internal or external (without drawing the graph of this line)?
In the book they have directly used the internal division formula by assuming the ratio to be k:1 ( I understand m/n = (m/n)/1 = k/1, where k = m/n, I have no problem with this assumption of ratio.)
But then using the following formula (which looks like internal division),
8 = ((k)*(2) + (1)*(1))/(k+1),
they arrive at k = -7/6 and since the ratio is -ve and |-7/6| > 1 they say that the division is external and the order of the points is A-B-P.
Presumably, one is expected to answer the question without drawing a picture, but let’s draw it anyway:
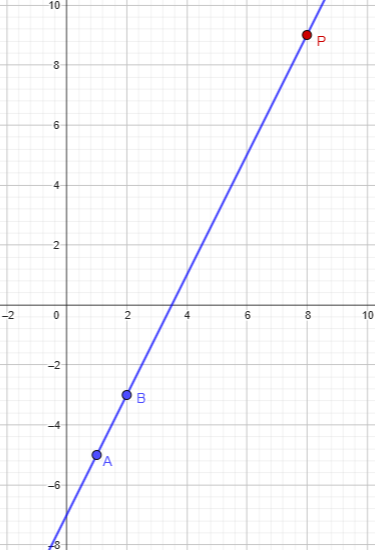
That definitely is not the kind of division we looked at last time (internal), for which we used Rahul’s first formula. In what sense can we even call this a division of AB, when the points are in the order A-B-P, with P on the outside?
If P were between A and B, then we would say we were dividing segment AB in the ratio AP : PB; here we’re just extending that definition. I think this is talked about less in America than in Rahul’s India, but it’s a perfectly valid concept. But it can get confusing.
The work he shows, from his book, starts with the internal division formula \(\displaystyle\left(\frac{mx_2 + nx_1}{m + n}, \frac{my_2 + ny_1}{m + n}\right)\), applied to the x-coordinate, taking the ratio to be \(m:n=k:1\), so that it becomes $$x=\frac{mx_2+nx_1}{m+n}\\8=\frac{k\cdot2+1\cdot1}{k+1}\\8=\frac{2k+1}{k+1}$$ Solving for k, $$8(k+1)=2k+1\\6k=-7\\k=\frac{-7}{6}$$ From this, they determine that the division is in fact external.
(Actually, we could just solve the general formula for k and get \(k=\frac{x-x_1}{x_2-x}\), which is just what we’d expect for internal division: the ratio of the first distance to the second distance. So none of this work is really needed! But then we wouldn’t have our interesting question …)
Rahul’s question is, why do they seem to just assume it’s internal, and then change their mind when they get a negative answer? Evidently this isn’t how the concept was presented!
How is the topic taught?
I answered:
You ask,
While solving the problem which of the formulas is to be used?
How to guess whether the division is internal or external (without drawing the graph of this line)?
There are a couple ways to answer this.
First, you can do what they do: Assume either type (I would probably use internal division as the default, just as they do), and if k is negative, you know it is actually external division. (More on this below.)
Second, you can look just at the x-coordinates, 8, 1, and 2. Since 8 is not between 1 and 2, P is not between A and B, so it will turn out to be external (and on the right, so the order is A-B-P).
If you fully understand the formulas
For internal division ((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n))
For external division ((mx2 – nx1)/(m – n), (my2 – ny1)/(m – n))
then you should have seen that the latter can be obtained from the former by replacing n with -n; that is, if k = m/n in the first formula is positive, the division is internal, and if it is negative, you get the second formula, with external division. To put it another way, there is really only one formula, and the sign of the ratio distinguishes internal from external. This is, in effect, what they did, even though they evidently teach two separate formulas.
This made me curious: Why would a textbook present these as two separate formulas? And is that standard? So I searched.
See, for example, here:
https://www.cuemath.com/geometry/external-division/
This treats the two formulas as distinct, but points out their relationship. I would think that your source would have made some such comment, since they are using this fact.
(Cuemath is based in India, but has international scope.)
Rahul later sent images of the textbook; here is the beginning of the section, showing that they do, to some extent, mention this:


It appears that they use the ratio sometimes to mean the ratio of signed lengths; yet when it is negative, they say it can be greater than 1, without using absolute value. And in the positive (internal) case, they use the odd symbol “\(\require{AMSsymbols}\gtrless\)”, which would appear to mean that the ratio must be either greater than or less than 1; but since it can in fact be equal to 1, I take it to mean “the ratio may be anything”. No wonder this is hard to follow.
At the end of the section, it says,

This suggests the correct ideas, but does not indicate using one formula for all cases, as they almost seem to have done (and as I will do).
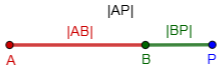
I myself would solve the problem not using memorized formulas, but by the kinds of thinking that could be used in deriving them. I might think in terms of vectors. Assuming external division (because I already know that it is), AP = kBP, so that
AB = AP – BP = kBP – BP = (k-1)BP,
so that k-1 is the ratio of (xB – xA) to (xP – xB).
Then if the y-coordinates agree, I have my answer. (If not, then the answer is that P does not lie on the line AB at all.)
The assumption of external division comes when I subtract \(AB=AP-BP\) rather than adding, \(AB=AP+PB\).
Searching for additional sources, I found this page (from Australia), which shows that the formula is easier to both state and derive in vector form:
https://www.maths.usyd.edu.au/u/MOW/vectors/vectors-5/v-5-1.html
This says,
On the next page, they extend this to the external case, stating that the same formula applies then with one of m and n being negative. The same derivation covers both cases.
Here they express the position vector of the dividing point \(R\) in terms of the position vectors of the given points \(P_1\) and \(P_2\). Note that the restriction, that \(m+n\ne0\), is not needed in the internal case, where everything is positive, but is needed when the same formula is used for external division, with a negative ratio:

Using the right formula gives the expected result
Rahul replied, trying to do the work with the opposite (correct) assumption:
I can assume either type.
So I assume external division.
The assumed ratio is k:1 only. The derivation of External division formula does not say any thing about the sign of the ratio; it is m/n only.
Then the point is 8 = ((k)*(2)-(1)*(1))/(k-1),
8 = (2k-1)/(k-1),
8k – 8 = 2k – 1
6k = 7
k = 7/6.
And due to the assumed external division I need not show the type of division depending on the sign of k (even if it is positive now).
Just because the ratio is > 1, I can say that the order of points is A-B-P (distance AP > distance PB).
I think I am still wrong somewhere .. or No?.
No, nothing is wrong.
The work he shows this time, parallel to the book’s, starts with the external division formula \(\left(\frac{mx_2-nx_1}{m – n}, \frac{my_2-ny_1}{m-n}\right)\), applied to the x-coordinate, taking the ratio to be \(m:n=k:1\), so that it becomes $$x_3=\frac{mx_2-nx_1}{m-n}\\8=\frac{k\cdot2-1\cdot1}{k-1}\\8=\frac{2k-1}{k-1}$$ Solving for k, $$8(k-1)=2k-1\\6k=7\\k=\frac{7}{6}$$ As we’ve seen, the only difference is the sign.
I answered:
When you use the formula for external division, the positive sign in your answer indicates that you chose correctly; it actually is external. Both formulas, as provided to you, assume numbers are positive.
The fact that the ratio you got is greater than 1 tells you that P is closer to B than to A, so that the order is A-B-P, which as we know is correct.
I see nothing wrong in your work or results, except for your implication that you can ignore the sign. It was important that it was positive.
What I said before is that the authors of the solution you showed appear to be aware that they can use either formula, and a negative k implies that they “used the wrong formula” and it is really the other type of division.
In my mind it would be far more sensible to talk about one formula (the internal one) with three cases:
k<-1 => external ABP;
-1<k<0 => external PAB;
k>0 => internal (P closer to A if k<1, closer to B if k>1).
Or something like that! But it seems, from my searching, that everyone who teaches any such formula teaches it as two separate formulas. It could be interesting to see how it was taught in your source.
We’ll see that these are correct.
He sent several pages from his textbook, which showed a geometrical derivation of the formulas that was not consistent in its use of signs, as we’ve seen; all of this is more easily done with vectors.
My version of the formulas and their proof
After a little more discussion, I spent a week writing up my own perspective on the formula(s):
What I want to do here is to write up how I would teach this topic if I were writing my own book. That means doing some research, which has taken time!
I have been trying to find more about the topic, particularly where it originated, and why the terminology is what it is. I feel as if I have read about it somewhere, perhaps in my reading in math history (it isn’t a standard topic in the U.S.), but most of the information I have found online is about current teaching of the topic, largely in India. Even Wikipedia has just a stub, with no history or explanation. A book of math tables I have includes the formula (called “point dividing P1P2 in ratio r/s”), under Analytic Geometry, with no mention of internal or external division.
I did find this concept in an old math dictionary I have, under the heading “Point of division”. Here is what it says, to give an example of American terminology and a slightly different perspective than what you have been given:
“The point which divides the line segment joining two given points in a given ratio. If the two given points have the Cartesian coordinates (x1, y1) and (x2, y2) and it is desired to find a point such that the distance from the first point to the new point, divided by the distance from the new point to the second point, is equal to r1/r2, the formulas giving the coordinates x and y of the desired point are x=[r2x1+r1x2]/[r1+r2], y=[r2y1+r1y2]/[r1+r2]. When r1/r2 is positive, the point of division lies between the two given points, and the division is said to be internal; the new point is said to divide the line segment internally in the ratio r1/r2. When this ratio is negative, the point of division must lie on the line segment extended, and it is then said to divide the line segment externally in the ratio |r1/r2|. …”
This agrees with me in thinking of this as one formula, not two, and fits the way the solution you quoted handles the negative ratio. It implicitly uses signed distances, without explanation.
We’ve already seen several variations of the concept and the formula. Note here that when the division is external, they use the absolute value of the ratio, though the ratio itself is negative. This is like saying, when an altitude is negative, that we are a positive number of meters below sea level: The negativity is in the word, rather than the number.
On the other hand, the way I naturally think of it, as I’ve mentioned, is best expressed in terms of vectors (which are equivalent to one-dimensional signed distances). I did find this very nice explanation of the whole topic from Australia, presented somewhat as I would want to (but without vectors).
So I’ll just write up my own explanation:
Dividing a segment: One dimension
Internal: A-P-B
We can start with the relatively natural concept of “internal division”; then we will find that we can extend it easily to “external division”, which on its face makes no sense (“cutting” a segment at a point outside the segment is an oxymoron!), but does make sense as an extension. After deriving the formula for the former, we will think about what would happen if the ratio were taken as negative (using the same formula).
We start with the basic idea of dividing a segment \(AB\) into two parts in a given ratio, in one dimension:
If, for example, we want the ratio \(AP:PB\) to be \(2:1\), then we know that \(P\) is \(\frac{2}{3}\) of the way from \(A\) to \(B\) (that is, \(\frac{2}{2+1}\)). So the distance \(AP\) is \(\frac{2}{3}\) of \(AB\), and \(P=A+\frac{2}{3}AB=2+\frac{2}{3}(5-2)=4\) in the example (where \(A=2\) and \(B=5\) as shown). And, indeed, \(AP=4-2=2\) and \(PB=5-4=1\), so the ratio \(AP:PB=2:1\) as desired.
In general, for a ratio \(m:n\), $$P=A+\frac{m}{m+n}(B-A)=\left(1-\frac{m}{m+n}\right)A+\frac{m}{m+n}B\\=\frac{n}{m+n}A+\frac{m}{m+n}B=\frac{nA+mB}{m+n}.$$ That is our formula, in the internal case, which is most natural.
External: A-B-P case
Now we might ask, what happens to the ratio if P is outside of the segment; or we might ask, what if we used a negative ratio? These are typical questions a mathematician asks, trying to extend an idea as far as it will go.
Let’s ask the former question: What if P is on the right (that is, beyond B)?
In this example, \(AP=6-2=4\) and \(PB=5-6=-1\), using signed distances on the number line. So we have \(AP:PB=4:-1\). And we can see in general that whenever \(P\) is outside of the segment (but still on the line \(AB\)), one of the signed distances \(AP\) and \(PB\) will be positive, and the other negative, so we have a negative ratio.
This motivates the idea that external division corresponds to a negative signed ratio \(AP:PB\).
Now suppose we are given such a negative ratio; we can do the same calculation as before: Given the ratio \(AP:PB=4:-1\), we see that since \(AB=AP+PB\), \(P\) will be \(\frac{4}{3}\) of the way from \(A\) to \(B\) (that is, \(\frac{4}{4+-1}\)). So the distance \(AP\) is \(\frac{4}{3}\) of \(AB\), and $$P=A+\frac{4}{3}AB=2+\frac{4}{3}(5-2)=6$$ as we see.
This is the very same calculation as before, but with a negative number; using the formula with \(m=4\) and \(n=-1\), we have $$\frac{nA+mB}{m+n}=\frac{-1(2)+4(5)}{4-1}=\frac{18}{3}=6.$$
Now, I happened to take m as positive and n as negative because I knew the result; if I knew only the ratio, I might just as well call it \(-4:1\). Would the formula still work? Yes:
Taking \(m=-4\) and \(n=1\), we have $$\frac{nA+mB}{m+n}=\frac{1(2)-4(5)}{-4+1}=\frac{-18}{-3}=6,$$
giving the same result as before. In fact, the formula can be simplified to use only the fraction \(\frac{m}{n}=k\), by dividing numerator and denominator by n: $$\frac{nA+mB}{m+n}=\frac{A+\frac{m}{n}B}{\frac{m}{n}+1}=\frac{A+kB}{k+1},$$ showing that only the sign of the ratio itself matters (not which term is negative).
The only odd thing there is that we can’t have \(AP=-4\) and \(PB=1\) if \(A\) is to the left of \(B\), because necessarily \(AB=AP+PB\), and \(-4+1=-3\), not \(3\). So this ratio would imply that \(B\) is to the left of \(A\).
External: P-A-B case
What if P is on the left?
Now, \(AP=-1\) and \(PB=4\), using signed distances on the number line. So we have \(AP:PB=-1:4\). Again we can do the calculation: the ratio \(AP:PB=-1:4\), so \(P\) is \(-\frac{1}{3}\) of the way from \(A\) to \(B\) (that is, \(\frac{-1}{-1+4}\)). So the distance \(AP\) is \(-\frac{1}{3}\) of \(AB\), and $$P=A+\left(-\frac{1}{3}\right)AB=2+\left(-\frac{1}{3}\right)(5-2)=1.$$
Again, using the formula with \(m=-1\) and \(n=4\), we have $$\frac{nA+mB}{m+n}=\frac{4(2)+(-1)(5)}{-1+4}=\frac{3}{3}=1.$$
So we have one formula that applies to all three cases (external P-A-B, internal A-P-B, and external A-B-P).
It’s also worth observing that none of what we’ve done depends on \(A\) being to the left of \(B\); all the directions (signs) will just change.
One remaining question is, what determines whether P is on the left or the right? If we think about this, we see, first, that a positive ratio means internal division; and, second, that if \(P\) is to the right of the midpoint (that is, closer to \(B\) than to \(A\)), then \(|AP|>|PB|\), so \(|AP/PB|>1\). So
- if \(k>0\), we have A-P-B;
- if \(k<-1\), we have A-B-P; and
- if \(-1<k<0\), we have P-A-B.
Here are locations of \(P\) corresponding to varying values of k:
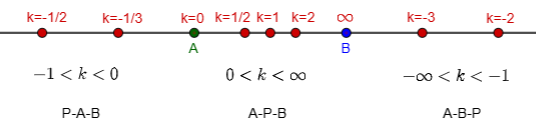
The point at infinity corresponds to \(k=-1\).
Dividing a segment: Two dimensions
Moving to the two-dimensional case (which can easily be extended to three dimensions), I’ll first state the problem in terms of vectors and derive a single formula for the coordinates of P; then I’ll translate that into non-vector terms.
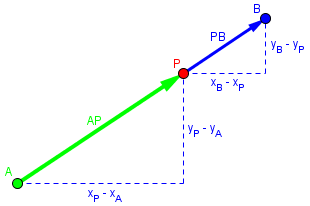
A point P on a line AB is said to divide segment AB in the ratio k = m/n if the signed distances AP and PB are in that ratio, so that, using vectors, AP = k PB. If k is positive, both vectors are in the same direction, as in the first picture here, so P is between A and B, and we say P divides AB internally. If k is negative, then the vectors are in opposite directions, so that P may be either beyond A, or beyond B, as shown in the second and third pictures later. In these cases, we say that P divides AB externally.
We will work from this drawing for the internal case (A-P-B), but it will become clear that, as long as we think in terms of signed distances, everything is still true in the other cases. It will also be clear that what is said does not depend on the fact that, in our picture, both the x- and y-coordinates of B are greater than those of A; in other cases, some of the numbers involved will simply be negative. (Incidentally, I believe this concept predates the concept of negative numbers, which is why internal and external division have traditionally been considered separately.)
I notice that I changed ratios like “k:1 = m:n” to fractional notation, \(k=\frac{m}{n}\), which to my mind is not ideal; I think of “part-to-part” ratios as conceptually different from fractions, which are “part-to-whole”, though mathematically almost equivalent. (See What is a Ratio, Really?) Please forgive me if this bothers you, too! But it makes several things easier.
We are given points A(xA, yA) and B(xB, yB), and we want a point P on the segment joining them, with |AP|/|PB| = k (= m/n). In terms of vectors, AP = k PB. Therefore
$$\overrightarrow{AB}=\overrightarrow{AP}+\overrightarrow{PB}=k\overrightarrow{PB}+\overrightarrow{PB}=(k+1)\overrightarrow{PB},$$ so that
$$\overrightarrow{PB}=\frac{1}{k+1}\overrightarrow{AB};$$ and
$$\overrightarrow{AP}=\overrightarrow{AB}-\overrightarrow{PB}=\overrightarrow{AB}-\frac{1}{k+1}\overrightarrow{AB}=\frac{k}{k+1}\overrightarrow{AB}.$$
Now, we can locate P by the position vector OP. We have
$$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}=\overrightarrow{OA}+\frac{k}{k+1}\overrightarrow{AB}\\=\overrightarrow{OA}+\frac{k}{k+1}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)\\=\overrightarrow{OA}+\frac{k}{k+1}\overrightarrow{OB}-\frac{k}{k+1}\overrightarrow{OA}\\=\frac{1}{k+1}\overrightarrow{OA}+\frac{k}{k+1}\overrightarrow{OB}=\frac{\overrightarrow{OA}+k\overrightarrow{OB}}{k+1}$$
This is the vector form of our formula, which in component form is
$$\left<\frac{x_A+kx_B}{k+1},\frac{y_A+ky_B}{k+1}\right>$$
Replacing k with m/n, when the ratio is a ratio of (signed) integers, this formula becomes
$$x=\frac{x_A+k x_B}{k+1}=\frac{x_A+\frac{m}{n}x_B}{\frac{m}{n}+1}=\frac{nx_A+mx_B}{m+n},$$
and similarly for y.
This is the formula as commonly taught.
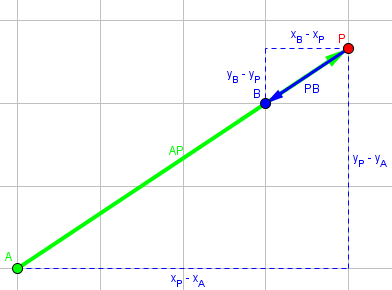
Now, none of this depended on the signs of k or of m and n, so the entire derivation still applies to this second case (A-B-P):
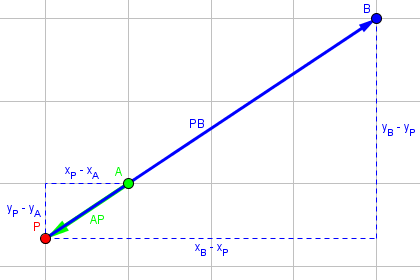
or to this third case (P-A-B):
In the former example, we might have A = (1, 1), B = (4, 3), and AP = -4 PB, so k = -4, or m = -4 and n = 1, so
$$P=\left(\frac{nx_A+mx_B}{m+n},\frac{ny_A+my_B}{m+n}\right)=\left(\frac{(1)(1)+(-4)(4)}{-4+1},\frac{(1)(1)+(-4)(3)}{-4+1}\right)=\left(5,3\frac{2}{3}\right)$$
In the latter example, AP = -1/4 PB, so k = -1/4, or m = -1 and n = 4, so
$$P=\left(\frac{nx_A+mx_B}{m+n},\frac{ny_A+my_B}{m+n}\right)=\left(\frac{(4)(1)+(-1)(4)}{-1+4},\frac{(4)(1)+(-1)(3)}{-1+4}\right)=\left(0,\frac{1}{3}\right)$$
That illustrates how we can apply the one formula in any case.
Weighted average
We can close with an alternative view of the problem, which I find more useful for many purposes. Observe that we can write the formula for x as \(\frac{1}{k+1}x_A+\frac{k}{k+1}x_B\) or as \(\frac{n}{m+n}x_A+\frac{m}{m+n}x_B\). In each case we have two coefficients whose sum is 1. If we let \(t=\frac{k}{k+1}=\frac{m}{m+n}\), then \(1-t=\frac{1}{k+1}=\frac{n}{m+n}\), so the formula simply says, \(x=(1-t)x_A+tx_B\).
This is simply a weighted average of A and B, with the weights being the terms m and n of the ratio. We are parametrizing the line using a parameter t such that t = 0 at A and t = 1 at B. We are dividing the segment internally when t is between 0 and 1.
And since \(k=\frac{t}{1-t}\), we find that internal division corresponds to positive k (because that is when both \(t\) and \(1-t\) are positive).
This is what we discussed last time in the internal case.