A couple recent questions asked what constitutes “standard form” for a quadratic equation; that will lead us to some older questions about “standard form” for a linear equation. We’ll see that “standard” isn’t quite as standard as you might think.
Standard form for a quadratic
The first question is from Charliemagne, a teacher (apparently in the Philippines), in June:
In teaching quadratic equations, I’ve always emphasized the standard form as: ax² + bx + c = 0, where a, b, and c are real numbers and a ≠ 0.
Now, I encountered a situation in class where the same quadratic equation was written in two different ways — both logically correct but structurally different.
For example, given: x² + 2x = -3
One student transposed all terms to the right side, resulting in: 0 = -x² – 2x – 3, which they rewrote as: -x² – 2x – 3 = 0 — a standard form with a negative leading and linear coefficient.
Another student transposed only the constant to the left side, resulting in: x² + 2x + 3 = 0 — a standard form with positive coefficients.
Both forms clearly preserve the equation’s roots. But my question is this:
From a pedagogical or mathematical convention perspective, should one of these be preferred as the “standard form,” or are both equally acceptable? And if both are valid, is it fair to say that any quadratic equation can have two possible standard forms — depending on how terms are transposed and the sign of a?
Thanks in advance!
The basic question here is, is there a unique “standard form” for any given quadratic equation, or can two different equations both be said to be “in standard form”? Given the definition at the start, the latter is clearly true. Is there more to it?
(By the way, I find that some sources call this the “general form”, as Charliemagne will later, and use “standard form” to refer to what is also called “vertex form”. This gets confusing! Also, quadratic equations don’t have to have real coefficients, but usually do in introductory classes.)
I answered:
Hi, Charliemagne.
I would say that standard form is just what is taught (everywhere I have looked), namely any polynomial written in descending order and set equal to 0. In fact, there are more than just two valid answers!
On the other hand, in practice, it is usually best to have a positive leading term, simply because that makes the work of solving easier, no matter what method you use (factoring, completing the square, quadratic formula). So I generally move all terms to whichever side will make a > 0 (or, equivalently, multiply by -1 if needed to accomplish that goal).
She actually didn’t mention descending order as a requirement; I’ve added that. But even so, “standard form” covers more than just one way to write a particular equation.
So, given the equation \(x^2+2x=-3\), I would choose to move everything to the left side, where the leading term would be positive: $$x^2+2x+3=0.$$ And given \(3=2x+x^2\), I would move everything to the right side, for the same reason, and then flip it around to the usual order: $$3=2x+x^2\\0=x^2+2x-3\\x^2+2x-3=0.$$
In fact, have you noticed that your equation is also equivalent to 3x2 + 6x + 9 = 0, or 1/2 x2+ x + 3/2 = 0, which are also in standard form? The definition of standard form does not require that it be in lowest terms (no common factor), or even integer coefficients — indeed, it can’t, because some quadratic equations can’t be written in that form, such as (to take it to an extreme) πx2 – 2x + √3 = 0, with irrational coefficients, though your students will never see anything like that.
All of the equations mentioned here are in standard form; but only the first two can be rewritten further, to make them easier to work with: $$3x^2+6x+9=0\\\frac{3}{3}x^2+\frac{6}{3}x+\frac{9}{3}=0\\x^2+2x+3=0$$ and $$\frac{1}{2}x^2+x+\frac{3}{2}=0\\2\cdot\frac{1}{2}x^2+2\cdot x+2\cdot\frac{3}{2}=0\\x^2+2x+3=0$$
So all of these should be accepted if the problem specifically called for writing it in standard form; but if that is just a step in the process of solving, I would strongly recommend putting the equation in “nice standard form”, with a positive leading term, and all integer coefficients if possible, and would suggest dividing by a common factor, as a matter of wisdom rather than law. This just makes the next step easier.
Yes, I actually used the term “nice standard form” when I taught this! And I recommended it, without requiring it.
Ultimately, we see that there are two distinct issues: standard form means the general type of equation that is ready for the quadratic formula. (Other methods of solving call for different forms: completing the square requires the constant to be alone on the right, and factoring requires standard form with integer coefficients.)
But we can go beyond that to prepare for the next step, by simplifying the problem, if possible. But as I have often said, “Simplicity is in the eye of the beholder.” An equation is simple enough when it is good enough for the next thing you want to do. Most things I’d want to do would be easier to do with a positive leading coefficient, for example (including the quadratic formula, which gets riskier with a negative denominator). But if the next thing you want to do is just to submit it to a teacher, then “simple” is whatever the teacher asks for! We’ll see more about that later.
Incomplete and pure quadratics
The next day, Charliemagne asked about a further distinction:
I am seeking clarification on a topic that seems to have different interpretations across textbooks and resources. It concerns incomplete quadratic equations, sometimes referred to as “pure quadratics.”
We know that the general form of a quadratic equation is: ax² + bx + c = 0, where a ≠ 0.
Some sources define incomplete quadratic equations as those in which the linear term is missing, meaning b = 0. For example:
3x² + 5 = 0
However, other sources define incomplete quadratics more broadly—as any quadratic equation where either the linear term (b) or the constant term (c) is missing. For example:
4x² – 12x = 0 (c = 0)
x² = 0 (b = 0 and c = 0)
So my question is:
Which of these forms are formally considered “incomplete quadratic equations”?
Is there a widely accepted convention that restricts this term only to cases where b = 0, or are both forms (b = 0 or c = 0) considered incomplete?
If there are any formal definitions, textbooks, or standards you can refer me to, I’d really appreciate it.
Thank you in advance!
I myself was not familiar with this as a formal term, but it makes perfect sense as a descriptive term.
I answered:
Hi, Charliemagne.
I would naturally take “incomplete” to mean that not all three terms are present, so an equation would be an incomplete quadratic if either the linear term or the constant is missing. (It wouldn’t be quadratic without the quadratic term!)
Similarly, I would take “pure quadratic” to mean that there is no linear term, so that it has the form ax2 + c = 0. This would include the trivial case where both b and c are zero.
A Google search suggests that this is usual, among those who use the terms at all. (I don’t use them, because I don’t consider them important to define; if a term is missing, I just point out that it is easier to solve than the general case. Neither term is used in the textbook I last taught from.)
Where the term “incomplete quadratic” is used, as I find here, it is just to call attention to two or three special cases that are easier to solve. It is not a single case with a single method of solution, as one might expect. So they agree with me.
The term “pure quadratic” seems to be less common; here is one source, from India, which doesn’t use the word “incomplete” at all.
In fact, in Google Books, I find it mostly in old textbooks. Here is an example of old usage (Durell, 1915) where “incomplete” is a synonym for “pure”, just as Charliemagne indicated:

Here is another (Young and Jackson, 1908) where pure quadratics are just one kind of incomplete quadratic, which makes more sense to me:

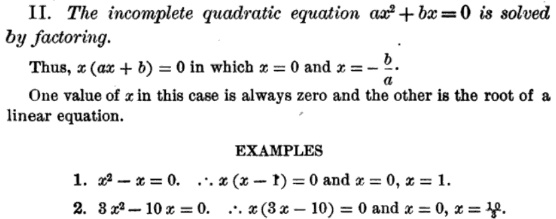
I was able to find one current book (which makes them synonyms):

Here is another, that distinguishes the two in a different way:

Here’s one more source I found (1999), with yet another use of these terms:

So, yes, the definitions do vary!
As to which are considered “incomplete quadratic equations”, I would say that 4x2 – 12x = 0, x2 = 0, and also x2 + 4 = 0, with b=0, are incomplete. Each is missing at least one non-quadratic term.
These are the three types of incomplete quadratic equation, respectively \(ax^2+bx=0\), \(ax^2=0\), and \(ax^2+c=0\).
I see no reason to say that 4x2 – 12x = 0 is not incomplete. Wouldn’t that mean that it is complete? Clearly “complete” should mean that all terms are present.
But again, I don’t think of these as important terms to define. For example, Wikipedia does not use these terms.
It does make sense to identify pure quadratic equations, ax2 + c = 0, which can be solved by isolating the square and taking the square root. (And this form is the goal of completing the square!)
It could also be useful to point out that when c = 0, ax2 + bx = 0, factoring is easy (x is a common factor), so noticing that is useful, but you don’t mention a name being given just for this case, and I can’t think of one! The main reason for pointing out this case is that students too often confuse it with the pure quadratic case, and factor it incorrectly. (I would often include one like this in tests, wanting to be kind, only to discover that some students misread it.)
Again, I see no reason to give a name to incomplete quadratics in general, as that doesn’t help in solving them.
But if the term is used, it makes sense to use it in the broad sense.
Standard form for linear equations
Looking back, I find a question from November, 2023 about the same idea in linear equations:
Hi Dr Math,
I was reading from a math book for intermediate stage, and I read this definition “Ax + By = C is the standard form of the linear equation in two variables, such that A ≥ 0. A, B ≠ 0 at the same time, A, B, C are integers, and the g.c.d. for them is 1.”
Is this definition correct?
Note that this is an equation in two variables, not one variable as in the quadratic case; yet the ideas are very similar. We have a basic form (\(Ax+By=C\)), and additional requirements (on signs and integers and common factors). Is it all needed?
I answered:
Hi, Amia.
Yes, sort of.
The word “standard” is one of the least standard terms in mathematics! Its meaning varies a lot.
Many sources do use the word for the form “Ax + By = C”, or something similar (like Ax + By + C = 0). Some call this the “general form”. Its main benefit is that any line can be written in this form, even if it is vertical.
It is necessary that A and B not be both zero, or the equation would be satisfied by no points, or by all points in the plane.
The extra conditions in your version, that A ≥ 0, and that A, B, and C are integers with gcd 1, are appropriate if you want to have a single correct equation for a teacher to check. (This might be called the simplified standard form.)
Equations like \(0x+0y=0\) or \(0x+0y=1\) are not linear equations; the former is true of all points, and the latter of none. But must we reject, say, \(-2x+3y=5\), or \(4x-6y=-10\), or \(\frac{1}{3}x-\frac{1}{2}y=-\frac{5}{6}\)? (They are all equivalent.)
But in making these restrictions, you lose the main reason for the form: Not all lines can be written in that form, because not all lines have slope and intercepts that are all rational.
So this can be appropriate for classroom use when a teacher promises that all lines used in the class can be written in this form, but it is not universal. The rule would be utterly inappropriate in the real world. I see some sources including some or all of these restrictions, but most do not.
For example, with the added restrictions, the equation \(\pi x+2y=\sqrt{3}\) can’t be put into standard form, because we can’t have integer coefficients!
Here is one site I found that says it correctly:
This is exactly how I would say it.
As another example, a Google AI summary told me this (my highlights for emphasis) when I searched for “standard form of a linear equation”:

I agree.
Are there infinitely many correct answers?
This question has also been asked and answered on the old Ask Dr. Math site. Here is one such question, from a teacher in 2005:
Standard Form of a Line (Ax + By = C) In the standard form of a linear equation, Ax + By = C, what conditions do A, B, and C have to meet? Do you always have to have a positive integer for A? Do you have to have all the common factors of A, B, and C factored out? We know that A, B, and C should be integers according to our textbook definition. The textbook also gives all answers beginning with a positive A. Is this a standard way to write it, or just a preference of our book editors? We had a problem that worked out to .6x - y = 2.4. One student multiplied by 10 to get 6x - 10y = 24. Another used the fraction for .6 (3/5) and multiplied by 5 to get 3x - 5y = 12. I know they're equivalent equations, but are they both considered correct? Why doesn't our book say that you must have factored out the terms so you have the lowest values of A, B, and C? I hate to think I have to consider the infinite possibilities each time I check a paper.
Evidently this book includes integer coefficients as part of the definition, and implies more. What’s a teacher to do?
Doctor Rick answered:
Hi, Kelly. If your textbook says that A, B, and C must be integers, it is wrong! If that were so, the standard form Ax + By = C could not represent any line with irrational slope, or with an x- or y-intercept incommensurate with the slope. How would you put this equation into that form? y = pi*x - sqrt(2) The advantage of the standard form is that, unlike slope-intercept form for example, it can be used to represent *any* line. I wouldn't want to limit it by requiring A, B, and C to be integers!
Part of the meaning of “standard” is that, unlike the slope-intercept form, it applies to all lines, even vertical ones. This would not be a good idea. But …
What I've said so far is math. The rest is pedagogy. Your last sentence says it all: "I hate to think I have to consider the infinite possibilities each time I check a paper." The convenience of the teacher (or perhaps another reader of a paper) is the only reason to put restrictions on A, B, and C. In practice most, if not all, of the problems presented to the students will involve rational numbers, so it will in fact be possible to make A, B, and C integers. I think it is quite reasonable to require this, and in addition that A be positive and that A, B, and C be relatively prime. This reduces the infinite possibilities to exactly one, and indeed makes your work easier. I'm all for that! I only ask that you make clear to the students that this is to help you, and not because math requires it. Maybe you could even drive this home to them by removing the restrictions for one assignment-- and having them grade one another's papers!
The extra conditions are not part of the meaning of standard form; they are requests from the teacher, for her convenience!
Why do I have to make the x term positive?
We’ll close with one more, from a student in 2007:
Standard Form Equation of a Line Why is it that in an equation of a line, the x can never be a negative? For example, -2x - y + 3 = 0 must always be 2x + y - 3 = 0. Why do we need to make the x term positive? Thanks in advance...
This time the positive leading coefficient appears to have been taught as a requirement. (What about a horizontal line like \(2y=3\), with a zero coefficient of x?)
I answered:
Hi, Pao. It isn't really true: -2x - y + 3 = 0 is a perfectly good equation of a line. You don't HAVE to make the coefficient of x positive. But it makes some sense to define the STANDARD FORM of a line with that requirement; a standard form is sort of like a police mug shot, where they make everyone stand facing the same way so all the pictures can be easily compared. If nothing else, it makes it really easy for you or a teacher to check your answer by comparing it to the one correct answer. It doesn't really matter whether they face right or left, or whether we write the equation as Ax + By + C = 0 with A positive, or as C + By + Ax = 0 with C required to be positive. We just choose one form as the "standard" (which, by the way, differs a bit from book to book) and stick with that.
I often find students thinking that their answer to a problem is wrong because the back of the book shows a different form. Knowing what form they will use can help you write yours so it will match!
In the same way, some texts require that, IF the coefficients are all rational, you should always multiply by the LCD so that the coefficients are all integers and have no common factor. That is equivalent to asking students to write all fractions in lowest terms-- other forms have the same value, but this is easy to work with and easy to compare.
Basically, it’s just a good habit to develop.
In both cases, the ultimate reason is that you can multiply an equation by any constant, and the result will be an equivalent equation. In order to ensure that there is only one "correct" form, we make a restriction that can always be met by doing such a multiplication. (By the way, if any coefficients are irrational, or if the coefficient of x is zero, these rules CAN'T be followed, so you need some extra rules to cover those cases!)
I closed with a reference to Doctor Rick’s answer above.
For more about this form, see
Standard Form of a Line

